
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по муниципальному праву
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Дипломная работа: Использование информационных технологий в обучении информационному моделированию учащихся старших классов в рамках элективного курса информатики
Дипломная работа: Использование информационных технологий в обучении информационному моделированию учащихся старших классов в рамках элективного курса информатики
Дипломная работа
По теме: Использование информационных технологий в обучении информационному моделированию учащихся старших классов в рамках элективного курса информатики.
Содержание
информатика математическое моделирование
Введение
Глава 1. Теоретические основы информационного математического моделирования
§ 1.1 Анализ понятий, связанных с математическим моделированием
§ 1.2 Информационное математическое моделирование: понятие,
цели и этапы
§ 1.3 Различные классификации математических моделей
Глава 2. Методические аспекты обучения информационному моделированию учащихся старших классов в рамках элективного курса информатики
§ 2.1 Психолого-педагогическая характеристика учащихся старших классов
§ 2.2 Информационные технологии в обучении
§ 2.3 Анализ подходов к обучению информационному моделированию в школьном курсе информатики
§ 2.4 Формы и методы обучения информационному моделированию
§ 2.5 Элективные курсы в профильном обучении
Глава 3. Разработка элективного курса "Компьютерное математическое моделирование"
§ 3.1 Содержание и педагогические задачи обучения элективному курсу «Компьютерное математическое моделирование»
Введение
В настоящее время главное направление модернизации Российского образования обеспечить его новое качество. Это можно сделать, в том числе и совершенствуя методическую систему обучения включением актуального содержания и использованием современных средств обучения.
Человечество в своей деятельности постоянно создает и использует модели окружающего мира. Наглядные модели часто используются в процессе обучения. Применение компьютера в качестве нового динамичного, развивающего средства обучения — главная отличительная особенность компьютерного моделирования.
Курс "Основы информатики и вычислительной техники", введенный в отечественной школе в 1985 г., занял достойное место в системе общего образования (отметим, что его первоначальное название все чаще трансформируется в просто "Информатика", которое ниже и используется). Курс трижды изменял свое название и сейчас это «Информатика и ИКТ». В качестве одной из целей курса выступает формирование информационной культуры учащихся.
Анализу общеобразовательного значения информатики, отбору учебного материала для этой дисциплины посвящены исследования А.П.Ершова, В.Г.Житомирского, А.Г.Гейна, В.А.Каймила, А.А.Кузнецова, М.П.Лапчика, А.Г.Кушниренко, В.М.Монахова, С.А.Бешенкова, И.В.Роберт, И.Г.Семакина и др. Психолого-педагогическое обоснование использования компьютеров в учебном процессе проведено в работах Н.В.Апатовой, П.Я.Гальперина, Б.С.Гершунского, В.В.Давыдова, Е.И.Машбица, Н.Ф.Талызиной, Д.Ш.Матроса, И.В.Роберт, С.Г. Григорьева и др.
Поскольку ядро информатики образуется тремя взаимодополняемыми и относительно самостоятельными частями (по терминологии А.А.Дородницына): hardware (техническими средствами), software (программным обеспечением) и brainware (интеллектуальным обеспечением), - то курс информатики основной школы сочетает в себе введение в фундаментальные основы науки "Информатика" и ее пользовательскую компоненту. Для многих учащихся курс информатики на этом к заканчивается, но для значительной части средних школ (в частности, для всех специализированных по физико-математическому и естественнонаучному профилю), актуализируется вопрос о профильно-ориентированном продолжении подготовки по информатике и примыкающим к ней областям, требующим более специальных знаний. Такие направления уже складываются: программирование, вычислительная математика, информационное моделирование, компьютерная графика, компьютерные телекоммуникации, информационные системы и др.
Роль и место информационных систем, в понимании их как автоматизированных систем работы с информацией, в современном информационном обществе неуклонно возрастают. Методология и технологии их создания начинают играть роль, близкую к общенаучным подходам в познании и преобразовании окружающего мира. Это обусловливает необходимость формирования более полного представления о них не только средствами школьного курса информатики, но и при изучении других предметов, а также во внеклассной работе.
Вместе с тем, в силу сложности и объемности информационных систем, учащиеся не могут самостоятельно создавать их. Однако им вполне по силам создание моделей таких систем. При этом деятельность по созданию моделей информационных систем не только углубляет представление о них, но и способствует развитию интеллектуальных умений в области моделирования, позволяет развивать творческие способности учащихся.
Создание информационных систем, как и их моделирование, неизбежно сопровождается процессом их проектирования. Таким образом, моделирование информационных систем естественным путем связывается с использованием метода проектов в обучении.
Среди профильно-ориентированных курсов, продолжающих базовый курс информатики в старших классах полной средней школы, достойное место может занять курс "Компьютерное математическое моделирование" (КММ). Такой курс отличается значительной широтой, максимальным использованием межпредметных связей информатики, с одной стороны, и математики, физики, биологии, экономики и других наук, с другой стороны, причем связи эти базируются на хорошо апробированной методологии математического моделирования, которая делает предмет целостным. Метод математического моделирования является с давних времен одним из фундаментальных методов познания, а появление и развитие ИТ дало новый толчок его совершенствованию. Чтобы получить полноценное научное мировоззрение, развить свои творческие способности, учащиеся должны овладеть основами компьютерного математического моделирования, уметь применять полученные знания в учебной и профессиональной деятельности.
Таким образом, актуальность исследования очевидна.
Основной целью исследования является разработка и теоретическое обоснование содержания и методики обучения информатике в старших классах средней школы в условиях профильной дифференциации на примере курса "Компьютерное математическое моделирование".
Объектом исследования является процесс обучения информатике в старших классах средней школы в условиях введения профильного обучения.
Предмет исследования составляют принципы, содержание, организационные формы и методы профильного обучения информатике на примере элективного курса "Компьютерное математическое моделирование", основанного на изучении моделей из различных областей науки.
Рабочая гипотеза исследования заключается в том, что профильный курс "Компьютерное математическое моделирование" в старших классах средней школы выступает в качестве средства
•повышения интереса учащихся к математическим и естественнонаучным знаниям;
•усиления систематической подготовки учащихся по информатике и информационным технологиям;
• профессиональной ориентации учащихся.
Поставленная цель работы и выдвинутая нами гипотеза потребовали решения следующих конкретных задач:
• анализ понятий, связанных с компьютерным математическим моделированием;
• анализ структуры образовательной области "Информатика", выявление места курса "Компьютерное математическое моделирование" в этой образовательной области, выделение структурных элементов, которые составили бы разрабатываемый элективный курс;
• рассмотреть понятие и виды моделей в информатике;
• выделение основных знаний и умений, которыми должны овладеть учащиеся после изучения этого курса;
• рассмотреть особенности использования компьютерного моделирования при обучении учащихся решению планиметрических задач;
• разработка методики обучения проведению исследования объектов (процессов) с построением математической модели и дальнейшим компьютерным экспериментом;
• разработка учебно-методических материалов в помощь учителю.
Для решения сформулированных задач применялись такие методы исследования:
а) изучение и анализ философской, педагогической, дидактической, психологической, методической и специальной литературы по теме исследования;
б) анализ проектов образовательных стандартов, программ, учебных пособий и методической литературы по основам информатики и вычислительной техники и математике, смежным школьным предметам;
в) наблюдение за ходом учебного процесса, деятельностью учащихся, анкетирование, тестирование;
г) анализ преподавания основ информатики в школе;
д) педагогический эксперимент.
Теоретическое значение – данная работа вносит вклад в разработку теоретических и практических аспектов изучения использования информационных технологий в обучении информационному моделированию учащихся старших классов в рамках элективного курса информатики.
Практическая ценность состоит в том, что конкретный теоретический и практический материал может быть использован для лекций по методике преподавания информатики, математики и др. дисциплинам для учащихся старших классов.
Структура дипломной работы.
Дипломная работа состоит из введения, трех глав, заключения и списка литературы. Во введении обоснована актуальность проблемы исследования, сформулированы цель, объект, предмет, и задачи исследования. В первой главе рассматриваются теоретические основы информационного математического моделирования, во второй – методические аспекты обучения информационному моделированию учащихся старших классов в рамках элективного курса информатики, в третьей - дана разработка элективного курса «Компьютерное математическое моделирование». В заключении даны выводы и обобщения по теме. Список литературы состоит из 27 наименований.
Глава 1. Теоретические основы информационного математического моделирования
§ 1.1 Анализ понятий, связанных с математическим моделированием
Б.В.Бирюков, Ю.А. Гастеев отмечают, что моделирование представляет собой один из основных методов познания, является формой отражения действительности и заключается в выявлении или в воспроизведении тех или иных свойств реальных объектов, предметов и явлений с помощью других объектов, процессов, явлений, либо с помощью абстрактного описания в виде изображения, плана, карты, совокупности уравнений, алгоритмов и программ [2].
Возможности моделирования, то есть перенос результатов, полученных в ходе построения и исследования модели, на оригинал основаны на том, что модель в определенном смысле отображает (воспроизводит, моделирует, описывает, имитирует) некоторые интересующие исследователя черты объекта. Моделирование как форма отражения действительности широко распространено, и достаточно полная классификация возможных видов моделирования крайне затруднительна, хотя бы в силу многозначности понятия «модель», широко используемого не только в науке и технике, но и в искусстве, и в повседневной жизни.
Слово «модель» произошло от латинского слова «modulus», означает «мера», «образец». Его первоначальное значение было связано со строительным искусством и почти во всех европейских языках оно употреблялось для обозначения образа или прообраза, или вещи, сходной в каком-то отношении с другой вещью.
Моделирование в научных исследованиях стало применяться еще в глубокой древности и постепенно захватывало все новые области научных знаний: техническое конструирование, строительство и архитектуру, астрономию, физику, химию, биологию и, наконец, общественные науки. Большие успехи и признание практически во всех отраслях современной науки принес методу моделирования XX век. Однако методология моделирования долгое время развивалась отдельными науками независимо друг от друга. Отсутствовала единая системa понятий, единая терминология. Лишь постепенно стала осознаваться роль моделирования как универсального метода научного познания.
Термин «модель» широко используется различных сферах человеческой деятельности и имеет множество смысловых значений. В этом разделе мы будем рассматривать только такие модели, которые являются инструментами получения знаний.
Модель - это такой материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал так, что его непосредственное изучение дает новые знания об объекте-оригинале.
Под моделированием понимается процесс построения, изучения и применения моделей. Оно тесно связано с такими категориями, как абстракция, аналогия, гипотеза и др. Процесс моделирования обязательно включает и построение абстракций, и умозаключения по аналогии, и конструирование научных гипотез.
Главная особенность моделирования в том, что это метод опосредованного познания с помощью объектов-заместителей. Модель выступает как своеобразный инструмент познания, который исследователь ставит между собой и объектом, и с помощью которого изучает интересующий его объект. Именно эта особенность метода моделирования определяет специфические формы использования абстракций, аналогий, гипотез, других категорий и методов познания.
В самом общем случае при построении модели исследователь отбрасывает те характеристики, параметры объекта-оригинала, которые несущественны для изучения объекта. Выбор характеристик объекта-оригинала, которые при этом сохраняются и войдут в модель, определяется целями моделирования. Обычно такой процесс абстрагирования от несущественных параметров объекта называют формализацией. Более точно, формализация - это замена реального объекта или процесса его формальным описанием.
Основное требование, предъявляемое к моделям - это их адекватность реальным процессам или объектам, которые замещает модель.
Практически во всех науках о природе, живой и неживой, об обществе, построение и использование моделей является мощным орудием познания. Реальные объекты и процессы бывают столь многогранны и сложны, что лучшим (а иногда и единственным) способом их изучения часто является построение и исследование модели, отображающей лишь какую-то грань реальности и потому многократно более простой, чем эта реальность. Многовековой опыт развития науки доказал на практике плодотворность такого подхода. Более конкретно, необходимость использования метода моделирования определяется тем, что многие объекты (или проблемы, относящиеся к этим объектам) непосредственно исследовать или вовсе невозможно, или же это исследование требует слишком много времени и средств.
В моделировании есть два различных подхода. Модель может быть похожей копией объекта, выполненной из другого материала, в другом масштабе, с отсутствием ряда деталей. Например, это игрушечный кораблик, домик из кубиков, деревянная модель самолета в натуральную величину, используемая в авиа конструировании и др. Модели такого рода называют натурными.
Модель может, однако, отображать реальность более абстрактно - словесным описанием в свободной форме, описанием, формализованным по каким-то правилам, математическими соотношениями и т.п. Будем называть такие модели абстрактными.
Классификация абстрактных моделей:
1. Вербальные (текстовые) модели. Эти модели используют последовательности предложений на формализованных диалектах естественного языка для описания той или иной области действительности (примерами такого рода моделей являются милицейский протокол, правила дорожного движения).
2.
Математические модели - очень широкий класс
знаковых моделей (основанных на формальных языках над конечными алфавитами), использующих
те или иные математические методы. Например, математическая модель звезды будет
представлять собой сложную систему уравнений, описывающих физические процессы, происходящие
в
недрах звезды. Другой математической моделью являются, например, математические
соотношения, позволяющие рассчитывать оптимальный (наилучший с экономической точки
зрения) план работы какого-либо предприятия.
3. Информационные модели - класс знаковых моделей, описывающих информационные процессы (получение, передачу, обработку хранение и использование информации) в системах самой разнообразной природы. Примерами таких моделей могут служить OSI - семиуровневая модель взаимодействия открытых систем в компьютерных сетях или машина Тьюринга - универсальная алгоритмическая модель.
Подчеркнем, что граница между вербальными, математическими и информационными моделями может быть проведена весьма условно. Так, информационные модели иногда считают подклассом математических моделей. Однако, в рамках информатики как самостоятельной пауки, отделенной от математики, физики, лингвистики и других наук, выделение информационных моделей в отдельный класс является целесообразным. Информатика имеет самое непосредственное отношение и к математическим моделям, поскольку они являются основой применения компьютера при решении задач различной природы: математическая модель исследуемого процесса или явления на определенной стадии исследования преобразуется в компьютерную (вычислительную) модель, которая затем превращается в алгоритм и компьютерную программу,
Отметим, что существуют и иные подходы к классификации абстрактных моделей: общепринятая точка зрения здесь еще не установилась.
В прикладных науках различают следующие виды абстрактных моделей:
1. чисто аналитические математические модели, не использующие компьютерных средств;
2. информационные модели, имеющие приложения в информационных системах:
3. вербальные языковые модели;
4. компьютерные модели, которые могут использоваться для:
• численного математического моделирования;
• визуализации явлений и процессов (как для аналитических, так и для численных моделей);
• специализированных прикладных технологий, использующих компьютер (как правило, в режиме реального времени) в сочетании с измерительной аппаратурой, датчиками и т.п.
Большая часть данного курса связана с прикладными математическими моделями, в реализации которых используются компьютеры. Это вызвано тем, что внутри информатики именно компьютерное математическое и компьютерное информационное моделирование могут рассматриваться как ее составные части.
§ 1.2 Информационное математическое моделирование: понятие, цели и этапы
Начнем с термина «информация».
Во-первых, компьютер информацию в «сыром виде» не обрабатывает, и вообще, такого технического устройства нет.
Во- вторых, об алгоритмах обработки таких вещей можно говорить, лишь в каком-то переносном смысле.
И в-третьих, термин «информация», лишаясь при таком подходе каких-то границ, теряет свою познавательную ценность: его можно безболезненно опускать, он ничего не уточняет. Например, трава – это трава и становится она информационным объектом лишь в модельном построении после представления ее в виде текста.
Мы говорим «информация», когда нет нужды явно указывать на ее источник. Если мы говорим «информационная модель», то предполагаем наличие объекта, отражением которого служит модель, то есть отражение объекта средствами конечного алфавита называется его информационной моделью.
В некотором смысле любую информационную модель можно рассматривать как более или менее детализированное, так или иначе специализированное имя объекта. Однако принято именами называть лишь элементарные конструкции, тогда как более сложные называют информационными моделями.
Таким образом, обозначение, наименование объекта – это элементарная процедура, лежащая в основе информационного моделирования.
Информационное моделирование можно разделить на три типа.
Первый тип называется классификационным. На моделях этого типа, которые могут быть как дискретными, так и непрерывными, основана разработка данных, баз знаний, экспертных схем.
Второй тип называется динамическим, широко используется при компьютерном моделировании.
И, наконец, третий тип информационных моделей – языковой. Эти модели моделируют средства моделирования и являются по существу метамоделями [19].
Рассмотрим термин «компьютерная модель». В настоящее время под компьютерной моделью чаще всего понимают:
• условный образ объекта или некоторой системы объектов (или процессов), описанный с помощью взаимосвязанных компьютерных таблиц, блок-схем, диаграмм, графиков, рисунков, анимационных фрагментов, гипертекстов и т. д. и отображающий структуру и взаимосвязи между элементами объекта. Компьютерные модели такого вида мы будем называть структурно-функциональными;
• отдельную программу, совокупность программ, программный комплекс, позволяющий с помощью последовательности вычислений и графического отображения их результатов, воспроизводить (имитировать) процессы функционирования объекта, системы объектов при условии воздействия на объект различных, как правило случайных, факторов. Такие модели мы будем далее называть имитационными моделями.
Остановимся на информационных моделях, отражающих процессы возникновения, передачи, преобразования и использования информации в системах различной природы. Начнем с определения простейших понятий информационного моделирования.
Экземпляром будем называть представление предмета реального мира с помощью некоторого набора его характеристик, существенных для решения данной информационной задачи (служащей контекстом построения информационной модели). Множество экземпляров, имеющих одни и те же характеристики и подчиняющиеся одним и тем же правилам, называется объектом.
Таким образом, объект есть абстракция предметов реального мира, объединяемых общими характеристиками и поведением.
Информационная модель какой-либо реальной системы состоит из объектов. Каждый объект в модели должен быть обеспечен уникальным и значимым именем (а также идентификатором, служащим ключом для указания этого объекта, связи его с другими объектами модели). Таким образом обозначение, наименование объекта - это элементарная процедура, лежащая в основе информационного моделирования.
Объект представляет собой один типичный (но неопределенный) экземпляр чего-то в реальном мире и является простейшей информационной моделью. Объекты представляют некие “сущности” предметов реального мира, связанные с решаемой задачей.
Большинство объектов, с которыми приходится встречаться, относятся к одной из следующих категорий:
o реальные объекты;
o роли;
o события;
o взаимодействия;
o спецификации.
Реальный объект – это абстракция физически существующих предметов. Например, на автомобильном заводе это кузов автомобиля, двигатель, коробка передач; при перевозке грузов это контейнер, средство перевозки.
Роль – абстракция цели или назначения человека, части оборудования или учреждения (организации). Например, в университете как в учебном заведении это студент, преподаватель, декан; в университете как в учреждении это приемная комиссия, отдел кадров, бухгалтерия, деканат.
Событие – абстракция чего-то случившегося. Например, поступление заявления от абитуриента в приемную комиссию Университета, сдача (или несдача) экзамена.
Взаимодействия – объекты, получаемые из отношений между другими объектами. Например, сделка, контракт (договор) между двумя сторонами, свидетельство об образовании, выдаваемое учебным заведением его выпускнику.
Объекты-спецификации используются для представления правил, стандартов или критериев качества. Например, перечень знаний, умений и навыков выпускника математического факультета, рецепт проявления фотопленки.
Для каждого объекта должно существовать его описание – короткое информационное утверждение, позволяющее установить, является некоторый предмет экземпляром объекта или нет. Например, описание объекта “Абитуриент университета” может быть следующим: человек в возрасте до 35 лет, имеющий среднее образование, подавший в приемную комиссию документы и заявление о приеме.
Предметы реального мира имеют характеристики (такие, например, как имя, название, регистрационный номер, дата изготовления, вес и т.д.). Каждая отдельная характеристика, общая для всех возможных экземпляров объекта, называется атрибутом. Для каждого экземпляра атрибут принимает определенное значение. Так, объект Книга имеет атрибуты Автор, Название, Год издания. Число страниц.
У каждого объекта должен быть идентификатор – множество из одного или более атрибутов, значения которых определяют каждый экземпляр объекта. Для книги атрибуты Автор и Название совместно образуют идентификатор. В тоже время Год издания и Число страниц идентификаторами быть не могут – ни врозь, ни совместно, так как не определяют объект. Объект может иметь и несколько идентификаторов, каждый из которых составлен из одного или нескольких атрибутов. Один из них может быть выбран как привилегированный для соответствующей ситуации.
Объект может быть представлен вместе со своими атрибутами несколькими различными способами. Графически объект может быть изображен в виде рамки, содержащей имя объекта и имена атрибутов. Атрибуты, которые составляют привилегированный идентификатор объекта, могут быть выделены (например, символом * слева от имени атрибута):
В эквивалентном текстовом представлении это может иметь следующий вид:
Книга (Автор. Название. Год издания. Число страниц).
Привилегированный идентификатор подчеркивается.
Еще одним способом представления объекта информационной модели является таблица. В этой интерпретации каждый экземпляр объекта является строкой в таблице, а значения атрибутов, соответствующих каждому экземпляру, – клетками строки, табл. 1.
Таблица 1. Таблица как представление информационной модели
| Автор | Книга | ||
| Название | Год издания | Число страниц | |
|
Грин А. Стивенсон Р. П. Скотт В. Гончаров И. А. |
Бегущая по волнам Остров сокровищ Ричард Львиное Сердце Обрыв |
1988 1992 1993 1986 |
279 269 349 598 |
Можно классифицировать атрибуты по принадлежности к одному из трех различных типов:
• описательные;
• указывающие;
• вспомогательные.
Описательные атрибуты представляют факты, внутренне присущие каждому экземпляру объекта. Если значение описательного атрибута изменится, то это говорит о том, что некоторая характеристика экземпляра изменилась, но сам экземпляр остался прежним.
Указательные атрибуты могут использоваться как идентификаторы (или часть идентификаторов) экземпляра. Если значение указывающих атрибутов изменяется, то это говорит лишь о том, что новое имя дается тому же самому экземпляру.
Вспомогательные атрибуты используются для связи экземпляра одного объекта с экземпляром другого объекта.
Рассмотрим пример:
Автомобиль
гос. номер
марка
цвет
владелец
Атрибут “цвет” является описательным, атрибуты “гос. номер” и “марка” – указательными, атрибут “владелец” – вспомогательным, служащим для связи экземпляра объекта Автомобиль с экземпляром объекта Автолюбитель. Если значение вспомогательного атрибута изменится, это говорит о том, что теперь другие экземпляры объектов связаны между собой.
В реальном мире между предметами существуют различные отношения. Если предметы моделируются как объекты, то отношения, которые систематически возникают между различными видами объектов, отражаются в информационных моделях как связи. Каждая связь задается в модели определенным именем. Связь в графической форме представляется как линия между связанными объектами и обозначается идентификатором связи.
Существует три вида связи: один-к-одному (рис. 3), один-ко-многим (рис. 4) и многие-ко-многим (рис. 5).
Связь один-к-одному существует, когда один экземпляр одного объекта связан с единственным экземпляром другого. Связь один-к-одному обозначается стрелками и.
Связь один-ко-многим существует, когда один экземпляр первого объекта связан с одним (или более) экземпляром второго объекта, но каждый экземпляр второго объекта связан только с одним экземпляром первого. Множественность связи изображается двойной стрелкой.
Связь многие-ко-многим существует, когда один экземпляр первого объекта связан с одним или большим количеством экземпляров второго и каждый экземпляр второго связан с одним или многими экземплярами первого. Этот тип связи изображается двусторонней стрелкой. Помимо множественности, связи могут подразделяться на безусловные и условные. В безусловной связи для участия в ней требуется каждый экземпляр объекта. В условной связи принимают участие не все экземпляры объекта. Связь может быть условной как с одной, так и с обеих сторон.
Все связи в информационной модели требуют описания, которое, как минимум, включает:
• идентификатор связи;
• формулировку сущности связи;
• вид связи (ее множественность и условность);
• способ описания связи с помощью вспомогательных атрибутов объектов.
Дальнейшее развитие представлений информационного моделирования связано с развитием понятия связи, структур, ими образуемых, и задач, которые могут быть решены на этих структурах. Нам уже известна простая последовательная структура экземпляров – очередь. Возможными обобщениями информационных моделей являются циклическая структура, таблица.
Очень важную роль играет древовидная информационная модель, являющаяся одной из самых распространенных типов классификационных структур. Эта модель строится на основе связи, отражающей отношение части к целому: “А есть часть М” или “М управляет А”. Очевидно, древовидная связь является безусловной связью типа один-ко-многим и графически изображена на рис. 6, в. На этом же рисунке для сравнения приведены схемы информационных моделей типа “очередь” (а) и “цикл” (б).
Еще более общей информационной моделью является, так называемая, графовая структура, рис. 7. Графовые структуры являются основой решения огромного количества задач информационного моделирования.
Многие прикладные задачи информационного моделирования были поставлены и изучены достаточно давно, в 50-60-х годах, в связи с активно развивавшимися тогда исследованиями и разработками по научным основам управления в системах различной природы и в связи с попытками смоделировать с помощью компьютеров психическую деятельность человека при решении творческих интеллектуальных задач. Научное знание и модели, которые были получены в ходе решения этих задач, объединены в науке под названием “Кибернетика”, в рамках которой существует раздел “Исследования по искусственному интеллекту”.
Информационная модель типа “граф”
Итак, мы выяснили, что второй тип информационного моделирования – динамический, используется при компьютерном моделировании. Исторически случилось так, что первые работы по компьютерному моделированию, или, как говорили раньше, моделированию на ЭВМ, были связаны с физикой, где с помощью моделирования решался целый ряд задач гидравлики, фильтрации, теплопереноса и теплообмена, механики твердого тела и т. д. Моделирование в основном представляло собой решение сложных нелинейных задач математической физики с помощью итерационных схем, за исключением разве тех задач, где использовался метод Монте-Карло, и по существу было оно, конечно, моделированием математическим. Успехи математического моделирования в физике способствовали распространению его на задачи химии, электроэнергетики, биологии и некоторые другие дисциплины, причем схемы моделирования не слишком отличались друг от друга. Сложность решаемых на основе моделирования задач всегда ограничивалась лишь мощностью имеющихся ЭВМ.
Надо заметить, что подобный вид моделирования весьма широко распространен и в настоящее время. Более того, за время развития методов моделирования на ЭВМ при решении задач фундаментальных дисциплин и смежных предметных областей накоплены целые библиотеки подпрограмм и функций, облегчающих применение и расширяющих возможности моделирования. И все же в настоящее время понятие "компьютерное моделирование" обычно связывают не с фундаментальными дисциплинами, а в первую очередь с системным анализом - направлением кибернетики, впервые заявившим о себе в начале 50-х годов при исследовании сложных систем в биологии, макроэкономике, при создании автоматизированных экономико-организационных систем управления.
Компьютерное моделирование - метод решения задачи анализа или синтеза сложной системы на основе использования ее компьютерной модели. Суть компьютерного моделирования заключена в получении количественных и качественных результатов по имеющейся модели. Качественные выводы, получаемые по результатам анализа, позволяют обнаружить неизвестные ранее свойства сложной системы: ее структуру, динамику развития, устойчивость, целостность и др. Количественные выводы в основном носят характер прогноза некоторых будущих или объяснения прошлых значений переменных, характеризирующих систему.
Часто компьютерные модели проще и удобнее исследовать, они позволяют проводить вычислительные эксперименты, реальная постановка которых затруднена или может дать непредсказуемый результат. Логичность и формализованность компьютерных моделей позволяет выявить основные факторы, определяющие свойства изучаемых объектов, исследовать отклик физической системы на изменения ее параметров и начальных условий.
Компьютерное моделирование требует абстрагирования от конкретной природы явлений, построения сначала качественной, а затем и количественной модели. За этим следует проведение серии вычислительных экспериментов на компьютере, интерпретация результатов, сопоставление результатов моделирования с поведением исследуемого объекта, последующее уточнение модели и т.д.
К основным этапам компьютерного моделирования относятся: постановка задачи, определение объекта моделирования; разработка концептуальной модели, выявление основных элементов системы и элементарных актов взаимодействия; формализация, то есть переход к математической модели; создание алгоритма и написание программы; планирование и проведение компьютерных экспериментов; анализ и интерпретация результатов.
Различают аналитическое и имитационное моделирование. Аналитическими называются модели реального объекта, использующие алгебраические, дифференциальные и другие уравнения, а также предусматривающие осуществление однозначной вычислительной процедуры, приводящей к их точному решению. Имитационными называются математические модели, воспроизводящие алгоритм функционирования исследуемой системы путем последовательного выполнения большого количества элементарных операций.
А. Гультяев [6] отмечает, что принципы моделирования состоят в следующем:
1. Принцип информационной достаточности. При полном отсутствии
информации об объекте построить модель невозможно. При наличии полной
информации моделирование лишено смысла. Существует уровень информационной достаточности, при достижении которого может быть построена модель системы.
2. Принцип осуществимости. Создаваемая модель должна обеспечивать достижение поставленной цели исследования за конечное время.
3. Принцип множественности моделей. Любая конкретная модель отражает лишь
некоторые стороны реальной системы. Для полного исследования необходимо построить ряд моделей исследуемого процесса, причем каждая последующая модель должна уточнять предыдущую.
4. Принцип системности. Исследуемая система представима в виде совокупности взаимодействующих друг с другом подсистем, которые моделируются стандартными математическими методами. При этом свойства системы не являются суммой свойств ее элементов.
5. Принцип параметризации. Некоторые подсистемы моделируемой системы могут быть охарактеризованы единственным параметром: вектором, матрицей, графиком, формулой.
Компьютерное моделирование систем часто требует решения дифференциальных уравнений. Важным методом является метод сеток, включающий в себя метод конечных разностей Эйлера. Он состоит в том, что область непрерывного изменения одного или нескольких аргументов заменяют конечным множеством узлов, образующих одномерную или многомерную сетку, и работают с функцией дискретного аргумента, что позволяет приближенно вычислить производные и интегралы. При этом бесконечно малые приращения функции f = f(x, у, z, t) и приращения ее аргументов заменяются малыми, но конечными разностями.
Математическая модель выражает существенные черты объекта или процесса языком уравнений и других математических средств. Собственно говоря, сама математика обязана своим существованием тому, что она пытается отразить, т. е. промоделировать на своем специфическом языке закономерности окружающего мира. Огромный толчок развитию математического моделирования дало появление ЭВМ, хотя сам метод зародился одновременно с математикой тысячи лет назад.
Математическое моделирование как таковое отнюдь не всегда требует компьютерной поддержки. Каждый специалист, профессионально занимающийся математическим моделированием, делает все возможное для аналитического исследования модели. Аналитические решения (т. е. представленные формулами, выражающими результаты исследования через исходные данные) обычно удобнее и информативнее численных. Однако, возможности аналитических методов решения сложных математических задач очень ограничены и, как правило, эти методы гораздо сложнее численных. В нашем курсе доминируют численные методы, реализуемые на компьютерах. Отметим, что понятия «аналитическое решение» и «компьютерное решение» отнюдь не противостоят друг другу, так как
а) все чаще компьютеры при математическом моделировании используются не только для численных расчетов, но и для аналитических преобразований;
б) результат аналитического исследования математической модели часто выражен столь сложной формулой, что при взгляде на нее не складывается наглядного восприятия описываемого ею процесса. Эту формулу (хорошо еще, если просто формулу!) нужно протабулировать, представить графически, проиллюстрировать в динамике, иногда даже озвучить, т.е. проделать то, что называется «визуализацией». Очевидно, возможности современных компьютеров наилучшим образом соответствуют этой задаче.
Рассмотрим процесс компьютерного математического моделирования, включающий численный эксперимент с моделью (рис. 8).
Первый этап - определение целей моделирования. Основные из них таковы:
1) Понимание
Модель в этой ситуации нужна для того, чтобы понять, как устроен конкретный объект, какова его структура, основные свойства, законы развития и взаимодействия с окружающим миром.
2) Управление
Модель нужна для того, чтобы научиться управлять объектом (или процессом) и определить наилучшие способы управления при заданных целях и критериях;
3) Прогнозирование
Модель используется для того, чтобы прогнозировать прямые и косвенные последствия воздействия на объект заданными способами.
Поясним это на примерах. Пусть объект исследования - взаимодействие потока жидкости или газа с телом, являющимся для этого потока препятствием. Опыт показывает, что сила сопротивления потоку со стороны тела растет с ростом скорости потока, но при некоторой достаточно высокой скорости эта сила скачком уменьшается с тем, чтобы с дальнейшим увеличением скорости снова возрасти. Что же произошло, обусловив уменьшение силы сопротивления? Математическое моделирование позволяет получить четкий ответ: в момент скачкообразного уменьшения сопротивления вихри, образующиеся в потоке жидкости или газа позади обтекаемого тела, начинают отрываться от него и уноситься потоком.
Пример совсем из другой области: мирно сосуществовавшие со стабильными численностями популяции двух видов особей, имеющих общую кормовую базу, «вдруг» начинают резко менять численность - и здесь математическое моделирование позволяет (с известной долей достоверности) установить причину явления, или, по крайней мере, опровергнуть определенную гипотезу о его причинах.
Выработка концепции управления объектом - другая возможная цель моделирования. Какой режим полета самолета выбрать для того, чтобы полет был вполне безопасным и экономически наиболее выгодным? Как составить график выполнения сотен видов работ на строительстве большого объекта, чтобы оно закончилось в максимально короткий срок? Множество таких проблем систематически возникает перед экономистами, конструкторами, учеными.
Наконец, прогнозирование последствий тех или иных воздействий на объект может быть как относительно простым делом (в несложных физических системах), так и чрезвычайно сложным - на грани выполнимости - в системах биолого-экономических, социальных. Если относительно легко ответить на вопрос об изменении режима распространения тепла в тонком стержне в зависимости от изменений в составляющем его сплаве, то несравненно труднее проследить (предсказать) экологические и климатические последствия строительства крупной ГЭС или социальные последствия изменений налогового законодательства. Возможно, и здесь методы математического моделирования будут оказывать в будущем более значительную помощь.
Составим список величин, от которых зависит поведение объекта или ход процесса, а также тех величин, которые желательно получить в результате моделирования. Обозначим первые из них (входные) через х1,х2,..., хn„; вторые (выходные) через у1, у2,..., уn. Символически поведение объекта или процесса можно представить в виде
уj = Fj (х1, х2,…, хn) (j = 1,2…k),
где Fj — те действия, которые следует произвести над входными параметрами, чтобы получить результаты. Хотя запись F(х1, х2,…, хn) напоминает обозначение функции, мы здесь используем ее в более широком смысле. Лишь в простейших ситуациях здесь F есть функция в обычном смысле; чаще всего она выражает лишь наличие некоторой связи между входными и выходными параметрами модели.
Входные параметры хj могут быть известны «точно», т.е. поддаваться (по крайней мере, в принципе) измерению однозначно и с любой степенью точности — тогда они являются детерминированными величинами. Так, в классической механике, сколь сложной ни была бы моделируемая система, входные параметры детерминированы и, соответственно, детерминирован процесс эволюции такой системы. Однако в природе и обществе гораздо чаще встречаются процессы иного рода, когда значения входных параметров известны лишь с определенной степенью вероятности, т.е. эти параметры являются вероятностными {стохастическими), и, соответственно, случайным является процесс эволюции системы.
Для стохастической модели выходные параметры могут быть как величинами вероятностными, так и однозначно определяемыми. Например, на перекрестке улиц можно ожидать зеленого сигнала светофора и полминуты, и две минуты (с разной вероятностью), но среднее время ожидания есть величина вполне определенная, и именно она может быть объектом моделирования.
Важнейшим этапом моделирования является разделение входных параметров по степени важности влияния их изменений на выходные. Такой процесс называется ранжированием (разделением по рангам). Чаще всего невозможно, да и не нужно учитывать все факторы, которые могут повлиять на значения интересующих нас величин уj. От того, насколько умело выделены важнейшие факторы, зависит успех моделирования, быстрота и эффективность достижения цели. Выделить наиболее значимые факторы и отсеять менее важные может лишь специалист в той предметной области, к которой относится модель. Так, опытный учитель знает, что на успех контрольной работы влияет степень знания предмета и психологический настрой класса; однако, влияют и другие факторы — например, каким уроком по счету идет контрольная, какова в этот момент погода и т.д. — фактически проведено ранжирование.
Отбрасывание менее значимых факторов огрубляет объект моделирования и способствует пониманию его главных свойств и закономерностей. Умело ранжированная модель должна быть адекватна исходному объекту или процессу в отношении целей моделирования. Обычно определить, адекватна ли модель можно только в процессе экспериментов с ней, анализа результатов первоначального моделирования.
На рис. 8 проиллюстрированы две крайние ситуации: а) некоторый параметр хj, очень сильно влияет на результирующую величину уj; б) почти не влияет на неё. Ясно, что если все представляющие интерес величины уj реагируют на хj так, как изображено на рис. 9б, то хj является параметром, который при первом подходе может быть из модели исключен. Если же хотя бы одна из величин уj реагирует на изменение хj так, как изображено на рис. 9а, то хj нельзя исключать из числа значимых параметров.
Следующий этап - поиск математического описания. На этом этапе необходимо перейти от абстрактной формулировки модели к формулировке, имеющей конкретное математическое наполнение. В этот момент модель предстает перед нами в виде уравнения, системы уравнений, системы неравенств, дифференциального уравнения или системы таких уравнений и т.д.
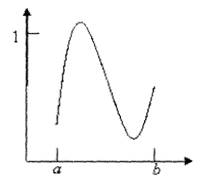
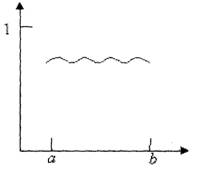
Рис. 8. Варианты степени влияния величины хj на результирующую величину уj
Когда математическая модель сформулирована, нужно выбрать метод ее исследования. Как правило, для решения одной и той же задачи есть несколько конкретных методов, различающихся эффективностью, устойчивостью и т.д. Oт верного выбора метода часто зависит успех всего процесса.
После разработки алгоритма и составления программы для ЭВМ необходимо решить с ее помощью простейшую текстовую задачу (желательно с заранее известным ответом) с целью устранения грубых ошибок. Это лишь начало процедуры тестирования, которую трудно описать формально исчерпывающим образом. По существу, тестирование может продолжаться долго и закончиться тогда, когда пользователь по своим профессиональным признакам сочтет программу верной.
3aтем следует собственно численный эксперимент, и выясняется, соответствует ли модель реальному объекту (процессу). Модель адекватна реальному процессу, если некоторые характеристики процесса, полученные на ЭВМ, совпадают с экспериментальными с заданной степенью точности. В случае несоответствия модели реальному процессу возвращаются к одному из предыдущих этапов.
§ 1.3 Различные классификации математических моделей
К классификации математических моделей можно подходить с разных позиций, положив в основу классификации различные принципы. Можно классифицировать модели но отраслям наук (математические модели по физике, биологии, социологии и т.д.) и по применяемому математическому аппарату (модели, основанные на использовании обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, стохастических методов, дискретных алгебраических преобразований и т.д.). Далее, если поинтересоваться общими закономерностями моделирования в разных науках (безотносительно к математическому аппарату) и поставить на первое место цели моделирования, то можно прийти к следующей классификации:
• дескриптивные (описательные) модели;
• оптимизационные модели;
• многокритериальные модели;
• игровые модели;
• имитационные модели.
Остановимся на этой классификации подробнее и поясним ее на примерах.
Моделируя движение кометы, вторгшейся в Солнечную систему, мы описываем ситуацию (предсказываем траекторию полета кометы, расстояние, на котором она пройдет от Земли и т.д.), т.е. ставим чисто описательные цели. У нас нет никаких возможностей повлиять на движение кометы, что-то изменить в процессе моделирования.
И оптимизационных моделях мы можем воздействовать на процессы, пытаясь добиться какой-то цели. В этом случае в модель входит один или несколько параметров, доступных нашему влиянию. Например, меняя тепловой режим в зернохранилище, мы можем стремиться подобрать такой, чтобы достичь максимальной сохранности зерна, т. е. оптимизируем процесс.
Часто приходится оптимизировать процесс по нескольким параметрам сразу, причем цели могут быть весьма противоречивыми. Например, зная цены на продукты и потребность человека в пище, организовать питание больших групп людей (в армии, летнем лагере и др.) как можно полезнее и как можно дешевле. Ясно, что эти цели, вообще говоря, совсем не совпадают, т.е. при моделировании будет несколько критериев, между которыми надо искать баланс. В этом случае говорят о многокритериальных моделях.
Игровые модели могут иметь отношение не только к детским играм (в том числе и компьютерным), но и к вещам весьма серьезным. Например, полководец перед сражением в условиях наличия неполной информации о противостоящей армии должен разработать план, в каком порядке вводить в бой те или иные части и т.п., учитывая возможную реакцию противника. В современной математике есть специальный раздел - теория игр, изучающий методы принятия решений в условиях неполной информации.
Наконец, бывает, что модель в большой мере подражает реальному процессу, т.е. имитирует его. Например, моделируя динамику численности микроорганизмов в колонии, можно рассматривать совокупность отдельных объектов и следить за судьбой каждого из них, ставя определенные условия для его выживания, размножения и т.д. При этом иногда явное математическое описание процесса не используется, заменяясь некоторыми словесными условиями (например, по истечении некоторого отрезка времени микроорганизм делится на две части, а другого отрезка - погибает). Другой пример - моделирование движения молекул в газе, когда каждая молекула представляется в виде шарика, и задаются условия поведения этих шариков при столкновении друг с другом и со стенками (например, абсолютно упругий удар); при этом не нужно использовать никаких уравнений движения.
Можно сказать, что чаще всего имитационное моделирование применяется в попытке описать свойства большой системы при условии, что поведение составляющих ее объектов очень просто и четко сформулировано. Математическое описание тогда производится на уровне статистической обработки результатов моделирования при нахождении макроскопических характеристик системы. Такой компьютерный эксперимент фактически претендует на воспроизведение натурного эксперимента. На вопрос же «зачем это делать?» можно дать следующий ответ: имитационное моделирование позволяет выделить «в чистом виде» следствия гипотез, заложенных в наши представления о микрособытиях, очистив их от неизбежного в натурном эксперименте влияния других факторов, о которых мы можем даже не подозревать. Если же такое моделирование включает и элементы математического описания событий на микроуровне, и если исследователь при этом не ставит задачу поиска стратегии регулирования результатов (например, управления численностью колонии микроорганизмов), то отличие имитационной модели от дескриптивной достаточно условно; это, скорее, вопрос терминологии.
Еще один подход к классификации математических моделей подразделяет их на детерминированные и стохастические (вероятностные). В детерминированных моделях входные параметры поддаются измерению однозначно и с любой степенью точности, т.е. являются детерминированными величинами. Соответственно, процесс эволюции такой системы детерминирован. В стохастических моделях значения входных параметров известны лишь с определенной степенью вероятности, т.е. эти параметры являются стохастическими; соответственно, случайным будет и процесс эволюции системы. При этом, выходные параметры стохастической модели могут быть как величинами вероятностными, так и однозначно определяемыми.
Наконец, если ограничиться непрерывными детерминистскими моделями, то их часто подразделяют на системы с сосредоточенными параметрами и системы с распределенными параметрами. Системы с сосредоточенными параметрами описываются с помощью конечного числа обыкновенных дифференциальных уравнений для зависящих от времени переменных. Пространство состояний имеет здесь конечную размерность (число степеней свободы системы конечно). В противоположность этому под системами с распределенными параметрами понимают системы, описываемые конечным числом дифференциальных уравнений в частных производных. Здесь переменные состояния в каждый момент времени есть функции одной или нескольких пространственных переменных. Пространство состояний имеет в этом случае бесконечную размерность, т.е. система обладает бесконечным числом степеней свободы.
Глава 2. Методические аспекты обучения информационному моделированию учащихся старших классов в рамках элективного курса информатики
§ 2.1 Психолого-педагогическая характеристика учащихся старших классов
Переход от детства к взрослости составляет основное содержание и специфическое отличие всех сторон развития подростка в этот период: физического, умственного, нравственного, социального. Важность подросткового возраста определяется и тем, что в нем закладываются основы и намечаются общие направления формирования моральных и социальных установок личности[3].
Психологические особенности подросткового возраста получили название «подросткового комплекса» [8], который включает в себя:
- чувствительность к оценке посторонних своей внешности в сочетании с крайней самонадеянностью и безаппеляционными суждениями в отношении окружающих;
- внимательность, которая порой уживается с поразительной черствостью;
- болезненную застенчивость в сочетании с развязностью, желанием быть признанным и оцененным другими, - с показной независимостью;
- борьбу с авторитетами, общепринятыми правилами и распространенными идеалами - с обожествлением случайных кумиров, а чувственное фантазирование с сухим мудрствованием.
Характерной чертой этого возраста является пытливость ума, стремление к познанию, подросток жадно стремиться овладеть как можно большим количеством знаний, при этом не обращая должного внимания на их систематичность. Подростки направляют умственную деятельность на ту сферу, которая больше всего их увлекает. Этот возраст характеризуется эмоциональной неустойчивостью и резкими колебаниями настроения (от экзальтации до депрессии). Наиболее аффективные бурные реакции возникают при попытке ущемить самолюбие.
Важным этапом социально-физиологического созревания старшеклассников является процесс формирования самосознания. В его основе лежит способность человека отличать себя от своей жизнедеятельности, осознанное отношение к своим потребностям и способностям, влечениям, переживаниям и мыслям [3].
Подросток стремится к самостоятельности, но в проблемных жизненных ситуациях он старается не брать на себя ответственность за принимаемые решения, и ждет помощи со стороны взрослых [8].
Ведущей деятельностью в этом возрасте является коммуникативность. Суть «подросткового комплекса» составляют свои, свойственные этому возрасту и определенным психологическим особенностям поведенческие модели, специфические подростковые поведенческие реакции на воздействия окружающей среды [12].
Психологически переходный возраст очень противоречив, для него характерны диспропорции уровней и темпов развития. Подростковое «чувство взрослости» главным образом новый уровень притязаний, предвосхищяющий положение, которого подросток фактически не достиг. Для подростка очень важно, чтобы его взрослость была замечена окружающими, чтобы форма его поведения не была детской. Ценность работы для подростка определяется ее взрослостью, а возникающие представления о нормах поведения провоцируют на обсуждение поведения взрослых, обычно весьма не лицеприятно, отсюда и типичные возрастные конфликты [3].
Параллельно физиологическим и социальным изменениям происходит также изменение познавательных (когнитивных) способностей подростков. Когнитивные изменения в отрочестве—юности характеризуются развитием мышления на уровне формальных операций. Этот тип мышления необходим для абстрактного мышления, не привязанного к существующим в данный момент конкретным условиям внешней среды. Вследствие роста метапознавательных умений, таких как текущий самоконтроль и саморегуляция, подростки могут размышлять о своих собственных мыслительных процессах и о мышлении других людей. Сторонники информационного подхода к развитию также утверждают, что подростки приобретают метапознавательные умения, которые, в свою очередь, влияют на эффективность их познавательных стратегий и развитие коммуникативных способностей [8].
Мышление на уровне формальных операций требует способности формулировать, проверять и оценивать гипотезы. Оно предполагает манипулирование не только известными элементами, которые можно проверить, но также вещами, противоречащими фактам (Например: «Давайте предположим, просто ради обсуждения, что...») [3].
Существенными свойствами подросткового мышления являются следующие черты [12]:
1) способность учитывать все комбинации переменных при поиске решения проблемы;
2) способность предполагать, какое влияние одна переменная окажет на другую.
3) способность объединять и разделять переменные гипотетико-дедуктивным образом (Если есть X, то произойдет Y).
Этот возраст также представляет собой особый интерес в связи с тем, что для большинства подростков еще не наступил момент самоопределения; не встала еще остро проблема дальнейшего выбора - либо получать среднее образование в школе и ориентироваться в далеком будущем на высшее учебное заведение, либо совмещать образование с получением профессии в средних специальных учреждениях, таких как колледжи, техникумы и пр.
Подросток выступает в качестве субъекта учебной деятельности, которая прежде всего определяется через два типа мотивов: мотивация достижения и познавательная мотивация. Последняя является основой учебно-познавательной деятельности. Она возникает в проблемной ситуации и развивается при правильном взаимодействии отношении учащихся и преподавателей.
§ 2.2 Информационные технологии в обучении
Процессы информатизации современного общества и тесно связанные с ними процессы информатизации всех форм образовательной деятельности характеризуются процессами совершенствования и массового распространения современных информационных и коммуникационных технологий (ИКТ). Подобные технологии активно применяются для передачи информации и обеспечения взаимодействия преподавателя и обучаемого в современных системах открытого и дистанционного образования. Современный преподаватель должен не только обладать знаниями в области ИКТ, но и быть специалистом по их применению в своей профессиональной деятельности.
Слово "технология" имеет греческие корни и в переводе означает науку, совокупность методов и приемов обработки или переработки сырья, материалов, полуфабрикатов, изделий и преобразования их в предметы потребления. Современное понимание этого слова включает и применение научных и инженерных знаний для решения практических задач. В таком случае информационными и телекоммуникационными технологиями можно считать такие технологии, которые направлены на обработку и преобразование информации.
Информационные и коммуникационные технологии (ИКТ) – это обобщающее понятие, описывающее различные устройства, механизмы, способы, алгоритмы обработки информации [11].
Важнейшим современным устройствами ИКТ являются компьютер, снабженный соответствующим программным обеспечением и средства телекоммуникаций вместе с размещенной на них информацией.
Основным средством ИКТ для информационной среды любой системы образования является персональный компьютер, возможности которого определяются установленным на нем программным обеспечением. Основными категориями программных средств являются системные программы, прикладные программы и инструментальные средства для разработки программного обеспечения. К системным программам, в первую очередь, относятся операционные системы, обеспечивающие взаимодействие всех других программ с оборудованием и взаимодействие пользователя персонального компьютера с программами [11]. В эту категорию также включают служебные или сервисные программы.
К прикладным программам относят программное обеспечение, которое является инструментарием информационных технологий – технологий работы с текстами, графикой, табличными данными и т.д. [11]
В современных системах образования широкое распространение получили универсальные офисные прикладные программы и средства ИКТ: текстовые процессоры, электронные таблицы, программы подготовки презентаций, системы управления базами данных, органайзеры, графические пакеты и т.п.
С появлением компьютерных сетей и других, аналогичных им средств ИКТ образование приобрело новое качество, связанное в первую очередь с возможностью оперативно получать информацию из любой точки земного шара. Через глобальную компьютерную сеть Инернет возможен мгновенный доступ к мировым информационным ресурсам (электронным библиотекам, базам данных, хранилищам файлов, и т.д.). В самом популярном ресурсе Интернет – всемирной паутине WWW опубликовано порядка двух миллиардов мультимедийных документов.
В сети доступны и другие распространенные средства ИКТ, к числу которых относятся электронная почта, списки рассылки, группы новостей, чат.
Разработаны специальные программы для общения в реальном режиме времени, позволяющие после установления связи передавать текст, вводимый с клавиатуры, а также звук, изображение и любые файлы. Эти программы позволяют организовать совместную работу удаленных пользователей с программой, запущенной на локальном компьютере.
С появлением новых алгоритмов сжатия данных доступное для передачи по компьютерной сети качество звука существенно повысилось и стало приближаться к качеству звука в обычных телефонных сетях. Как следствие, весьма активно стало развиваться относительно новое средство ИКТ – Интернет-телефония. С помощью специального оборудования и программного обеспечения через Интернет можно проводить аудио и видеоконференции.
Для обеспечения эффективного поиска информации в телекоммуникационных сетях существуют автоматизированные поисковые средства, цель которых – собирать данные об информационных ресурсах глобальной компьютерной сети и предоставлять пользователям услугу быстрого поиска. С помощью поисковых систем можно искать документы всемирной паутины, мультимедийные файлы и программное обеспечение, адресную информацию об организациях и людях.
Существует несколько основных классов информационных и телекоммуникационных технологий, значимых с точки зрения систем открытого и дистанционного образования. Одними из таких технологий являются видеозаписи и телевидение. Видеопленки и соответствующие средства ИКТ позволяют огромному числу студентов прослушивать лекции лучших преподавателей. Видеокассеты с лекциями могут быть использованы как в специальных видеоклассах, так и в домашних условиях. Примечательно, что в американских и европейских курсах обучения основной материал излагается в печатных издания и на видеокассетах.
Мощной технологией, позволяющей хранить и передавать основной объем изучаемого материала, являются образовательные электронные издания, как распространяемые в компьютерных сетях, так и записанные на CD-ROM. Индивидуальная работа с ними дает глубокое усвоение и понимание материала. Эти технологии позволяют, при соответствующей доработке, приспособить существующие курсы к индивидуальному пользованию, предоставляют возможности для самообучения и самопроверки полученных знаний. В отличие от традиционной книги, образовательные электронные издания позволяют подавать материал в динамичной графической форме.
-Совершенствование организации преподавания, повышение индивидуализации обучения;
- Повышение продуктивности самоподготовки учащихся;
- Индивидуализация работы самого учителя;
- Ускорение тиражирования и доступа к достижениям педагогической практики;
- Усиление мотивации к обучению;
- Активизация процесса обучения, возможность привлечения учащихся к исследовательской деятельности;
- Обеспечение гибкости процесса обучения.
§ 2.3 Анализ подходов к обучению информационному моделированию в школьном курсе информатики
Место, которое занимает тема информационного моделирование, в различных учебниках существенно различается. В целом, в процессе развития школьной информатики следует отметить увеличение веса данной линии в общем содержании курса.
В первом школьном учебнике информатики затрагивается только тема математического моделирования. Во введении отмечается:
«Важнейшим средством современного научного исследования является математическое моделирование физических явлений и исследование этих моделей с помощью ЭВМ». Далее говорится о вычислительном эксперименте. Термины «модель», «моделирование» употребляются как очевидные, без какого-либо пояснения.
В конце первой части учебника имеется материал на тему «Построение алгоритмов для решения задач из курса физики». Здесь рассматриваются три задачи:
1) расчет сопротивления проводника по результатам лабораторных измерений;
2) расчет движения пружинного маятника;
3) расчет распределения температуры в квадратной теплопроводной пластине.
Вводится понятие вычислительной модели, под которой подразумевается программная реализация численного метода решения задачи.
Первая задача иллюстрирует статический метод решения. В этом случае численной обработке подвергаются результаты большого числа измерений (силы тока в цепи при различных значениях напряжений), дается готовая расчетная формула, которая получена путем применения метода наименьших квадратов. По этой формуле составляется программа расчета. В этом примере подчеркивается мысль о том, что применение ЭВМ снимает проблему обработки больших объемов данных, что дает возможность получать более точные результаты, чем при неавтоматизированных расчетах.
Следующие две задачи иллюстрируют другой прием, характерный для вычислительных моделей — прием дискретизации, (дискретизация — это разбиение области решения задачи на конечное число промежутков. В пределах каждого такого промежутка допускается некоторое упрощенное поведение исследуемого объекта). При расчете движения пружинного маятника время движения разбивается на конечные шаги Л!, в пределах каждого из которых движение считается равноускоренным. Такое предположение позволяет принимать знакомые школьникам формулы равноускоренного движения для расчета изменения координаты и скорости на каждом шаге.
В задаче теплопроводности используется пространственная дискретизация. Поверхность пластины разбивается на маленькие квадратные ячейки. Считается, что в пределах каждой такой ячейки температура остается постоянной. Однако на границах ячеек температура изменяется скачком. Распределение температуры на внешних границах поддерживается неизменным.
В таком случае все температурное поле представляется матрицей Т[М,], каждый элемент которой — температура в соответствующей ячейке. Из уравнения теплового баланса выводится формула для расчета температуры во внутренних ячейках:
T[I,j] =(T[I-1,j] + T[I,j-1] + T[I,j+1] + T[I+1,j])/4
Смысл ее очень простой: температура во всяко внутренней ячейке равна среднему арифметическому значению температур на ее границах. Подчеркнем, что ведется расчет установившегося (стационарного) распределения температур. Решение задачи производится итерационным методом: первоначально задается постоянное распределение температуры во всей пластине. И далее, отталкиваясь от заданных температур границы пластины, ведется итерационное уточнение температуры во внутренних ячейках. Процесс продолжается до установления распределения температуры с заданной точностью.
Для двух последних задач, использующих метод дискретизации, делается общий вывод: чем меньшими берутся промежутки дискретизации (меньше Л, большее число ячеек разбиения пластины); тем результаты расчетов более точные. Высокое быстродействие современных ЭВМ позволяет достигать высокой точности результатов, полученных на подобных вычислительных моделях, данные примеры обсуждения столь подробно в связи с их характерностью для иллюстрации методики математического моделирования в школьной информатике. Цель этой методики: не привлекая аппарата высшей математики, дать представление о возможностях вычислительных моделей, реализованных на ЭВМ.
В учебниках информатики второго поколения информационному моделирования уделяется большее внимание. В учебнике А. Г. Кушниренко [15] тема моделирования раскрывается в двух аспектах. В разделе «Моделирование и вычислительный эксперимент на ЭВМ» рассматривается тот же подход к математическому моделированию физических процессов, что и в учебнике А. П. Ершова: метод дискретизации. Обсуждается задача расчета свободного падения парашютиста с учетом сопротивления воздуха.
В главе 3 того же учебника имеется параграф «Кодирование информации величинами алгоритмического языка. Информационные модели». Здесь вводится следующее определение модели: «Набор величин, содержащий всю необходимую информацию об исследуемых объектах и процессах, в информатике называется информационной моделью. Как и любая модель, информационная модель содержит не всю информацию о моделируемых явлениях, а только ту ее часть, которая нужна для рассматриваемых задач», данное определение требует уточнения: очевидно, что модель — это не только набор величин, но и отношения, связи между ними.
В соответствии с данным выше определение, информационные модели представляются как наборы величин в алгоритмах: скалярных переменных различных типов, массивов (таблиц) различных размеров и размерностей. В частности некоторые геометрические объекты описываются наборами величин, определяющих их параметры в декартовых координатах.
В параграфе «Информационное моделирование исполнителей на ЭВМ» рассматриваются способы программирования на учебном алгоритмическом языке работы учебных исполнителей — Робот и Черепашка — введенных в разделе алгоритмизации. Иначе говоря, в качестве модели исполнителя выступает не только набор характеризующих его параметров, но и алгоритм его работы. Если в таком контексте использовать понятие модели, то здесь следовало бы говорить об алгоритмической модели.
В учебнике А. Г. Гейна [4] понятие модели является центральным. Это понятие как стержень связывает содержание всего курса в единое целое. В соответствии с авторской концепцией «основной целью курса является обучение школьников решению жизненных задач с помощью ЭВМ». Под задачей понимают некоторую проблему, требующую решения. Везде в учебнике термин «модель» употребляется в контексте «модель задачи» и в комплексе с понятием четко сформулированной задачи. «Четко сформулировать задачу — это значит высказать те предположения, которые позволяют в море информации об изучаемом явлении или объекте выудить исходные данные, определить, что будет служить результатом и какова связь между исходными данными и результатом. Все это: предположения, исходные данные, результаты и связи между ними — называют моделью задачи». Если же связь между исходными данными и результатами выражается через математические соотношения, то имеем математическую модель. Далее описываются этапы разработки математической модели. «Создавая математическую модель задачи, нужно:
1) выделить предположения, на которых будет основана математическая модель;
2) определить, что считать исходными данными и результатами;
3) записать математические соотношения (формулы, уравнения, неравенства и т.д.), связывающие результаты с исходными данными».
Для решения поставленной задачи путем использования построенной математической модели применяется компьютер. А для того чтобы можно было использовать компьютер, требуется построить алгоритм и написать программу. Выполнение программы на ЭВМ приведет к искомому решению. Использование полученной программы и анализ результатов называется вычислительным экспериментом. В учебнике подчеркивается тот факт, что критерием правильности полученной модели является степень соответствия между расчетными результатами и реальными, получаемыми на практике. Если такого соответствия с допустимой точностью не получается, то модель требует уточнения.
Описанная методическая схема применяется на протяжении всего учебника к целому ряду задач. Причем задачи весьма разнообразные по своей методической сути. Так, задача о выборе места строительства железнодорожной станции на языке высшей математики называется вариационной задачей. Она сводится к минимизации функционала, выбранного в качестве критерия оптимальности места расположения станции. Безусловно, в учебнике не употребляются непонятные для десятиклассников слова «вариационная задача», «функционал». Постановка задачи осуществляется на смысловом уровне, а методом ее решения является дискретизация с подключением алгоритма выбора минимального значения в числовом массива.
Другая задача — планирование производства некоторого набора изделий на предприятии. Эта задача из области линейного программирования. Она сводится к решению системы неравенств при условии поиска экстремума целевой функции (максимального значения прибыли предприятия). Известно, что для решения такой задачи в линейном программировании применяется симплекс-метод. В учебнике, как и для предыдущей задачи, используется модельный численно-алгоритмический подход для простейшего случая — всего двух типов изделий: изделия А и изделия В. Поскольку количество изделий — величины х и у — принимают только целочисленные значения в ограниченных диапазонах, то задача, по сути своей, является дискретной, т.е. искусственной дискретизации не требуется. Решение сводится к вычислению матрицы значений прибыли — У(х,у) для всех вариантов величин х и у — и поиску в этой матрице наибольшего значения. Такой метод можно еще назвать переборным: производится полный перебор всех возможных значений х и у.
Если число изделий больше двух: 3, 4, 5 и т.д. — полный перебор становится нерациональным и может оказаться слишком долгим даже для компьютера. В этом случае никуда не уйти от симплекс-метода. В учебном программном обеспечении курса имеется прикладная программа «Оптима», предназначенная для решения задачи планирования (линейного программирования) симплекс-методом, допустимое число параметров — до шести. В учебнике не раскрывается суть метода, однако его название произносится. В лабораторной работе ученикам предлагается воспользоваться данной прикладной программой. Такая ситуация достаточно жизненна, поскольку довольно часто пользователи успешно применяют для решений своих задач готовые прикладные программы и при этом не всегда обязаны знать заложенные в них методы. Главное что требуется от пользователя — уметь грамотно поставить задачу, владеть интерфейсом с Прикладной программой.
Перечислены не все задачи, рассмотренные в учебнике Гейна, однако даже этот перечень дает представление о широте подхода авторов к теме моделирование в школьной информатике, данный учебник предназначен для старших классов (10-11) и ориентируется на уровень физико-математической подготовки учащихся этого возраста. Судя даже по описанным выше задачам, требования к этому уровню довольно высокие, данный курс может быть хорошей основой для формирования учебного комплекса физика-математика. Такое направление является наиболее подходящим для школ физико-математического профиля.
С содержательной и методической точки зрения линия математического моделирования в учебнике проработана достаточно основательно. Однако другие направления информационного моделирования остаются за рамками учебника.
В качестве основного средства реализации математических моделей на ЭВМ выступает программирование. Лишь применительно к решению одной задачи используются электронные таблицы. Это обстоятельство объясняется тем, что второй ведущей темой курса, после моделирования, является алгоритмизация. На примерах решения «жизненных задач» авторы учат не только построению математических моделей, но и составлению алгоритмов решения на основе этих моделей. Такая целевая установка с общей тенденцией, характерной для первых двух этапов эволюции информатики.
Современной тенденцией в развитии школьной информатики является увеличение веса содержательной линии информационных технологий. С этой позиции в качестве инструментального средства математического моделирования больше используют электронные таблицы. Для многих задач подходящим средством могут оказаться специализированные математические пакеты (Математика и др.), но они, как правило, менее доступны для школы, чем табличные процессоры. Кроме того, в базовом курсе информатики желательно обходиться прикладным ПО общего назначения. Электронные таблицы являются достаточно мощным математического моделирования. Практически все задачи, рассматриваемые в учебнике, можно решать с помощью электронных таблиц. Методика использования электронных таблиц в школьной информатике требует своего развития.
В учебнике того же авторского коллектива тема моделирования не ограничивается только математическим моделированием. Дается общее представление о моделировании. Определение понятия «модель» отсутствует, но приводится следующее определение: «Замена реального объекта (процесса или явления) его копией, отражающей существенные свойства этого объекта (процесса или явления), называется моделированием». Отсюда надо сделать вывод, что модель — это и есть та самая копия, что совершенно справедливо. Далее говорится о разделении моделей на материальные (натурные) и информационные, о различных формах информационных моделей (словесное описание, схема и др.), об ограниченности и целенаправленности информационных моделей. Тема математического моделирования также находит свое отражение в учебнике. Здесь авторы повторяют концепции, используемые в учебнике. Понятие «модель задачи» связывается с понятием «хорошо поставленная задача». Подчеркивается связь между моделью задачи и исполнителем, который будет применен для ее реализации. «Модель задачи, составленную в расчете на исполнителя, имитированного на ЭВМ, будем называть компьютерной моделью. Это означает, что исходные данные, результаты и связи между исходными данными и результатами представлены в виде, «понятном» компьютерному исполнителю». Далее дается вывод о том, что если данные и результаты представляют собой числовые величины, а исполнитель умеет только вычислять, то мы имеем дело с математической моделью. Утверждается, что решение всякой задачи с помощью ЭВМ происходит в четыре этапа.
Здесь смысл возвратной стрелки — в возможности изменения или уточнения модели, в случае если результаты расчетов окажутся неудовлетворительными.
В качестве примера компьютерной математической модели приводится задача о выборе места для железнодорожной станции, из учебника. Для реализации модели здесь снова применяется язык программирования.
Современная концепция базового курса информатики ориентирует на широкий подход к теме моделирования. Безусловно, математическое моделирование является важным разделом этой линии, но отнюдь не единственным. Многие разделы базового курса имеют прямое отношение к моделированию, в том числе и темы, относящиеся к технологической линии. Текстовые и графические редакторы, программное обеспечение телекоммуникаций можно отнести к средствам, предназначенным для рутинной работы с информацией: позволяющим набрать текст, построить чертеж, передать или принять информацию по сети. В то же время такие программные средства информационных технологий, как СУБД, табличные процессоры, следует рассматривать как инструменты для работы с информационными моделями. Алгоритмизация и программирование также имеют прямое отношение к моделированию. Следовательно, линия моделирования является сквозной для целого ряда разделов базового курса.
Информатика в настоящее время является одной из фундаментальных отраслей научного знания, формирующей системно-информационный подход к анализу окружающего мира, изучающей информационные процессы, методы и средства получения, преобразования, передачи, хранения и использования информации; стремительно развивающейся областью практической деятельности человека, связанной с использованием информационных технологий [14]. Важнейший методологический принцип информатики – изучение объектов и явлений окружающего мира с точки зрения процессов сбора, обработки и выдачи информации о них, а также определённого сходства этих процессов при реализации в искусственных и естественных (в том числе биологических и социальных) системах.
§ 2.4 Формы и методы обучения информационному моделированию
Основными формами обучения компьютерному моделированию являются лекционные, лабораторные и зачетные занятия. Обычно работа по созданию и подготовке к изучению каждой новой модели занимает 3—4 урока. В ходе изложения материала ставятся задачи, которые в дальнейшем должны быть решены учащимися самостоятельно, в общих чертах намечаются пути их решения. Формулируются вопросы, ответы на которые должны быть получены при выполнении заданий. Указывается дополнительная литература, где могут быть найдены вспомогательные сведения для более успешного выполнения заданий.
Формой организации занятий при изучении нового материала рекомендуется лекция, охватывающая, как правило, весь урок. Применение лекционного метода целесообразно в следующих случаях:
• при прохождении нового материала, мало или совсем не связанного с предыдущим;
• при сообщении учащимся сведений о практическом применении изученных закономерностей;
• при выводе сложных закономерностей с применением большого математического аппарата и ряда логических умозаключений;
• при проведении уроков проблемного характера.
Как следует заметить, перечисленные условия применениям лекционного метода совпадают с условиями изучения профильных курсов, ориентированных на компьютерное моделирование, при исследовании очередной содержательной задачи и введении новой модели, что доказывает целесообразность его применения при изложении нового материала. Экспериментальное преподавание различных вариантов курса также подтверждает это.
После завершения обсуждения очередной информационной модели учащиеся имеют в своем распоряжении необходимые теоретические сведения и набор заданий для дальнейшей ведется над одной из них по выбору учащихся или учителя, если одна — все работают над ней, различаться могут лишь конкретные задания (уровень сложности которых может зависеть от подготовленности соответствующего учащегося). В ходе подготовки к выполнению задания учащиеся выбирают подходящий метод решения, с помощью какого-либо известного частного решения тестируют разработанную программу. В случае вполне возможней затруднений при выполнении заданий дается консультация, делается предложение более детально проработать указанные разделы в литературных источниках.
Как отмечают практически все разработчики профильных курсов, ориентированных на моделирование, наиболее адекватным практической части обучения компьютерному моделированию является метод проектов. Задание формулируется для ученика в виде учебного проекта и выполняется в течение нескольких уроков, причем основной организационной формой являются компьютерные лабораторные работы. Экспериментальная апробация курсов моделирования подтвердила целесообразность применения такой формы организации занятий.
Обучение моделированию с помощью метода учебных проектов может быть реализовано на разных уровнях. Первый — проблемное изложение процесса выполнения проекта, которое ведет учитель. Второй — выполнение проекта учащимися под руководством учителя. Третий — самостоятельное выполнение учащимися учебного исследовательского проекта.
Результаты работы должны быть представлены в численном виде, в виде графиков, диаграмм. Если имеется возможность, процесс представляется на экране компьютера в динамике. По окончании расчетов и получении результатов проводится их анализ, сравнение с известными фактами из теории, подтверждается достоверность и проводится содержательная интерпретация, что в дальнейшем отражается в письменном отчете.
Если результаты удовлетворяют ученика и учителя, то работа считается завершенной, и ее конечным этапом является составление отчета. Отчет включает в себя краткие теоретические сведения по изучаемой теме, математическую постановку задачи, алгоритм решения и его обоснование, программу для компьютера, результаты работы программы, анализ результатов и выводы, список использованной дополнительной литературы.
Когда все отчеты составлены, на зачетном занятии учащиеся выступают с краткими сообщениями о проделанной работе, защищают свой проект. Это является эффективной формой отчета группы, выполняющей проект, перед классом, включая постановку задачи, построение формальной модели, выбор методов работы с моделью, реализацию модели на работу с итоговой моделью, интерпретацию полученных реализацию модели на работу с итоговой моделью, интерпретацию полученных результатов, прогнозирование, действенность этой установки подтверждена на опыте. В итоге учащиеся получают две оценки: первую за проработанность проекта и успешность его защиты, вторую — за программу, оптимальность ее алгоритма, интерфейс и т.д. Также учащиеся получают в ходе опросов по теории.
В концепции профильного обучения на старшей ступени общего образования обозначены цели перехода к профильному обучению, среди которых выделяется цель создания условий для существенной дифференциации содержания обучения старшеклассников с широкими и гибкими возможностями построения школьниками индивидуальных образовательных программ. С этой целью помимо профильных общеобразовательных предметов вводятся элективные курсы, обязательные для посещения по выбору учащихся, дополняющие содержание профиля, что позволяет удовлетворять разнообразные познавательные интересы школьников [14].
§ 2.5 Элективные курсы в профильном обучении
Элективные курсы реализуются за счёт школьного компонента базисного учебного плана и выполняют следующие основные функции:
1) «надстройки» профильного курса, когда такой дополненный профильный
курс становится в полной мере углублённым (а школа (класс), в котором он изучается, превращается в традиционную школу с углублённым изучением отдельных предметов);
2) развивают содержание одного из базисных курсов, изучение которого осуществляется на минимальном общеобразовательном уровне, что позволяет поддерживать изучение смежных учебных предметов на профильном уровне или получить дополнительную подготовку для сдачи единого государственного экзамена по выбранному предмету на профильном уровне;
3) способствует удовлетворению познавательных интересов в различных областях деятельности человека.
Можно выделить следующие типы элективных курсов информатики (рис. 11).
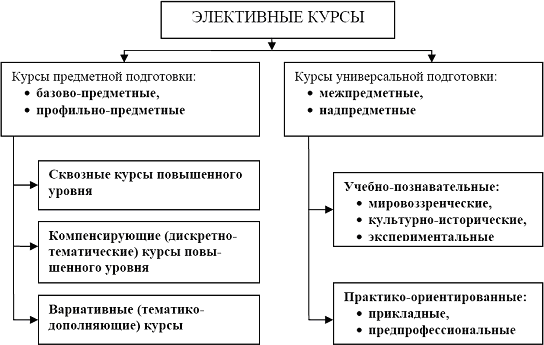
Рис.11 Классификация элективных курсов.
I. Курсы предметной подготовки – элективные курсы, задача которых – углубление и расширение знаний по предметам, входящим в базовый (базово-предметные курсы) или профильный (профильно-предметные курсы) компонент учебного плана профиля. В свою очередь, элективные курсы предметной подготовки (как базово-предметные, так и профильно-предметные) можно разделить на три группы по признаку тематического согласования учебного предмета и элективного курса.
1) Сквозные курсы повышенного уровня, направленные на углубление того или иного учебного предмета, имеющие как тематическое, так и временное согласование с этим учебным предметом. Выбор такого элективного курса позволит изучить выбранный предмет на углублённом уровне, в этом случае все разделы курса углубляются более или менее равномерно.
2) Компенсирующие (дискретно-тематические) курсы повышенного уровня – элективные курсы, в которых углублённо изучаются отдельные разделы предмета, входящего в базовый или профильный компонент.
3) Вариативные (тематико-дополняющие) курсы – элективные курсы, в которых углублённо изучаются отдельные разделы учебного предмета, не входящие в обязательную программу данного предмета.
II. Курсы универсальной подготовки – элективные курсы, удовлетворяющие познавательные интересы учащихся в областях деятельности человека, выходящих за рамки выбранного им профиля. По признаку формирования содержательного компонента универсальные курсы можно подразделить на межпредметные и надпредметные элективные курсы. Межпредметные элективные курсы интегрируют содержание учебных предметов, входящих в учебный план профиля. Надпредметные элективные курсы ориентированы на изучение предметов, не входящих в учебный план.
В свою очередь, элективные курсы универсальной подготовки (как межпредметные, так и надпредметные) по признаку «ведущей деятельности» можно разделить на две группы: учебно-познавательные и практико-ориентированные.
В составе учебно-познавательных курсов выделим [14]:
- мировоззренческие элективные курсы, посвящённые изучению методов познания природы;
- культурно-исторические элективные курсы, посвящённые истории предмета как входящего в учебный план школы, так и не входящего в него;
- экспериментальные элективные курсы, посвящённые изучению методов решения задач, составлению и решению задач на основе эксперимента.
Практико-ориентированные элективные курсы можно подразделить на:
- прикладные курсы – элективные курсы, цель которых – знакомство учащихся с важнейшими путями и методами применения знаний на практике, развитие интереса учащихся к современной технике и производству;
- предпрофессиональные курсы – элективные курсы, реализующие программы предпрофессильной подготовки и ориентированные на приобретение школьниками образовательных результатов для успешного продвижения на рынке труда.
Элективные курсы, хотя и различаются по целям и содержанию, должны соответствовать запросам учащихся, которые их выбирают. Элективные курсы как бы «компенсируют» во многом достаточно ограниченные возможности базовых и профильных курсов в удовлетворении разнообразных образовательных потребностей старшеклассников.
Профильное обучение – это не только дифференциация образования, а как правило по-другому построенный процесс. В этой связи в примерных учебных планах отдельных профилей в рамках времени, отводимого на элективные курсы, предусмотрены часы на организацию учебных практик, проектов, исследовательской деятельности. Данные формы обучения, наряду с развитием самостоятельной учебной деятельности учащихся, применение новых методов обучения (в частности, дистанционного обучения, деловых игр и др.), станут важным фактором успешного проведения занятий по элективным курсам [14].
В настоящее время разрабатываются учебные пособия по элективным курсам информатики, появляется возможность на примере учебных пособий по элективным курсам отработать условия реализации мотивационной функции учебника. Это может привести к новым подходам структурирования содержания учебных предметов. Традиционный подход основывается на логике базовой науки. Другой подход может заключаться в отборе проблем, явлений, процессов, ситуаций, изучение которых соответствовало бы познавательным запросам учащихся. Такой подход может способствовать формированию учащихся как субъектов образовательной деятельности. С другой стороны, нельзя забывать о главной задаче российской образовательной политики – обеспечения современного качества образования на основе сохранения его фундаментальности и соответствия актуальным и перспективным потребностям личности, общества и государства. Таким образом, современная школа не должна отказываться от знаний, умений и навыков, но считать приоритетным направлением деятельности способствование развитию школьника, научить его решать учебные и жизненные проблемы, научить учиться.
Специфика содержания элективных курсов по информатике определяется рядом факторов, в качестве важнейших выделим следующие:
- интенсивный характер межпредметных связей информатики с другими учебными предметами, широкое использование понятийного аппарата, методов и средств, присущих этой отрасли научного знания при изучении практически всех предметов;
- значение изучения информатики для формирования ключевых компетенций выпускника современной школы, приобретения образовательных достижений, востребованных на рынке труда;
- исключительная роль изучения информатики в формировании современной научной картины мира, которая может сравниться по значимости в школьном образовании только с изучением физики;
- интегрирующая роль информатики в содержании общего образования человека, позволяющая связать понятийный аппарат естественных, гуманитарных и филологических учебных дисциплин.
По заданию Министерства образования Национальный фонд подготовки кадров провел конкурс учебно-методических пособий по элективным курсам. В результате конкурса подготовлены программы, учебные и методические материалы по элективным курсам по каждому учебному предмету.
Элективный курс «Исследование информационных моделей с использованием систем объектно-ориентированного программирования и электронных таблиц» (автор Н.Д. Угринович) может быть востребован в ряде профилей на старшей ступени школы, выделим две основные причины: в ходе изучения данного курса учащиеся строят и исследуют математические, физические, химические, биологические и экономические модели; моделирование, особенно компьютерное, стало одним из основных общенаучных методов исследования, методов познания мира.
Метод проектов составляет основу методики обучения данному курсу, значительная часть этих проектов – практические задания для самостоятельного выполнения, уровень их реализации является главным показателем и средством оценки достижений старшеклассников. Содержание этого курса характеризуется вариативностью, поскольку оно ориентировано на различные по уровню способности и познавательные интересы учащихся. В учебном процессе предлагается разрабатывать компьютерные модели с использованием систем объектно-ориентированного программирования Visual Basic и Delphi, а также электронных таблиц Microsoft Excel и StarOffice Calc.
Элективный курс «Компьютерная графика» (автор Л.А. Залогова) предназначен для учащихся, обучающихся в естественно-математическом профиле, однако может быть интересен в социально-гуманитарном профиле. В этом курсе рассматриваются: основные вопросы создания, редактирования и хранения изображений; особенности работы с изображениями в растровых программах; методы создания иллюстраций в векторных программах. Для создания собственных иллюстраций используется векторная программа CorelDRAW, а для редактирования изображений и монтажа фотографий – программа Adobe PhotoShop.
В элективном курсе «Технология создания сайтов» (авторов А.В. Хуторской, А.П. Орешко) в явном виде просматривается ориентация на деятельностный подход и личностно-ориентированную парадигму в обучении; реализуется направленность на комплексный характер учебных достижений школьников. В процессе освоения курса каждый учащийся создаёт личностно значимую для него образовательную продукцию – сначала простейшие веб-страницы, затем их отдельные элементы и целостные веб-сайты. Основной тип занятий – практикум. Изучение нового материала носит сопровождающий характер. Ученики изучают его с целью создания запланированного продукта – графического файла, эскиза веб-страницы, элемента сайта и т. п. В рамках данного курса учащиеся учатся программировать на языках HTML, Dynamic HTML, CSS; овладевают способами работы с программой Flash; передают информацию в сеть Интернет с помощью протокола FTP, специальных программ, веб-форумов и т. д.
В сборник программ элективных курсов по информатике вошли также следующие программы:
1. Технология работы с библиотечными и сетевыми ресурсами (Н.А. Коряковцева).
2. Создаём школьный сайт в Интернет (М.Ю. Монахов, А.А. Воронин).
3. Учимся проектировать на компьютере (М.Ю. Монахов, С.Л. Солодов, Г.Е. Монахова).
4. Компьютерное моделирование: сферы и границы применения (А.В. Копыльцов).
5. Информационные системы и модели (Е.К. Хеннер, И.Г. Семакин).
6. Музыкальный компьютер (новый инструмент музыканта) (И.Б. Горбунова, Г.Г. Белов, А.В. Горельченко).
При изучении элективных курсов наиболее наглядно проявляется тенденция развития современного образования, заключающаяся в том, что усвоение предметного материала обучения из цели становится средством такого эмоционального, социального и интеллектуального развития ребёнка, которое обеспечивает переход от обучения к самообразованию.
Введение элективного курса в учебный план школы может преследовать две цели. Первая - углубление профессиональной ориентации учащихся. В таком случае элективный курс является продолжением какого-то общеобразовательного курса профильного уровня по отдельным его темам (содержательным линиям). Вторая цель -удовлетворение интересов учащихся в областях знаний, не имеющих непосредственного отношения к профилю класса. Например, в классе физико-математического или технического профиля может преподаваться элективный курс гуманитарного содержания: история, искусство, языки и т.п.
Количество различных элективных курсов и их тематика теоретически неограниченны. Реальные ограничения вызваны, прежде всего, той же причиной, что и ограничения на выбор спецкурсов в вузе: с квалификацией преподавательского состава. Тематика спецкурсов, читаемых в вузе, чаще всего связана с научными интересами преподавателей. Вузовский преподаватель - это ученый, ведущий научную работу; спецкурс в вузе - это способ приобщения студентов к научно-исследовательской работе. С тематикой спецкурсов связывается и тематика курсовых и дипломных работ студентов, а это уже приближение к профессиональной деятельности.
Наиболее серьезной проблемой для школы в области профильной подготовки оказывается кадровая проблема. В обязанности школьного учителя не входит научно-исследовательская деятельность; редкие исключения лишь подтверждают правило. Разработка собственного варианта элективного курса для школьного учителя - задача весьма проблематичная. Поэтому для абсолютного большинства школьных учителей преподавание элективного курса (равно как и общеобразовательного) возможно лишь по готовым учебно-методическим разработкам.
Другой вариант решения проблемы профильного обучения (и особенно реализации элективных курсов) - использование «сетевой модели», при которой обучение элективным курсам проводится сторонними преподавателями. Это могут быть вузовские преподаватели или преподаватели, работающие в системе дополнительного образования. При этом может использоваться и материальная база этих внешних организаций: лаборатории, компьютерные классы, библиотеки. В перспективе возможно и использование дистанционных образовательных технологий.
Содержательное и методическое построение элективного курса должно отличаться от общеобразовательного курса. Как и вузовский спецкурс, элективный курс в большей степени должен ориентировать учеников на новые формы работы, приближающие их к реальному исследовательскому или производственному процессу. К особенностям методики обучения элективным курсам следует отнести:
- в большей степени ориентацию на самостоятельную работу учащихся;
- применение проблемного, деятельностного подхода к обучению;
- активное использование проектного метода.
Общеобразовательное учреждение принимает решение и несет ответственность за содержание и проведение элективных курсов в порядке, определенном учредителем.
Создание элективных курсов - важнейшая часть обеспечения введения профильного обучения. Поэтому их разработка и внедрение должны стать частью Региональных программ перехода к профильному обучению.
Глава 3. Разработка элективного курса "Компьютерное математическое моделирование"
§ 3.1 Содержание и педагогические задачи обучения элективному курсу «Компьютерное математическое моделирование»
Элективные курсы информатического содержания можно условно разделить на два типа. Первый тип - курсы со значительной теоретической компонентой, второй - практико-ориентированные курсы. Курсы первого типа связаны, прежде всего, с информационным моделированием в различных предметных областях; они развивают фундаментальную составляющую школьного базового курса информатики. Можно сказать, что курсы такого типа имеют предвузовский характер. Они стимулируют выпускника школы к продолжению обучения в вузе, развивают научные интересы, предоставляют возможность испытать себя в способности к самообучению, к решению нетривиальных задач.
Курсы второго типа ориентированы, главным образом, на изучение конкретных информационных технологий (издательские системы, компьютерная графика, мультимедиа, веб-дизайн и пр.). В результате их освоения складываются практические навыки, достаточные для применения в производственной деятельности, не требующей высшего образования.
Содержание элективного курса «Компьютерное математическое моделирование». Компьютерное математическое моделирование. Данный курс углубляет содержательную линию моделирования в курсе информатики. В нем изучается математическое моделирование в его компьютерной реализации при максимальном использовании межпредметных связей информатики и универсальной методологии моделирования. Овладение основами компьютерного математического моделирования позволит учащимся углубить научное мировоззрение, развить творческие способности, а также поможет в выборе будущей профессии. Данный раздел является преемственным по отношению к первому разделу, в котором речь также идет об информационном моделировании, но с позиций представления информации, в то время как второй раздел посвящен в основном ее математической обработке.
В ходе изучения курса должны быть расширены математические знания и навыки учащихся. В частности, рассматриваются некоторые задачи оптимизации, элементы математической статистики и моделирования случайных процессов.
Педагогические задачи изучение раздела «Компьютерное математическое моделирование». Общее развитие и становление мировоззрения учащихся. Занятие моделированием выполняет развивающую функцию, поскольку в ходе этих занятий учащиеся продолжают и углубляют знакомство с одним из важнейших методов познания окружающей действительности - методом компьютерного моделирования.
В ходе работы с компьютерными моделями приобретаются новые знания, умения, навыки. Некоторые ранее полученные при изучении информатики и других школьных предметов сведения конкретизируются и систематизируются, рассматриваются под другим углом зрения.
Овладение моделированием как методом познания. Значительный упор в курсе сделан на выработку общего методологического подхода к построению компьютерных моделей и работе с ними. Необходимо
· продемонстрировать, что моделирование в различных областях знаний имеет схожие черты, зачастую для различных процессов удается получить очень близкие модели;
· выделить преимущества и недостатки компьютерного эксперимента по сравнению с экспериментом натурным;
· показать, что и абстрактная модель, и компьютер предоставляют возможность познавать окружающий мир, управлять им в интересах человека.
Выработка практических навыков компьютерного моделирования. На примере ряда моделей из различных областей науки и практической деятельности необходимо проследить все этапы компьютерного моделирования с исследования моделируемой предметной области и постановки задачи до интерпретации результатов, полученных в ходе компьютерного эксперимента, показать важность и необходимость каждого звена. При решении конкретных задач следует выделять и подчеркивать соответствующие этапы работы с моделью. Решение данной задачи предполагает поэтапное формирование практических навыков моделирования, для чего служат учебные задания с постепенно возрастающим уровнем сложности и компьютерные лабораторные работы.
Преодоление предметной разобщенности, интеграция знаний. В рамках курса изучаются модели из различных областей науки, всякий раз с привлечением математики, что делает курс интегрированным. Для того чтобы понять суть изучаемого явления, правильно интерпретировать полученные результаты, необходимо не только владеть соответствующей терминологией, но и ориентироваться в той области знаний, где проводится модельное исследование.
Реализация меж предметных связей в данном курсе не только декларируется, как это иногда бывает в других дисциплинах, но является основой для освоения учебного материала.
Развитие и профессионализация навыков работы с компьютером. Перед учащимися ставится задача не только реализовать на компьютере предложенную модель, но и наиболее наглядно, в доступной форме, с помощью графиков и диаграмм, отобразить полученные результаты. Разработанные учащимися программы должны обладать адекватным интерфейсом, вести диалог с пользователем. Все это предполагает дополнительные требования к знаниям и умениям в области алгоритмизации и программирования, приобщает к более полному изучению возможностей современных систем программирования (в частности, весьма популярного в мире, так называемого, офисного программирования).
Формы и методы обучения элективному курсу
Основными формами учебной работы являются:
- лекционные занятия;
- теоретическое решение задач;
- лабораторные работы, выполняемые на компьютере;
- выполнение проектных заданий;
- работа над рефератами;
- защита рефератов и проектов.
В плане по изучению данной части курса, время, отводимое на теоретические и практические занятия делиться, приблизительно, поровну. К теоретической форме занятий относятся лекции и теоретическое решение задач (без выполнения на компьютере). Практическая часть - выполнение лабораторных работ, проектных заданий. Работа над рефератами осуществляется учащимися во внеурочное время.
Содержание лекций ориентируется учителем на содержание параграфов учебного пособия. В то же время, это не обязательно должен быть дословный пересказ параграфов. Там, где возможно, лекция не должна носить лишь форму монолога учителя. Как можно чаще следует использовать форму диалога с учениками, обсуждения, совместного решения проблем. Теоретические задачи - это те задания, которые приводятся в конце параграфов в учебнике. Решение их должно обсуждаться совместно всем классом.
Лабораторные работы, выполняемые на компьютере, делятся на общие и индивидуальные. На общих заданиях ученики отрабатывают определенные приемы работы. Индивидуальные задания носят творческий характер.
Индивидуальные задания связаны с выполнением проектов. Проект может выполнять как один отдельный ученик, так и группа из двух - трех (не более) человек. Вопрос о распределения проектов решает учитель. Необходимым моментом организации работы над проектами является общение между учениками. Наиболее удачно продвигающиеся работы полезно демонстрировать всем по ходу их выполнения. Такой пример поможет решить проблемы со своими проектами тем ученикам, у которых возникли затруднения.
Составной частью курса является подготовка реферата по одной из проблем, затронутых в курсе. При подборе материалов для реферата учащимся рекомендуется использование ресурсов Интернет, для его оформления потребуется работа с текстовым процессором Word и иными средствами пакета MS Office. Защиту реферата и проекта рекомендуется проводить с использованием презентации, созданной средствами Power Point.
§ 3.2 Методика преподавания отдельных тем, входящих в курс компьютерного моделирования
Обсудим методические проблемы изложения различных тем, из которых могут быть сконструированы курсы компьютерного моделирования. Порядок чередования этих тем достаточно произволен.
3.2.1 Тема «Введение в компьютерное моделирование»
Данное введение целесообразно построить в виде лекции, содержащей в доступной учащимся форме обзор основных принципов абстрактного (по другой терминологии — информационного моделирования вообще и его с помощью компьютеров. В этой беседе можно использовать, в частности, материал, изложенный в начале данной главы.
В ходе лекции учащиеся должны усвоить основополагающие знания о принципах моделирования, разновидностях компьютерного моделирования, основных этапах компьютерного моделирования.
Основные этапы компьютерного моделирования требуют обсуждения. Добиться понимания можно, в первую очередь, на примерах из общеизвестных областей реальности. Сопоставим, например, три модели самолета: детскую игрушку, натурную модель для испытания в аэродинамической трубе и абстрактную модель в видя чертежей. Все они имеют право на жизнь, но назначение у них принципиально различное, далее, могут быть и различные цели, приводящие к построению нескольких различных абстрактных моделей для последующего компьютерного моделирования: например, задачи, решаемые авиаконструктором, мало похожи на задачи, решаемые экономистом, которого заботит стоимость изделия, рентабельность производства и т.п.
Содержательное описание объекта (процесса) служит основой для дальнейшей формализации. Оно включает:
• сведения о физической природе, исследуемого объекта (процесса);
• сведения о количественных характеристиках элементарных составляющих объекта;
• сведения о месте и значении каждого элементарного явлении в общем, процессе функционирования рассматриваемой системы;
• постановку прикладной задачи, определяющей цели моделирования. Формализованная схема объекта (процесса) является промежуточным звеном между содержательным описанием и моделью и разрабатывается тогда, когда из-за сложности исследуемого процесса непосредственный переход от содержательного описания к модели затруднен. Вид формализованной схемы зависит от типа моделирования. В следующих подразделах приведено несколько примеров формализованных схем.
3.2.2 Тема «Классификационные информационные модели»
Одна из задач изучения этой темы — дать учащимся введение в системологию, сформулировать отчетливое понимание терминов «система» и «структура». Вслед за этим последует отработка как содержательных, так и технических навыков структурирования информации на уровне, принятом в современной информатике.
Вводная лекция может быть посвящена следующим вопросам:
• что такое система и структура;
• о системах искусственных и естественных;
• что такое «системный подход»;
• о системологии и информатике.
Цель этой лекции состоит в подведении учащихся к осознанию фундаментальных понятий структура и система, а также к осознанию того, что организация любой системы, выделение в ней элементов и представление вопросам, а к технологиям переходим позже, используя их как орудие реализации классификационных моделей.
На данном этапе уместно подробнее остановиться на информационных моделях, отражающих процессы возникновения, передачи, преобразования и использования информации в системах различной природы. Начать целесообразно с определения основных понятий информационного моделирования, поясняя их примерами и закрепляя путем решения задач. Вначале целесообразней разобрать пример структурирования информации путем выделения элементов (характеристик) некоторого сложного объекта. При этом целесообразно построить несколько моделей одного и тога же объекта.
Пример 1. Выделение характеристик.
Рассматриваемый объект — компьютер. Создадим несколько экземпляров описания, которые могут составить базу для построения информационной модели.
Экземпляр 1. Набор характеристик:
• фирма-изготовитель;
• место в компьютерной классификации (т.е. персональный, main-frame и т.д.);
• год изготовления;
• поколение.
Экземпляр 2. Набор характеристик:
• фирма-изготовитель;
• тип процессора;
• материнская плата;
• тип монитора;
• тип принтера.
Экземпляр 3. Набор характеристик:
• фирма-изготовитель;
• тактовая частота процессора;
• максимальная разрешающая способность монитора;
• объем ОЗУ;
• емкость винчестера.
Каждый из построенных экземпляров описания — простейшая информационная модель компьютера; совокупность экземпляров — также информационная модель. Модели эти несовершенны, так как в них нет важнейшего элемента — указания взаимосвязей между экземплярами и характеристиками.
Решение подобных задач на основе самого различного материала полезно и позволяет отработать навыки анализа, лежащего в основе построения информационных моделей.
Далее отрабатываем элементарные навыки выделения отношений между объектами, которые отражаются в информационных моделях как связи. Каждая связь задается в модели определенным именем. Связь в графической форме представляется как линия между связанными объектами и обозначается идентификатором связи.
Все связи в информационной модели требуют описания, которое включает, как минимум: идентификатор связи;
• формулировку сущности связи;
•вид связи (ее множественность и условность), способ описания связи с помощью вспомогательных атрибутов объектов.
Дальнейшее развитие представлений информационного моделирования связано с развитием понятия связи, структур, ими образуемых, и задач, которые могут быть решены на этих структурах. Так, простая последовательная структура экземпляров — не что иное как очередь (файл). Возможным обобщением являются циклическая структура, таблица, стек.
Отработку навыков моделирования с учетом связей, возникающих между характеристиками, можно начать, опираясь на знание учащимися некоторых структурированных типов данных языков программирования высокого уровня (как правило, опираясь на язык Паскаль).
Пример 2. Простейшие виды структурирования информации.
Задача ставится следующим образом. Имеется некоторая система (множество, совокупность) простых элементов (чисел, слов, знаков). Как расположить их относительно друг друга таким образом, чтобы было удобно найти потребовавшийся (произвольный) объект?
Обратите внимание учащихся, что речь идет о простом структурировании информации; задачи классификации появятся позднее. Напомните учащимся, какими свойствами отличаются стандартные структуры данных:
· упорядоченная — неупорядоченная;
· прямого доступа — последовательного доступа;
· однородная — неоднородная;
· статическая— динамическая.
Обсудите, как устроены основные структуры данных — массив, файл, запись, стек, очередь. После этого уместно провести рассуждение о том, как выбор структуры данных влияет на решение задач поиска и сортировки информации, опираясь на знания, полученные в базовом курсе.
В ходе разбора данного примера закрепляются начальные навыки классификации.
Расположение однородных данных в виде массивов и т.д. — простейший пример классификации.
С точки зрения системологии классификация есть структурирование исходного неупорядоченного
множества. В результате структурирования появляется
новое важнейшее свойство — обозримость.
Очень важную роль в информационном моделировании играет древовидная информационная модель, являющаяся одной из самых распространенных типов классификационных структур. Эта модель строится на основе связи, отражающей отношение части к целому. Очевидно, что такая связь является безусловной связью типа «один-ко-многим» и графически может быть изображена в виде дерева. Иерархическая древовидная структура естественным образом возникает, когда объекты или некоторые их свойства находятся в отношении соподчинения (вложения, наследования).
Пример 3. В задачнике есть изображение родословного дерева первых русских князей. На рис.12 изображена схема, представляющая часть этого дерева.
Обратите внимание учащихся на то, при каких обстоятельствах уместно такого рода моделирование, и на методику построения древовидных моделей. Возможность моделирования связана с наличием однозначно интерпретируемой связи «один-ко-многим». Соответствующие примеры нетрудно найти; кроме того, целесообразно задать их поиск учащимся (первым этапом может быть, например, построение генеалогического дерева собственной семьи по мужской линии).
Строится дерево, начиная с «главной» вершины — так называемого корня (или вершины первого уровня). Затем располагаются вершины второго уровня — они «подчинены» корню, но не друг другу. Их взаимосвязи друг с другом если и наличествуют, то не по тому виду связи, который положен в основу построения модели.
Рассмотренное выше дерево - это частный случай графовой структуры. В целом же графы являются мощной основой для построения информационных моделей, решения огромного числа задач информационного моделирования.
Методика построения графовых моделей подразумевает первоначальное знакомство учащихся с элементами теории графов (если это знакомство не состоялось в базовом курсе информатики).
Вначале формируется представление о графе как специальной графической форме представления информации о составе и структуре системы. Вводятся понятия о вершинах и дугах графа, об ориентированном и неориентированном графе, делается это с помощью примеров. Так, можно увязать первый из рассматриваемых примеров с обыкновенной картой дорог. На такой карте кружки — вершины графа, линии без стрелок — ребра. Расстановка стрелок была бы на таком графе неразумной, так как по дороге можно ездить в обе стороны.
Пример ориентированного графа можно дать с помощью схемы, отражающей иерархические родственные отношения, достаточно видоизменить рис. 13, и он предстанет как ориентированный граф, на котором в вершинах записаны имена князей, а ребра изображаются стрелками — от отца к сыну.
Вообще, деревом называют любой граф, в котором нет петель, т.е. связанных по замкнутой линии вершин. Так, граф, связанный с картиной дорог, нельзя представить в виде дерева, а соответствующая система не является иерархической.
Геометрические построения различных графов следует отрабатывать в процессе выполнения заданий. Многие такие задания можно найти в задачнике.
Блок-схемы алгоритмов как графы. Учитывая характер изучаемого предмета, на этом этапе уместно вспомнить правила построения блок-схем алгоритмов (при структурной алгоритмизации) и интерпретировать их как графы. На блок-схемах вершины - действия, дуги — последовательность их выполнения. При углубленном изучении графовых структур после полуэмпирической отработки основных понятий возможно подойти к вопросу более детально. При этом вводятся понятия матрицы смежности, матрицы инцидентности и матрицы достижимости (см. литературу по теории графов). Цель введения этих понятий — обсуждение вопроса о вводе информации, представленной в виден графа, в компьютер. Построение указанных матриц позволяет реализовать ввод произвольного графа в числовом виде и его последующую обработку без привлечения графических средств.
3.2.3 Тема «Логико-лингвистические информационные модели»
Под логико-лингвистической моделью понимается среда для моделирования некоторого класса объектов. В этих моделях выделяют такие компоненты, как синтаксис, семантику, логику и правила вывода.
Данная тема открывает школьникам широкие возможности для изучения вопросов, пограничных в информатике и лингвистике. Как известно, лингвистика — наука о языке. Языки можно разделить на две группы: естественные и искусственные. Естественные языки (русский, английский и т.д.) мало формализованы; тем не менее свободное описание предмета или процесса на таких языках является своеобразной моделью этого предмета или процесса. Такую модель часто называют вербальной. В определенном смысле можно считать, что любое литературное произведение есть вербальная модель того явления, о котором оно написано.
Однако не всякое моделирование (равно как и не всякий информационный процесс) следует считать объектом приложения информатики. Непременным атрибутом языка, на котором строится любая информационная модель, является наличие формализации. Эта формализация может быть очень жесткой (например, язык программирования, в котором почти всегда перестановка дух рядом стоящих символов означает или изменение смысла фразы, или ее обессмысливание); формализация может быть существенно менее жесткой (например, при использовании языка математических формул). В информатике проблемы формализации языка играют важную роль. Большинство ученых, работающих в этой сфере, считают, что любой естественный язык формализован недостаточно для того, чтобы непосредственно строить информационные модели, причастные к информатике.
Недостаточная формализация живого языка препятствует эффективному решению таких задач, как машинный перевод, распознавание смысла текстов, вводимых человеком в диалоге «человек-компьютер» (и, как следствие, невозможность создать обучающие компьютерные программы столь же эффективные, как учитель-человек).
Во вводной беседе на эту тему уместно ввести учащихся в круг проблем искусственного интеллекта, связанных с моделированием в сфере языка: представление знаний, моделирование рассуждений, компьютерная лингвистика, машинный перевод. Цель — общее развитие учащихся, привлечение их внимания к принципиальным проблемам, имеющим в то же время большое прикладное значение.
В отношении чисто логической модели представления знаний уместно ограничиться сообщением о том, что этот путь существует, но в настоящее время потеснен другими. Исчисление предикатов, лежащее в основе логического моделирования знаний, является достаточно сложной математической теорией и рассматривать его в школьном курсе нецелесообразно, тем более что в современной практике компьютерного моделирования оно почти не используется.
Обсудите методику введения в сетевые модели представления знаний. Этот способ моделирования опирается на наглядные схемы и вполне доступен. Его основная идея состоит в том, что любое знание можно представить в виде совокупности объектов (понятий) и связей (отношений) между ними. На простом примере реализуйте такое представление и переведите его в графическую форму, а затем поручите учащимся выполнить такое моделирование (на самостоятельно выбранных примерах или предложенных учителем).
Пример. Рассмотрим следующий текст: «Из гаража выпущен на линию автобус. Он работает 8 часов и возвращается в гараж. В случае неисправности он следуют в ремонтную зону».
Выделим объекты, фигурирующие в этом примере: «автобус», «гараж», «ремонтная зона». Понятия: «работать 8 часов». Отношения: «выпустить на линию», «быть исправным», «быть неисправным», «вернуться в гараж». Теперь построим представление знаний зафиксированных в этом тексте, в виде семантической сети, в которой понятия и объекты представлены в виде вершин сети, отношения — в виде линий, связывающих соответствующие вершины.
![]() В процессе построения модели
обратите внимание учащихся на то, что любой текст, описывающий реальные ситуации,
всегда можно смоделировать таким образом, для подтверждения этого предложите им
либо построить модели по представленным преподавателем текстам, либо — по собственным
(не слишком сложным).
В процессе построения модели
обратите внимание учащихся на то, что любой текст, описывающий реальные ситуации,
всегда можно смоделировать таким образом, для подтверждения этого предложите им
либо построить модели по представленным преподавателем текстам, либо — по собственным
(не слишком сложным).
Непосредственно в ходе указанных построений у учащихся возникает представление о неоднозначности выполнения задания. Оно вполне справедливо: представление (моделирование) знаний с помощью семантических сетей действительно неоднозначно, что ограничивает применимость этого вида моделирования для решения практически важных задач.
Продукционная модель представления знаний реализуется в виде ядра продукции, которое состоит из системы фраз типа «Если А то В» и некоторых вспомогательных элементов. На продукционном принципе моделирования знаний построен язык программирования Пролог, который (вместе с изучением самих принципов) вполне может быть темой профильно-ориентированного курса информатики.
Разговор о логико-лингвистических информационных моделях уместно использовать и для достижения иных, не указанных выше, общеобразовательных целей — для знакомства с компьютерной лингвистикой. Данная наука также связана с моделированием в сфере языка. Вопросы анализа текстов на естественном языке, машинного перевода, синтеза текстов на естественном языке могут стать темами для рефератов, докладов учащихся.
3.2.4 Тема «Технология компьютерного математического моделирования»
Целесообразно вводные занятия по этой теме проводить в виде беседы, привлекая знания учеников по различным общеобразовательным дисциплинам, их жизненный опыт. Изложение необходимо иллюстрировать большим количеством примеров.
Особая роль первого раздела заключается в том, что здесь потеряются и обобщаются основные понятия компьютерного математического моделирования (КММ), известные из базового курса информатики, вводятся новые понятия, такие как: «моделирование», «информационное моделирование», ''математическое моделирование», «формализация», «идентификация модели» и др.
Другой важный аспект темы – формирование представления об этапах компьютерного
математического моделирования. Здесь, с одной стороны, фигурируют ![]() приведенные выше понятия, с другой присутствует
полная технологическая цепочка КММ. Конечно, все эти этапы будут неоднократно повторяться
при исследовании конкретных процессов (объектов), но основы закладываются именно
на вводных занятиях. Действительно, одним из условий успешного усвоения учащимися
систематического курса КММ является наличие у них хорошо развитых представлений
об этапах КММ, о значении каждого из этапов.
приведенные выше понятия, с другой присутствует
полная технологическая цепочка КММ. Конечно, все эти этапы будут неоднократно повторяться
при исследовании конкретных процессов (объектов), но основы закладываются именно
на вводных занятиях. Действительно, одним из условий успешного усвоения учащимися
систематического курса КММ является наличие у них хорошо развитых представлений
об этапах КММ, о значении каждого из этапов.
Формализованная схема является промежуточным звеном между содержательным описанием и математической моделью и разрабатывается в тех случаях, когда из-за сложности исследуемого процесса переход от содержательного описания к математической модели оказывается невозможным. На этапе построения формализованной схемы должна быть дана точная математическая задача исследования с указанием окончательного перечня искомых величин и оцениваемых зависимостей.
Прежде всего составляется список величин, от которых зависит поведение объекта или ход процесса, а также список тех величин, которые желательно получить в результате моделирования.
Обозначив первые (входные) величины через x1, х2, ..., хn, а вторые (выходные) через y1, у2, ..., уk, можно поведение объекта или процесса символически представить в виде
yj = F (x1,x2,...,xn) (n=1,2,...,к),
где Fj символически обозначает некоторые математические операции над входными величинами.
Важнейшим этапом моделирования является разделение входных параметров по степени важности влияния их изменений на выходные. Такой процесс называется ранжированием. Чаще всего невозможно, да и не нужно, учитывать все факторы, которые могут повлиять на значения интересующих нас величин у. От того, насколько умело выделены важнейшие факторы, зависит успех моделирования, быстрота и эффективность достижения цели. Отбрасывание менее значимых факторов огрубляет модель и способствует пониманию главных свойств и закономерностей объекта моделирования.
На этапе перехода от формализованной схемы к математической модели необходимо перейти от абстрактной формулировки к формулировке, имеющей конкретное математическое наполнение. В этот момент модель предстанет перед нами в виде уравнения, системы уравнений, неравенств, матриц, дифференциальных уравнений и т.д.
В беседе следует подчеркнуть тот факт, что математическое моделирование отнюдь не всегда требует компьютерной поддержки. Каждый специалист, профессионально занимающийся математическим моделированием, делает все возможное для аналитического исследования модели. Аналитические решения (т.е. представленные формулами, выражающими результаты исследования через исходные данные) обычно удобнее и информативнее численных. Возможности аналитических методов решения сложных математических задач, однако, очень ограничены и, как правило, гораздо сложнее численных. Поэтому при проведении занятий по КММ в школе следует пользоваться численными методами, реализуемыми на компьютерах. Это создает определенное методическое единстве курса и заметно снижает барьер необходимой математической подготовки учащихся. Разумеется, и в численные методы при профессиональном занятии математическим моделированием приходится углубляться настолько, что при этом, требуется значительное математическое образование, но можно попытаться в школьной практике ограничиться лишь простейшими из них.
И, наконец, после изучения этого раздела учащиеся должны уяснить подходы к классификации компьютерных математических моделей. Как известно, бывают классификации моделей по используемому математическому аппарату, по отраслям наук и т.д. Наиболее органичной представляется классификация по целям моделирования. Действительно, выделение целей моделирования — это первое, что необходимо сделать перед содержательным описанием и формализацией объекта (процесса), и в конечном итоге именно цели моделирования определяют, какая модель будет построена. При этом важно подчеркнуть, что в зависимости от целей моделирования и выбранных факторов для одного и того же процесса можно получить существенно различающиеся математические модели. Учителю следует привести примеры постановки задач, приводящих к моделям, относящимся к основным классам: дескриптивным, оптимизационным, многокритериальным, игровым, имитационным.
3.2.5 Тема «Моделирование физических процессов»
Эта тема фигурирует в нескольких вариантах курса компьютерного моделирования. Причина — традиции и относительная простота решаемых задач, их близость школьному курсу физики.
Как правило, эта тема является началом к изложению компьютерного моделирования в физике. Поэтому ей может предшествовать вводная лекция (беседа) о компьютерном моделировании физических процессов в целом.
В начале на ряде примеров проиллюстрируйте утверждение, что физика — наука, в которой математическое моделирование является чрезвычайно важным методом исследования. Причину этого в целом можно сформулировать так: при максимальном проникновении в физику математических методов, порой доходящем до тактического сращивания этих наук, реальные возможности решения возникающих математических задач традиционными методами очень ограничены.
Во многих вариантах курса компьютерного моделирования математические модели в физике по праву занимают больший объем по сравнению с другими, и на их изучение отводится большее количество времени, действительно, создание той или иной модели физического процесса является естественным и не требует некоторых искусственных приемов, к которым часто приходит прибегать в других предметных областях. Поэтому восприятие этих математических описаний процессов или явлений не вызывает у учащихся, по крайней мере, психологических трудностей. В профильном курсе, ориентированном на учащихся, специализирующихся по физико-математическому и естественнонаучному профилю, целесообразно наибольшее внимание уделить именно моделям физики.
Перечень рассматриваемых вопросов может быть таков:
• движение тел с учетом сопротивления среды;
• движение маятника с учетом сопротивления среды, вынужденные колебания, резонанс и т.д.
• движение небесных тел (задача двух тел);
• движение электрических зарядов;
• тепломассоперенос (на примере процесса теплопроводности в линейном стержне).
Номенклатура компьютерных математических моделей в физике может ориентироваться на подготовленность и интересы учащихся, их специализацию в том или ином разделе физики.
Цели обучения КММ:
• дать общие представления о КММ на примере моделей из области физики;
• отработать схемы вычислительного эксперимента на сравнительно простых, знакомых по курсу физики задачах.
Поставленные задачи обучения считаются успешно выполненными, если у учащихся вырабатывается комплекс указанных ниже знаний, умений и навыков.
Изучение каждой новой содержательной задачи и, как следствие, получение новой математической модели требует мотивировки целесообразности ее введения. Мотивировка может, во-первых, опираться на жизненный опыт учащихся, во-вторых, достигаться путем разрешения проблемной ситуации. Моделирование процессов движения тел в среде. При моделировании процесса движения тела, прежде всего, целесообразно рассмотреть традиционные для школьного курса физики динамические модели, но с учетом сопротивления среды. Это свободное падение тела, полет тела, брошенного под углом к горизонту, движение тела с переменной массой. При этом составляющие силы сопротивления можно рассмотреть предварительно перед изучением конкретных моделей либо в ходе построения одной из моделей.
Более детально обсудим методику построения компьютерных математических моделей физических процессов и их последующего исследования на примере нескольких задач.
Первая из них — моделирование свободного падения тела с учетом сопротивления среды. Основная дидактическая роль этой наиболее простой задачи практическое знакомство с этапами компьютерного математического моделирования, освоение этих этапов, приобретение навыков формулирования и разрешения учебных проблем, проблемных ситуаций. Несмотря на то, что на первый взгляд она является простой, при ее исследовании придется решить ряд серьезных проблем, о чем будет сказано ниже.
В ходе обучения обязательно придется пользоваться понятиями «предел» и «производная». Понятие «предел» не вызывает существенных затруднений; в контексте данного обсуждения вполне достаточно интуитивного понимания предела, сформированного у учащихся к 10 классу.
Не совсем так обстоит дело с понятием «производная». Возможны две ситуации:
1) учащиеся вполне владеют понятием и дифференциальная форма записи второго закона Ньютона (и последующих при решении конкретных задач дифференциальных уравнений) будет им понятна (при этом никакой техники дифференцирования, тем более решения дифференциальных уравнений, не требуется);
2) учащиеся не знакомы с этим понятием; в этом случае необходимо сделать математическое отступление и пояснить понятие «производная», на что, как показывает опыт, вполне достаточно одного урока.
Другая методическая проблема, которую необходимо решить, — строить модели динамических процессов в виде дифференциальных или конечно-разностных уравнений. Как показывает практика, учащиеся физико- математических классов вполне способны воспринять дифференциальные уравнения и численные методы их решения, для этого достаточно ввести дифференциальные уравнения и объяснить простейшие численные методы их решения, базируясь на физическом и геометрическом смысле производной.
При использовании численных методов интегрирования дифференциальных уравнений разумно рассмотреть явные схемы невысокого порядка (не выше второго); если кто-либо из учащихся проявит интерес именно к методам решения систем дифференциальных уравнений и их устойчивости, то следует предложить им самостоятельно изучить литературу, где излагаются явные методы более высокого порядка либо неявные схемы. Такой подход подтвердил свою жизнеспособность.
При изучении динамических процессов в менее подготовленной аудитории рекомендуется ограничиться конечно-разностными уравнениями. Любую модель из рассмотренных ниже можно сформулировать в конечноразностном виде, вообще не упоминая о дифференциальных уравнениях (примеры далее приводятся).
Свободное падение тела с учетом сопротивления среды. В этой и многих других физических задачах, на основе которых строятся модели, фундаментальную роль играет второй закон Ньютона — снова динамики.
Приведенное рассуждение является типичным для этой темы обоснованием перехода от дискретного к непрерывному.
Далее отмечаем, что при реальных физических движениях тел в газовой или жидкостной среде трение накладывает огромный отпечаток на характер движения. Очевидно, что предмет, сброшенный с большой высоты (например, парашютист, прыгнувший с самолета), вовсе не движется равноускоренно, так как по мере набора скорости возрастает сила сопротивления среды.
Поясните учащимся, что закономерности, связывающие силу сопротивления со скоростью движения тела, носят эмпирический характер и отнюдь не имеют столь строгой и четкой формулировки, как второй закон Ньютона. Приведите эти закономерности (при этом вполне достаточно ограничиться линейной и квадратичной по скорости составляющими силы сопротивления):
![]()
Рассмотрим свободное падение с учетом сопротивления среды. Математическая модель движения — это уравнение второго закона Ньютона с учетом двух сил, действующих на тело — силы тяжести и силы сопротивления среды, движение является одномерным; проецируя векторное уравнение на ось, направленную вертикально вниз, получаем:
![]()
При выводе уравнения целесообразно изобразить на рисунке силы, действующие на тело; это будет способствовать наилучшему восприятию полученного уравнения и не вызовет дополнительных вопросов.
Вопрос, который следует обсуждать на первом этапе, таков: каков характер зависимости скорости от времени, если все параметры, входящие в последнее уравнение, заданы? При такой постановке модель носит сугубо дескриптивный характер.
На этом этапе возникает вопрос о способах решения дифференциальных
уравнений. Очевидный ответ: универсальные методы их решения — численные, для начала
вполне достаточно ограничиться методом Эйлера. Проводим следующее рассуждение: если
на основании определения производной заменить ее в уравнении (2) конечно-разностным
отношением ![]() то,
зная скорость
то,
зная скорость ![]() в начальный момент времени t=0 и обозначив ее как v1 в момент
в начальный момент времени t=0 и обозначив ее как v1 в момент ![]() , перепишем уравнение в виде
, перепишем уравнение в виде
![]()
Если далее понимать под v1 приближенное значение скорости в момент ![]() , то получим формулу
для вычисления v1:
, то получим формулу
для вычисления v1:
![]()
Это и есть формула метода Эйлера.
Далее рассуждение ведется по индукции. Располагая значением v1 можно, отталкиваясь от него, найти v2 и т.д. Общая формула метода Эйлера применительно к данной задаче такова:
![]()
Возникает следующая проблема: до каких пор проводить расчеты? В данной
задаче естественным представляется ответ: до падения тела на землю, для обнаружения
этого события необходимо рассчитывать не только скорость, но и пройденный путь.
Поскольку перемещение связано со скоростью соотношением ![]() , то, проводя схожие с приведенными
выше рассуждения, приходим ко второму разностному уравнению
, то, проводя схожие с приведенными
выше рассуждения, приходим ко второму разностному уравнению ![]() , решаемому одновременно
с первым. Иначе говоря, мы применили метод к системе дифференциальных уравнений.
Решая эту систему при заданных начальных условиях v(0) = vo, s(0) - so, получим таблицу значений
функций v(t), s(t).
, решаемому одновременно
с первым. Иначе говоря, мы применили метод к системе дифференциальных уравнений.
Решая эту систему при заданных начальных условиях v(0) = vo, s(0) - so, получим таблицу значений
функций v(t), s(t).
Важные, тесно связанные между собой методическая и содержательная проблемы
— это контроль точности и выбор шага времени ![]() . Казалось бы, чем меньше шаг, тем
точнее решение но, во-первых, это утверждение не является вполне верным (причины
обсудим ниже), а во-вторых, при очень мелком шаге расчетов «результатов» слишком
много и они становятся необозримыми. Отсюда возникает еще одна методическая проблема:
как выбрать шаг повремени для вывода значений перемещения и скорости на экран. Этот
шаг выбирается из соображений разумной достаточности информации и обозримости представления
результатов на экране; из практических соображений удобно, если он кратен
. Казалось бы, чем меньше шаг, тем
точнее решение но, во-первых, это утверждение не является вполне верным (причины
обсудим ниже), а во-вторых, при очень мелком шаге расчетов «результатов» слишком
много и они становятся необозримыми. Отсюда возникает еще одна методическая проблема:
как выбрать шаг повремени для вывода значений перемещения и скорости на экран. Этот
шаг выбирается из соображений разумной достаточности информации и обозримости представления
результатов на экране; из практических соображений удобно, если он кратен ![]() (реально шаг вывода
может составлять десятки и сотни
(реально шаг вывода
может составлять десятки и сотни ![]() ). Кроме того, ставится задача: представить
полученные результаты в наиболее удобном для восприятия виде. Это могут быта графики
зависимостей v(t), s(t), изображение процесса падениям
динамике (здесь возможны вариации).
). Кроме того, ставится задача: представить
полученные результаты в наиболее удобном для восприятия виде. Это могут быта графики
зависимостей v(t), s(t), изображение процесса падениям
динамике (здесь возможны вариации).
3.2.6 Тема «Использование компьютерного моделирования при обучении учащихся решению планиметрических задач»
Большое поле деятельности для использования компьютерного моделирования в школе представляет курс геометрии старших классов, который даёт возможность учащимся научиться моделировать реальные объекты с помощью геометрических форм и манипулировать ими в соответствии с условиями задачи.
Выполняя чертёж при решении геометрической задачи не всегда предусматривается построение отрезков по длинам, заданным в условии, а требуется только схематичное изображение фигуры и её элементов. Но в курсе геометрии встречается ряд задач, в которых при выполнении чертежа необходимо принимать во внимание соотношения между длинами рассматриваемых элементов фигуры. Приведём пример такой задачи.
В равнобедренной трапеции ABCD с основаниями AD = 17 см, BC = 5 см и боковой стороной AB = 10 см через вершину В проведена прямая, делящая диагональ АС пополам и пересекающая AD в точке М. Найдите площадь треугольника BDM [11].
При разборе задачи учащимися был выполнен чертёж, представленный на рис. 14.
Рис. 14 Чертеж трапеции
В ходе решения задачи учащиеся получают следующие значения величин: AM = 5 см, AH = 6 см, которые противоречат изображению на чертеже. Чтобы избежать этого, целесообразно провести исследовательскую работу с использованием компьютерного моделирования, направленную на выполнение чертежа.
Рассмотрим реализацию указанных выше этапов компьютерного моделирования на примере данной задачи.
На первом этапе учащиеся должны выделить существенную информацию для данной задачи: элементы фигуры и соотношения между их величинами.
На втором этапе моделирования происходит построение информационной модели. Учитываются возможности компьютерной программы, в которой будет выполнено построение чертежа. В качестве такой компьютерной программы можно использовать программу «Живая геометрия». Возможности этой программы позволяют не только строить отрезки, но и автоматически измерять их длины, находить середины отрезков, опускать перпендикуляры, что помогает установить правильное положение всех элементов фигуры.
На третьем этапе проводится исследовательская работа по выполнению правильного чертежа, который получается путём манипулирования отдельными элементами фигуры с помощью «мыши». Таким образом, проведённая работа позволяет получить следующий чертёж, представленный на рис. 15. Далее проводится работа по получению плана решения задачи и его осуществлению. На четвёртом этапе решения задачи также целесообразно использовать построенную компьютерную модель для проведения исследования решённой задачи.
Таким образом, специфика компьютерных моделей, по отношению к другим средствам обучения, состоит в том, что они являются формой научной абстракции особого рода, обеспечивающей предметно-наглядное изображение скрытых закономерностей, особым средством символизации в научно-теоретическом мышлении. Кроме того, компьютерная модель является отражением общего в изучаемых явлениях, поэтому компьютерное моделирование представляет собой не частный приём усвоения знаний, а один из общих методов познания, применяемый в самых различных областях.
§ 3.3 Разработка урока «Моделирование в электронных таблицах»
Раздел: Преподавание информатики
Урок № 1. Случайные процессы. (2 часа).
Цель урока: построить имитационную модель игры.
Учащиеся должны знать: понятие модели, случайного процесса, формализации, информационной модели, компьютерной модели, основные приемы работы в Excel, логические функции Excel, функцию случайных чисел.
Учащиеся должны уметь: работать с электронной таблицей, проводить формализацию задачи, строить информационную и компьютерную модель задачи.
План урока.
Разбор задачи "Кубики" и задачи о проверке знания таблицы умножения -объяснение у доски (40 мин).
Самостоятельная работа: задача "Домино" - работа за компьютером (40 мин).
Домашнее задание: придумать задачу о случайных процессах. Построить ее информационную модель, продумать ее реализацию в среде Excel.
Ход урока.
Задача "Кубики".
Постановка задачи.
Смоделируйте игру "Кубики": двое игроков бросают игральный кубик. Определить результат игры.
Информационная модель:
Входные параметры: х,у - очки, выпавшие у первого и второго игрока.
Выходные параметры: результат - кто победил.
Связь: если х>у, то победил первый игрок, иначе если х=у, то - ничья, иначе -победил второй игрок. Можно связь представить в виде блок-схемы.
Компьютерная модель:
|
Игра «КУБИКИ» |
||
| Имя первого игрока | Иван | |
| У первого игрока выпало: | 3 | |
| Имя второго игрока | Петр | |
| У второго игрока выпало: | 2 | |
| То есть | Выиграл первый | |
Очки, выпавшие у первого и второго игрока, выводятся только после введения имен игроков. Очистка таблицы производится клавишей F9. В ячейке первого игрока формула:
=ЕСЛИ(ЕПУСТО(В4);"";ОКРУГЛ(СЛЧИС()*6;0))
В ячейке второго игрока формула:
=ЕСЛИ(ЕПУСТО(В2);"";ОКРУГЛ(СЛЧИС()*6;0))
В ячейке результата формула:
=ЕСЛИ(ИЛИ(ЕПУСТО(В2);ЕПУСТО(В4));
ЕСЛИ (ВЗ>В5; ”выиграл, первый”; ЕСЛИ (ВЗ<В5; "выиграл второй";"ничья")))
Задача о проверке знания таблицы умножения.
Постановка задачи.
Смоделируйте работу программы проверки знания таблицы умножения. Информационная модель:
Входные параметры: х,у - сомножители, р - ответ, вводимый учеником.
Выходные параметры: результат - правильный ответ или нет.
Связь: если р=х*у, то результат - сообщение: ответ правильный, иначе - результат: сообщение об ошибке. Связь также можно представить в виде блок-схемы.
Компьютерная модель:
| Проверка таблицы умножения | ||||
| Чему равно произведение | 4 | * | 6 | ? |
| Ваш ответ | 15 | |||
| Ошибка | ||||
Для вычисления сомножителей применяются формулы:
=ОКРУГЛ(СЛЧИС()*9;0)
Для проверки результата используется формула:
=ЕСЛИ(ИЛИ(ЕПУСТО(В2);ЕПУСТО(D2);ЕПУСТО(ВЗ));"";ЕСЛИ(В2*D2=ВЗ;"правильно";"ошибка"))
Самостоятельная работа.
Постановка задачи:
Смоделируйте выбор наугад двух костей домино из полного набора костей этой игры (0-0, 0-1, ..., 6-6). Определить, можно ли приставить эти кости одна к другой в соответствии с правилами домино.
Информационная модель:
Входные параметры: х1,у1,х2,у2 - значения костей домино.
Выходные параметры: ответ: можно приставить кости одну к другой или нет. Связь: если xl=x2 или xl=y2 или yl=x2 или yl=y2, то ответ: можно, иначе - ответ: нельзя. Связь можно представить в виде блок-схемы.
Компьютерная модель:
Для получения значений "костей" домино используются формулы:
=ОКРУГЛ(СЛЧИС()*6;0)
Для определения результата используется формула:
=ЕСЛИ(ИЛИ(В2=ВЗ;В2=ОЗ;О2=ВЗ;О2=ОЗ);"можно";"нельзя")
§ 3.4 Задания для самостоятельной работы
1. Моделирование в среде графического редактора
Задания для самостоятельной работы
1. Построить прямоугольный треугольник по гипотенузе и катету. Построение произвести по нижеприведенному или собственному алгоритму.
- Угол, вписанный в окружность и опирающийся на диаметр, равен 90. приведенный на рисунке алгоритм основан на построении двух окружностей: с диаметром, равным заданной гипотенузе, и с радиусом, равным заданному катету.
2. Построить равнобедренный треугольник по боковой стороне и углу при вершине. Построение произвести по собственному алгоритму.
3. Построить треугольник по трем сторонам.
4. Построить восьмиугольник с заданной стороной.
5. Построить параллелограмм по заданным сторонам и острому углу.
6. Построение 3 проекций по общему виду объекта.
7. Создать с помощью компьютера план известного вам исторического сражения.
8. Создать собственную галерею мод, используя в качестве модели нарисованную фигурку человека.
9. Создать экранный набор плоских или объемных деталей для моделирования православных храмов и церквей, строящихся по определенным канонам. При создании меню желательно использовать знания, полученные на уроках истории или дополнительную литературу.
10. Разработать эскизы базовых элементов и на их основе создать узор для деревянной поделки – шкатулки, доски или рамки.
2. Моделирование в среде текстового редактора
Задания для самостоятельной работы
1. Наградной диплом. При проведении различных конкурсов одной из форм поощрения участников являются наградные дипломы. Они должны быть заверены подписью официальных лиц (председателя и членов жюри). Иногда диплом может подтверждать шуточные достижения. Создайте и оформите эскиз диплома.
2. Объявление. Это документ который содержит некоторую информацию. По своему содержанию объявления могут быть разные:
- Объявление о предстоящем концерте, встрече, собрании содержит информацию о дате, времени, месте и теме события;
- Объявление о пропаже содержит характеристики объекта, контактный телефон;
- Объявление об услугах, пропаже, обмене содержит характеристику объекта в наиболее привлекательном виде.
Составьте эскиз объявления на выбранную тему.
3. Составить фрагмент расписания, состоящего из четырех уроков и удовлетворяющих следующим требованиям:
- Математика должна быть первым или вторым уроком пока ученики еще не устали;
- Физкультура может быть только последней, чтобы разгоряченные школьники сразу шли домой;
- Историю можно ставить первым, вторым или третьим уроком;
- Учитель литературы может дать второй или третий урок.
4. Составить алгоритмическую модель нахождения наибольшего общего делителя двух чисел.
5. Составить алгоритмическую модель умножения двух чисел А и В с определением знака произведения.
6. Составить алгоритмическую модель определения возможности построения треугольника по трем заданным сторонам А, В, С. Оформить комплексный отчет, включающий элементы оформления, текст задания, алгоритмическую модель в виде блок-схем.
7. Чтобы предупредить развитие болезней, помидоры и огурцы опрыскивают бордоской жидкостью – смесью растворов медного купороса и извести. Главное условие при использовании такой жидкости – раствор не должен быть кислотным. Проверяется раствор лакмусовой бумажкой. Есть три варианта реакции: бумажка покраснела (кислотная реакция), посинела (щелочная), или не изменила цвет (нейтральная). Составить алгоритмическую схему принятия решения об опрыскивании растений бордоской жидкостью.
8. Составить алгоритмическую схему правила «Частица НЕ с прилагательными».
|
Частица НЕ с прилагательными |
|
| СЛИТНО | РАЗДЕЛЬНО |
| Если без НЕ не употребляется | Если имеется (или подразумевается) противопоставление |
| Если образует новое слово (которое часто можно заменить близким по смыслу без НЕ) |
Если отрицание усиливается отрицательными местоимениями или отрицательными наречиями, а также если входит в состав частиц далеко не, вовсе не, отнюдь не |
|
Если употребляется со словами совсем, совершенно, весьма, чрезвычайно и др., усиливающими степень качества |
Если употребляется с краткими прилагательными, которые не имеют полной формы, или у которых она имеет иное значение |
3. Моделирование в электронных таблицах
Задания для самостоятельной работы
1. Определение максимальной площади треугольника. В прямоугольном треугольнике задана длина гипотенузы с. Найти размеры катетов, при которых треугольник имеет наибольшую площадь. Составить геометрическую и математическую модель. Провести расчеты.
2. Определение минимальной длины изгороди садового участка. Садовый участок прямоугольной формы имеет площадь S. При каких размерах длины и ширины участка длина изгороди будет наименьшей? Составьте геометрическую и математическую модель. Провести расчеты.
3. Продукты для похода. Для организации похода надо построить модель расчета нормы продуктов для группы туристов. Известна норма каждого продукта на 1 человека на день, количество человек и количество дней похода.
| Продукты для похода | |
| Количество человек | 15 |
| Количество дней | 6 |
| Название | 1 человек/день |
| Вермишель г. | 55 |
| Рис, г. | 20 |
| Пшено, г. | 20 |
| Гречка, г. | 20 |
| Картофель, г. | 200 |
| Колбаса, г. | 40 |
| Сыр, г. | 50 |
| Масло, г. | 35 |
| Суп, пакет | 0,33 |
| Хлеб, шт. | 0, 33 |
| Булка, шт. | 0,33 |
| Чай, г. | 5 |
| Кофе, г. | 5 |
| Сахар, г. | 30 |
| Сушки, г. | 50 |
| Конфеты | 20 |
4. Буратино и папа Карло. У папы Карло было накоплено 20 золотых, когда Буратино поступил на работу в кукольный театр Карабаса Барабаса. Ежедневно Буратино приносил зарплату 5 золотых, а папа Карло тратит половину (50%) имеющегося на начало недели богатства. Постройте модель изменения капитала в течении нескольких недель. Исследуйте модель и ответьте на вопросы:
- Как изменяется капитал, если увеличить (уменьшить) начальный капитал папы Карло?
- Как изменяется капитал, если увеличить (уменьшить) зарплату Буратино?
- Как изменяется капитал, если увеличить (уменьшить) процент еженедельной траты капитала?
5. Аквариум. Мальчик решил почистить аквариум. Начал с переселения рыб в банку. Семейство рыб, проживающих в аквариуме, составляло 40 штук. Первую рыбку он поймал быстро, затратив 5 с., и еще 2с. потратил на перекладывание в банку. Но чем меньше становилось в воде рыбок, тем труднее было их поймать. На каждую следующую рыбку он затрачивал времени больше на 5% , чем на предыдущую. Сколько минут времени он затратит на переселение рыбок?
6. Награда. Шахматы были изобретены в Индии. Индусский царь Шерам решил наградить изобретателя шахмат, вызвал его к себе и сказал, что исполнит любую его просьбу. Изобретатель удивил царя беспримерной скромностью просьбы: - Прикажи выдать мне за первую клетку шахматной доски 1 пшеничное зерно, за вторую – 2, за каждую следующую в два раза больше, чем за предыдущую. Сколько килограммов зерна было выдано изобретателю, если 1 зерно весит 0,05г.?
7. Обработка массива оценок. Исследуйте массив оценок в классном журнале за ограниченный промежуток времени [11]. Проделайте два эксперимента:
- с массивом, содержащим оценки одного ученика по разным предметам;
- с массивом оценок всего класса по одному предмету.
Виды обработки придумайте самостоятельно.
8. Совместимость людей по биоритмам. Когда у двух людей совпадают или очень близки графики по одному, двум или даже всем трем биоритмам, то можно предложить довольно высокую совместимость этих людей. Построить модель физической, эмоциональной и интеллектуальной совместимости двух друзей.
9. Спасение утопающего. С какой скоростью и под каким углом надо бросить с борта спасательного судна круг утопающему? При расчетах учесть следующие условия:
1. начальная скорость может изменяться в пределах до 10 м/сек;
2. расстояние утопающего от корабля;
3. точность попадания равна 0,5м;
4. угол бросания может быть отрицательным;
5. высоту борта корабля над уровнем моря.
10. Кроличья семья. Самка кролика каждые два месяца приносит в среднем 10 крольчат. Провести расчет пополнения кроличьей семьи молодняком в течении года.
11. Лотерея «Спортлото». Кто из вас не знает лотерею «Спортлото»? существует две распространенных тактики:
1. зачеркивать в билетах одну и ту же комбинацию из «счастливых» чисел;
2. бросать кубик и из количества точек на верхней грани составлять набор чисел.
Наберите статистику. Сделайте выводы.
Информационные основы процессов управления
Информационная модель объекта
Тема для дискуссии:
Можно ли один объект описать с помощью разных информационных моделей? Если да, то чем они будут отличаться?
Задания для самостоятельной работы.
1. Составить информационную модель «самолет» с целью характеристики его пассажиров. Как изменится модель, если цель – характеристика самолета как технического устройства?
2. Составьте информационные модели объекта «арбуз» для разных целей: нарисовать рисунок, выбрать самый вкусный, вырастить.
3. Приведите примеры моделей, созданных с разной целью.
4. Приведите примеры моделей технических устройств.
Представление о системе объектов. Основы классификации объектов
Тема для дискуссии:
Какими сравнительными характеристиками можно описать отношения части и целого? Приведите примеры.
Задания для самостоятельной работы.
1. Приведите примеры географических связей.
2. Придумайте системы, которые можно построить из объектов «доски», «гвозди».
3. Составьте таблицу отношений однотипных объектов «товары»
4. Назовите характеристики системы в целом и ее составляющих (свойства, действия) для объектов «стол», «класс учащихся».
5. составьте информационные модели систем «классная комната», «садовый участок».
6. Назовите основание, по которому в одну группу могли бы попасть следующие объекты:
- Кенгуру, утконос, кролик, броненосец;
- Роза, колесо, футбольные бутсы, кактус;
- Молоко, бензин, кислота, магма.
7.Классифицируйте домашнюю посуду по следующим признакам; материал, назначение, долговечность.
Классификация моделей
Тема для дискуссии:
К какому типу моделей можно отнести былины? Что они моделируют?
Задания для самостоятельной работы.
1. Привести примеры математических моделей.
2. Привести примеры применяемых в школе учебных моделей.
3. Можно ли стратегическую компьютерную игру назвать игровой моделью? Чему учат такие игры?
4. Привести примеры компьютерных моделей.
Основные этапы моделирования
Тема для дискуссии:
Какие ошибки встречаются в процессе моделирования? Что надо делать, когда ошибка обнаружена?
Задания для самостоятельной работы.
1. В известном «Задачнике» Г. Остера есть следующая задача: Злая колдунья, работая не покладая рук, превращает гусениц по 30 принцесс в день. Сколько дней ей понадобится, чтобы превратить в гусениц 810 принцесс? Сколько принцесс в день придется превращать в гусениц, чтобы управиться с работой за 15 дней? Какой вопрос можно отнести к типу «что будет, если…», а какой – к типу «как сделать, чтобы…»?
2. Формализуйте шутливую задачу из «Задачника» Г. Остера: Из двух будок, находящихся на расстоянии 27 км. Одна от другой, навстречу друг другу выскочили в одно и тоже время две драчливые собачки. Первая бежит со скоростью 4 км/час, а вторая – 5км/час. Через сколько времени начнется драка?
3. Назовите как можно больше характеристик объекта «пара ботинок». Составьте информационную модель объекта для разных целей:
a. выбор обуви для туристского похода;
b. подбор подходящей коробки для обуви;
c. покупка крема для ухода за обувью
Заключение
На основании вышеизложенного мы пришли к выводу, что информационные и коммуникационные технологии (ИКТ) – это обобщающее понятие, описывающее различные устройства, механизмы, способы, алгоритмы обработки информации. Важнейшим современным устройствами ИКТ являются компьютер, снабженный соответствующим программным обеспечением и средства телекоммуникаций вместе с размещенной на них информацией. С помощью ИКТ решаются следующие дидактические задачи: совершенствование организации преподавания, повышение индивидуализации обучения; повышение продуктивности самоподготовки учащихся; индивидуализация работы самого учителя; ускорение тиражирования и доступа к достижениям педагогической практики; усиление мотивации к обучению; активизация процесса обучения, возможность привлечения учащихся к исследовательской деятельности; обеспечение гибкости процесса обучения.
Элективные курсы, хотя и различаются по целям и содержанию, должны соответствовать запросам учащихся, которые их выбирают. Элективные курсы как бы «компенсируют» во многом достаточно ограниченные возможности базовых и профильных курсов в удовлетворении разнообразных образовательных потребностей старшеклассников.
Содержание курса информатики старшей школы направлено на развитие у старшеклассников основ системного видения мира, на комплексное освоение возможностей информационного моделирования в практической деятельности. Оценивая возможность и педагогическую целесообразность введения тех или иных элективных курсов информатики, необходимо учитывать такие важные задачи, как формирование умений и способов деятельности для решения практически важных задач, приобретение образовательных результатов для успешного продвижения на рынке труда, продолжение профориентационной работы, осознание возможностей и способов реализации выбранного жизненного пути.
Модели по своей сути - чисто информационное понятие. Модели - это отражение наиболее существенных признаков, свойств и отношений явлений, объектов или процессов предметного мира. Различают четыре основных вида модельных представлений: графические представления, словесные описания, информационно-логические модели, математические (количественные) модели.
Метод моделирования широко используется во всех областях человеческой деятельности, в том числе и в учебной. Знакомство учащихся с элементами математического и компьютерного моделирования способствует не только формированию у них научного мировоззрения, но и делает их учебную деятельность более осмысленной и продуктивной.
Мы пришли к выводу, что специфика компьютерных моделей, по отношению к другим средствам обучения, состоит в том, что они являются формой научной абстракции особого рода, обеспечивающей предметно-наглядное изображение скрытых закономерностей, особым средством символизации в научно-теоретическом мышлении. Кроме того, компьютерная модель является отражением общего в изучаемых явлениях, поэтому компьютерное моделирование представляет собой не частный приём усвоения знаний, а один из общих методов познания, применяемый в самых различных областях.
Также в данной работе мы привели ряд методических рекомендаций по использованию информационных технологий в обучении информационному моделированию учащихся старших классов в рамках элективного курса информатики, которые подробно описаны во второй и третьей главе.
Библиография
1. Бахвалов, Л. Компьютерное моделирование: долгий путь к сияющим вершинам? [Текст] / Л. Бахвалов // Компьютерра. - 1997. - № 40. - С.15-25.
2. Бирюков, Б.В. Моделирование. [Текст] / Б.В. Бирюков, Ю.А. Гастеев, Е.С. Геллер. - М.: БСЭ, 1994. - 252с.: ил
3. Возрастная и педагогическая психология: Учебное пособие для студентов пед. ин-тов [Текст] / Под ред. А.П. Петровского. - М.: Просвещение, 1973. - 288с.: ил.
4. Гейн, А.Г. Информатика. 7-9 класс: Учебник для общеобразовательных учреждений. [Текст] / А.Г. Гейн, А.И. Сенокосов, В.Ф. Шолохович. - 8-е изд., стер. - М.: Дрофа, 2005. - 240с.: ил.
5. Гейн, А.Г. Основы информатики и вычислительной техники: Проб. учеб. для 10 - 11 кл. общеобразоват. учреждений [Текст] / А.Г. Гейн, В.Г. Житомирский, Е.В. Линецкий. - 5-е изд. - М.: Просвещение: Моск. учебники, 1996. - 254с.: ил.
6. Гультяев, А. Визуальное моделирование в среде MATLAB: Учебный курс. [Текст] / А. Гультяев. - СПб.: Питер, 2000. - 432с.: ил.
7. Дименштейн, Р.П. Информатика или компьютерное дело. [Текст] / Р.П. Дименштейн, А.Г. Яковлев. // Информатика и образование. - 1989. - № 3. - С. 5-27.
8. Добрович, А.Б. Воспитателю о психологии и психогигиене общения. [Текст] / А.Б. Добрович. - М.: Просвещение, 1987. - 274с.
9. Ершов, А.П. Основы информатики и вычислительной техники: Пробное учебное пособие для средних учебных заведений: В 2 ч. [Текст] / Под ред. А.П. Ершова и В.М. Монахова. - М.: Просвещение, 1996.
10. Иванова, А.Ю. Практическое моделирование. Компьютерный эксперимент. Лабораторный практикум: Учебное пособие [Текст] / А.Ю. Иванова. - Томск: Том. гос. ун-т систем управления и радиоэлектроники, 2005.
11. Иванова, А.Ю. Практическое моделирование. Компьютерный эксперимент. Методические указания для преподавателя [Текст] / А.Ю. Иванова. - Томск: Том. гос. ун-т систем управления и радиоэлектроники, 2005.
12. Кон, И.С. Психология старшеклассника. Пособие для учителей [Текст] / И.С. Кон. - М.: Просвещение, 1980. - 192с.
13. Концепция профильного обучения на старшей ступени общего образования: Уч.-метод. пособие для учителей общеобр. шк. [Текст] / Под ред. Г.К. Селевко. - М.: Академия, 2003. - 22с.
14. Кузнецов, А.А. Элективные курсы в профильном обучении: Образовательная область «Информатика» [Текст] / М-во образования РФ. – Нац. фонд подготовки кадров; А.А. Кузнецов. - М.: Вита-Пресс, 2004. - 132с.
15. Кушниренко, А.Г. Основы информатики и вычислительной техники: Учебник для 10-11 кл. средней шк. [Текст] / А.Г. Кушниренко, Г.В. Лебедев, Р.А. Сворень - М.: Просвещение, 2000. - 224с.
16. Макарова, Н. В. Информатика: 9 кл. [Текст] / Н.В. Макарова. - СПб.: Питер, 2001. - 304с.: ил.
17. Макарова, Н.В. Информатика: 10-11 кл. [Текст] / Под ред. Н.В. Макаровой.- СПб.: Питер, 2002. - 304с.: ил
18. Математическое моделирование: Пособие для учителя. [Текст] / О.А. Церенова. - Пермь: Перм. гос. пед. ун-т, 1995. - 259с.
19. Могилев, А.В. Элементы математического моделирования. [Текст] / Под ред. А.В. Могилева, И.Я. Злотникова. - Омск: ОМГПУ, 1995. - 104с.
20. Сайдашев, А.А. Некоторые вопросы современной подготовки учителя математики в связи с компьютеризацией [Текст] / А.А. Сайдашев, Е.К. Хеннер, А.П. Шестаков // Педагогическая информатика. -1993. - № 1. - С. 37-43.
21. Семакин, И.Г. Информатика: Базовый курс: 7-9 кл. [Текст] / И.Г. Семакина.- М.: БИНОМ. Лаб. Знаний, 2002.- 384с.: ил.
22. Семакин, И.Г. Информатика: Задачник-практикум: в 2 т. [Текст] / Под ред. И.Г. Семакина, Е.К. Хеннера. - М.: БИНОМ. Лабо. Знаний, 2004. - 278с.: ил.
23. Стандарт среднего (полного) образования по информатике и информационным технологиям. Базовый уровень. Профильный уровень [Текст] / Под ред. А.Г. Шмелева // Информатика и образование. - 2004. - № 4. - С. 2-29.
24. Шестаков, А.П. Интегрированный курс "Математическое моделирование" в подготовке учителя математики и информатики [Текст] / А.П. Шестаков // Подготовка преподавателя математики и информатики для высшей и средней школы: Тез. докл. межд. конф. - М.: МПГУ, 1994. Ч. 2. - С. 78-80.
25. Шестаков, А.П. Математическое моделирование в школе [Текст] / А.П. Шестаков // Информатизация образования - 93: Тез.докл. научно-практ. конф. Екатеринбург: Изд-во Уральского ГПУ, 1993. - С. 12-13.
26. Шестаков, А.П. Преподавание курса "Математическое моделирование" в средней школе [Текст] / А.П. Шестаков // Математическое моделирование систем и явлений: Тез. докл. Межрегиональной научно-техн. конф. - Пермь: ПГТУ, 1993. - С. 8-139.