
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по муниципальному праву
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Доклад: Графика в системе Maple V
Доклад: Графика в системе Maple V
1. Двумерная графика
1.1. Основные возможности двумерной графики
Лидером по графическим возможностям среди математических систем для персональных компьютеров долгое время считалась система Mathematics 2. Однако в реализации Maple V R4 возможности графики системы Maple V приблизились к таковым у системы Mathematica 2 и даже Mathematica 3. Они настолько обширны, что, будь математическая графика Maple V единственным назначением системы, оно вполне оправдало бы ее разработку.
Графика Maple V реализует все мыслимые (и даже «немыслимые») варианты математических графиков — от построения графиков простых функций в Декартовой и в полярной системах координат до создания реалистических образов сложных пересекающихся в пространстве фигур с их функциональной окраской. Возможны наглядные графические иллюстрации решений самых разнообразных уравнений, включая системы дифференциальных уравнений.
В само ядро Maple V встроено ограниченное число функций графики. Это прежде всего функция для построения двумерных графиков (20-типа) — plot и функция для построения трехмерных графиков (ЗО-типа) — plot3d. Они позволяют строить графики наиболее распространенных типов. Для построения графиков специального типа (например, в виде векторных полей градиентов, решения дифференциальных уравнений, построения фазовых портретов и т.д.) в пакеты расширения системы Maple V включено большое число различных графических функций. Для их вызова необходимы соответствующие указания.
Вообще говоря, средства для построения графиков принято считать графическими процедурами или операторами. Однако мы сохраним за ними наименование функций в силу двух принципиально важных свойств:
• графические средства Maple V возвращают некоторые графические объекты, которые размещаются в окне документа в строке вывода или в отдельном графическом объекте;
• эти объекты можно использовать в качестве значений переменных, т.е. переменным можно присваивать значения графических объектов и выполнять над ними соответствующие операции (например, с помощью функции show выводить на экран несколько графиков).
Графические функции заданы таким образом, что обеспечивают построение типовых графиков без какой-либо особой подготовки. Все, что для этого нужно, это указать функцию, график которой строится, и пределы изменения независимых переменных. Однако с помощью дополнительных необязательных параметров — опций можно существенно изменить вид графиков, например, изменить стиль и цвет линий, вывести титульную надпись, изменить вид координатных осей и т.д.
13.1.2. Основная функция двумерной графики — plot
Для построения двумерных графиков служит функция plot. Она задается в виде:
plot(f, h, v) или plot(f, h, v, о),
где f — функция (или функции), чей (чьи) график(и) строятся, h — переменная с указанием области ее изменения по горизонтали, v — заданная опционально переменная с указанием области изменения по вертикали, о — опция или набор опций, задающих стиль построения графика (толщину и цвет кривых, тип кривых, метки на них и т.д.).
Самыми простыми формами задания этой функции служат:
plot(i,xmin..xmax) — построение графика функции f, заданной только именем;
plot(f(x),x=xrnin..xmax) — построение графика функции f(x).
Диапазон изменения независимой переменной х задается как xmin..xmax, где xmin и гпах — минимальное и максимальное значение х, .. (две точки) — составной символ, указывающий на изменение независимой переменной. Разумеется, имя х здесь дано условно — независимая переменная может иметь любое допустимое имя.
Для двумерной графики возможны следующие опции:
| axes | Вывод различных типов координат (axes=NORMAL — обычные оси, выводятся по умолчанию, axes=BOXES — график заключается в рамку с оцифрованными осями, axes=FRAME — оси в виде перекрещенных линий и axes=NONE — оси •не выводятся). |
| color | Задает цвет кривых (см. далее). |
| coords | Задание типа координатных систем (см. далее). |
| numpoints | Задает минимальное количество точек графика (по умолчанию numpoints=49). |
| resolutions | Задает горизонтальное разрешение устройства вывода (по умолчанию resolutions-200, параметр используется при отключенном адаптивном методе построения графиков). |
| scaling | Задает масштаб графика CONSTRAINED (сжатый) или UNCONSTRAINED (несжатый — по умолчанию). |
| size | Задает размер шрифта в пунктах. |
| style | Задает стиль построения графика (POINT — точечный, LINE — линиями). |
| symbol | Задает вид символа для точек графика (возможны значения BOX — прямоугольник, CROSS — крест, CIRCLE — окружность, POINT — точка, DIAMOND — ромб). |
| title | Задает построение заголовка графика (title=«string», где string — строка). |
| titlefont | Определяет шрифт для заголовка (так же как и для font). |
| labelfont | Определяет шрифт для меток (labels) на осях координат (так же как и для font). |
| thickness | Определяет толщину линий графиков (0, 1,2,3, по умолчанию 0). |
| view=[A, B] | Определяет максимальные и минимальные координаты, в пределах которых график будет отображаться на экране, А = [xmin..xmax], B=[ymin..углах] (по умолчанию отображается вся кривая). |
| xtickmarks | Задает минимальное число отметок по оси X. |
| ytickmarks | Задает минимальное число отметок по оси Y. |
В основном задание параметров особых трудностей не вызывает. За исключением задания титульной надписи с выбором шрифтов по умолчанию — в этом случае не всегда поддерживается вывод символов кириллицы (русского языка). Подбором подходящего шрифта эту проблему удается решить.
13.1.3. Задание координатных систем 20-графиков и их пересчет
В версии Maple V R4 параметр coords задает 15 типов координатных систем для двумерных графиков. По умолчанию задана прямоугольная (Декартовая) система координат (coords=cartesian). При использовании других координатных систем координаты точек для них (u,v) преобразуются в координаты (х,у) как (u, v) -> (x, у). Ниже приведены наименования систем координат (значении параметра coords) и соответствующие формулы преобразования:
bipolar
х = sinh(v)/(cosh(v)-cos(u)) у = sin(u)/(cosh(v)-cos(u))
cardiod
х = [/2*(u'2-v~2}/(u'2+v'2Y2 у = u*v/(ir2+v"2)-2
cartesian
х = u у = v
cassinian
x = a*2«(l/2)/2*((exp(2*u)+2*exp(l^)*cos(v)+l)«(l/2) +
exp(u)*cos(v)+l)"(l/2) у = a*2»(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+l)"(l/2) -
exp(u)*ws(v)-l)'-(\/2)}
elliptic
x = cosh(u)*cos(v) у = sinh(u)*sin(v)
hyperbolic
x = ((iT2+v-2)-(l/2)+u)-(l/2) у = ((^2+у'2Г(\/2)-иУ(1/2)
invcassinian
x = a*2~(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+l)"(l/2) +
exp(u)*cos(v)+l)»(l/2)/(exp(2*u)+2*exp(u)*cos(v)+l)-(l/2) у = a*2»(l/2)/2*((exp(2*u)-^2*exp(u)*cos(v)+l)-(l/2) -
exp(u)*cos(v)-l)»(l/2)/(exp(2*u)+2*exp(u)*cos(v)+l)-(l/2)
invelliptic
x = a*cosh(u)*cos(v)/(cosh(u)"2-sin(v)'2) у = a*sinh(u)*sin(v)/(cosh(u)"2-sin(v)»2)
logarithmic
x = ii/Pi*ln(u'2+v'2) у = 2*a/Pi*arctan(v/u)
logcosh
x = a/Pi*\n(c.osh(uy2-sm(vy2} у = 2*a/Pi*arctan(tanh(u)*tan(v))
maxwell
x = a/Pi*(u+l+exp(u)*cos(v)) у = a/Pi*(v+exp(u)*sin(v))
parabolic
x = (u'2-v^2)/2 у = u*v
I'I-
polar
x = u*cos(v) у = u*sin(v)
rose
x = ((u'2+v'2Y(\/2)+ur(\/2)/(u~2+v'2)-(i/2) у = ((^2+v'2)-(\/2)-u)-(\/2)/(u'2+^2r(\/2)
tangent
x= u/tu^+v^) у = v/(iT2+v'2)
13.1.4. Управление стилем и цветом линий 20-графиков
Maple V R4 позволяет воспроизводить на одном графике множество кривых. При этом возникает необходимость из выделения. Для этого можно использовать построение линии разными стилями и разными цветами и разной толщиной линий. Набор средств выделения кривых позволяет уверенно различать их как на экране цветного дисплея и распечатках цветным струйным принтером, так и при печати монохромными принтерами.
Параметр style позволяет задавать следующие стили для линий графиков:
SPISV = POINT или point — график выводится по точкам;
LINE или line — график выводится линией.
Если задано построение графика точками то параметр symbol позволяет представить точки в виде различных символов, например, прямоугольника, креста, окружности или ромба.
Другой параметр color позволяет установить обширный набор цветов линий графиков:
aquamarine black blue navy coral cyan brown gold green gray grey khaki magenta maroon orange pink plum red sienna tan turquoise violet wheat white yellow
Различные цветовые оттенки получаются использованием RGB-комбинаций базовых цветов: red — красный, green — зеленый, blue — синий. Приведем перевод ряда других комбинированных цветов: black — черный, white — белый, khaki — цвет «хаки», gold — золотистый, orange — оранжевый, violet — фиолетовый, yellow — желтый и т.д. Перевод цветов некоторых оттенков на русский язык не всегда однозначен и потому не приводится. Средства управления стилем графиков дают возможность легко выделять различные кривые на одном рисунке, даже если для выделения не используются цвета.
13.2. Примеры построения основных типов 20-графиков
13.2.1. Построение графиков одной функции
При построении графика одной функции она записывается в явном виде на место шаблона f. Примеры построения графика одной функции представлены на рис. 13.1. Обратите внимание на то, что график функции sin(x)/x строится без
характерного провала в точке х=0, который наблюдается при построении графиков этой функции многими программами. Он связан с используемым в них правилом — функция задается равной нулю, если ее числитель равен нулю. Данная функция в этой точке дает устранимую неопределенность 0/0->1, что и учитывает графический процессор системы Maple V.
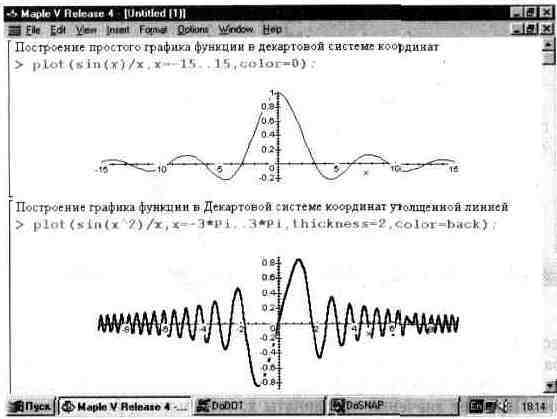
Рис. 13.1. Примеры построения графиков одной функции.
При построении графиков одной функции могут быть введены указатели масштабов и различные опции, например задания цвета кривой, толщины линии, которой строится график функции и другие параметры. К примеру, запись в списке параметров со1ог=0 (не документированная возможность) или запись color=black задают вывод кривых черным цветом, а запись thinkness=2 задает во втором примере рис. 13.1 построение графика линией, удвоенной в сравнении с обычной толщиной.
13.2.2. Управление масштабом графиков
Для управления масштабом графиков служат указатели масштабов. В ряде случаев их можно не применять и система автоматически задает приемлемые масштабы. Однако их явное применение позволяет задать масштаб «вручную». Иногда соответствующее задание масштаба случайно или целенаправленно ведет к отсечению части графика — например на рис. 13.2 в первом примере отсечена верхняя часть графика.
Правильный выбор масштаба повышает представительность графиков функций. Рекомендуется вначале пробовать строить такие графики с автоматическим масштабированием, а уже затем использовать указатели масштабов.
13.2.3. Графики функций в неограниченном масштабе
Изредка встречаются графики функций цх), которые надо построить при изменении значения х от нуля до бесконечности или даже от минус бесконечности до
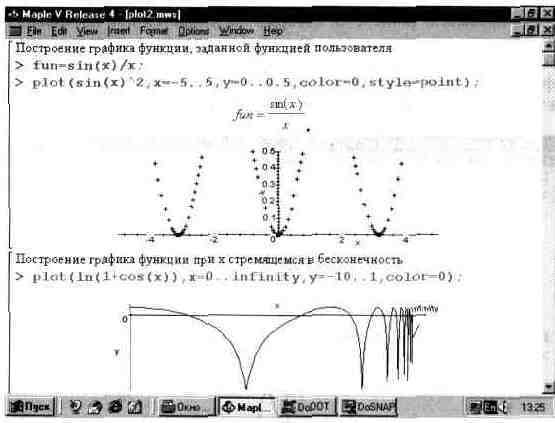
Рис. 13.2. Построение графиков функции с явным указанием масштаба.
плюс бесконечности. Бесконечность в таких случаях задается в указателях масштаба как особая константа infinity. В этом случае масштаб автоматически меняется по ходу построения графика. Рис. 13.2 (второй пример) иллюстрирует сказанное. Пересчет значении координаты х, устремляющейся в бесконечность, выполняется с помощью функции для арктангенса.
13.2.4. Графики функций с разрывами
Некоторые функции, например tan(x), имеют при определенных значениях х разрывы, причем случается что значения функции в этом случае устремляются в бесконечность. Функция tan(x), к примеру, в точках разрывов устремляется к +°° и -°°. Построение графиков таких функций нередко дает плохо предсказуемые результаты. Графический процессор Maple V не всегда в состоянии определить оптимальный масштаб по оси ординат, а график функции выглядит весьма непредставительно — если не сказать безобразно (см. рис. 13.3 — первый пример).
Среди параметров функции plot есть специальный параметр discont. Если задать его значение равным true, то качество графиков существенно улучшается — см. рис. 13.3 — второй пример. Улучшение достигается разбивкой графика на несколько участков, в которых функция непрерывна, и более тщательным контролем за масштабом.
13.2.5. Построение графиков нескольких функций на одном рисунке
Важное значение имеет возможность построения на одном рисунке графиков нескольких функций. В простейшем случае (рис. 13.4 первый пример) для построения таких графиков достаточно перечислить нужные функции и установить для них общие масштабы.
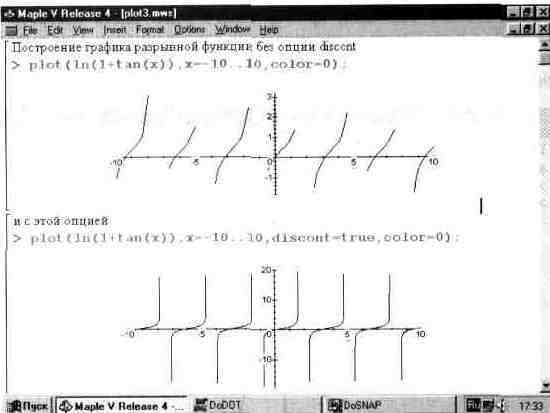
Рис. 13.3. Построение графиков функции с разрывами.
Обычно графики разных функций автоматически строятся разными цветами. Но они не всегда удовлетворяют пользователя — например, при распечатке графиков монохромным принтером некоторые кривые могут выглядеть слишком блеклыми или даже не пропечататься вообще. Используя списки параметров color (цвет линии) и style (стиль линий) можно добиться выразительного выделения кривых — это показывает второй пример на рис. 13.4.
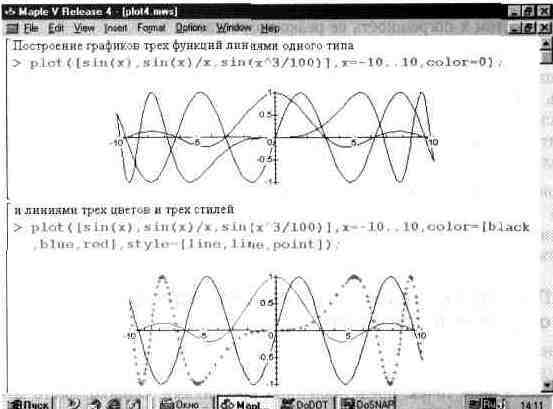
Рис. 13.4. Графики трех функции на одном рисунке.
На рис. 13.5 показан еще один пример такого рода. Здесь построен график функции sin(x)/x и график ее полиномиальной аппроксимации. Она выполняется настолько просто, что соответствующие функции записаны прямо в списке параметров функции plot.
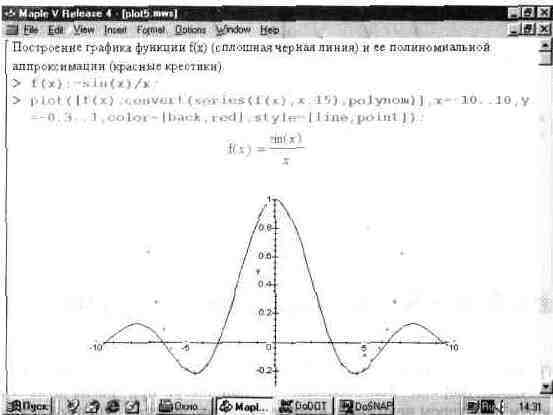
Рис. 13.5. График функции sin(x)/x и ее полиномиальной аппроксимации.
В данном случае сама функция построена сплошной линией, а график полинома — крестиками. Хорошо видно, что при малых х аппроксимация дает высокую точность, но затем с ростом х погрешность ее резко возрастает.
Рис. 13.6 показывает построение нескольких любопытных функций, полученных с помощью комбинаций элементарных функций. Эти комбинации позволяют получать периодические функции, моделирующие сигналы стандартного вида в технических устройствах: в виде напряжения на выходе двухполупериодного выпрямителя, симметричных прямоугольных колебаний (меандр), пилообразных и треугольных импульсов, треугольных импульсов со скругленной вершиной.
В этом рисунке запись axes=NONE убирает координатные оси. Обратите внимание, что смещение графиков отдельных функций вниз с целью устранения их наложения достигнуто просто прибавлением к записи каждой функции некоторой константы.
13.2.6. Построение графиков функций, заданных отдельными точками
Показанный на рис. 13.5 график полинома, построенный крестиками, не означает, что полином представлен отдельными точками. В данном случае просто выбран стиль линии в виде точек, представленных крестиками. Однако, часто возникает необходимость построения графиков функции, которые представлены просто совокупностью точек. Она может быть создана искусственно, как на рис. 13.7, либо просто задаваться списком координат х и значений функции.
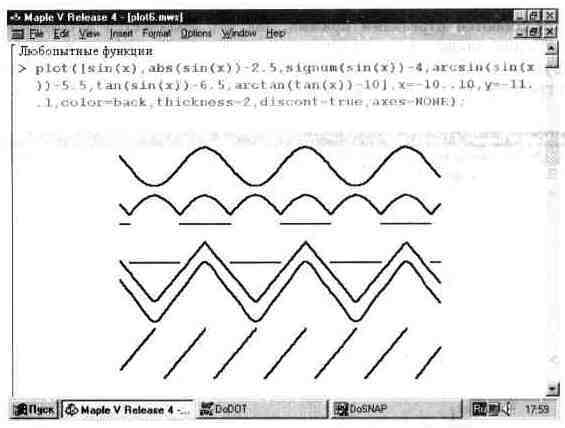
Рис. 13.6. Построение графиков нескольких любопытных функции.
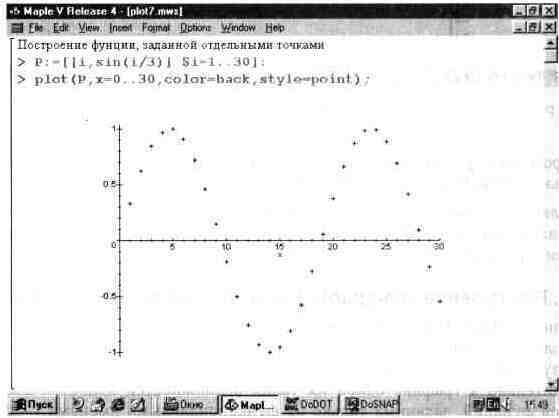
Рис. 137. Формирование списка отдельных точек функции и их построение на графике.
В данном случае переменная Р имеет вид списка, в котором попарно перечислены координаты точек функции sin(x). В этом нетрудно убедиться, заменив знак «:» после выражения, задающего Р на знак «;». Далее по списку Р построен график точек в виде крестиков, которые отображают отдельные значения функции sin(x).
На рис. 13.8 показано построение графиков функций по точкам при явном задании функции списком координат ее отдельных точек. В первом примере эти
точки соединяются отрезками прямых, так что получается кусочно-линейный график. Видно также, что указание типа точек после указания стиля линии игнорируется, — а жаль, было бы неплохо, чтобы наряду с кусочно-линейной линией графика строились и выделенные окружностью точки.
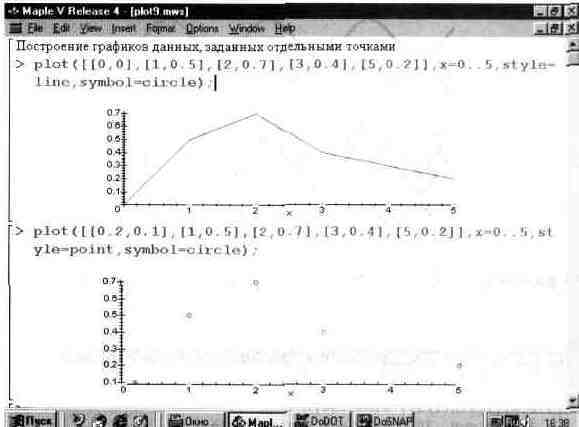
Рис. 13.8. Построение графика функции явно заданной отдельными точками.
Во втором примере рис. 13.8 показано построение только точек заданной функциональной зависимости. Они представлены маленькими кружками.
Читателю предлагается совместить самому оба подхода к построению графиков по точкам и создать график в виде отрезков прямых, соединяющих заданные точки функции, представленные кружками или крестиками.
13.2.7. Построение графиков функций, заданных их именами
Способность Maple V к упрощению работы пользователя просто поразительна — жаль только, что многие возможности этого становятся ясными после основательного изучения системы, на что уходят увы не дни, а месяцы, а то и годы. Применительно к графике одной их таких возможностей является построение графиков функций, заданных только их функциональными именами — даже без указания параметров в круглых скобках. Такую возможность наглядно демонстрирует рис. 13.9.
Этот пример показывает, что возможно построение графиков функций даже без применения в команде plot указателей масштабов. При этом масштаб по горизонтальной оси устанавливается равным по умолчанию -10..10, а по вертикальной оси устанавливается автоматически в соответствии с экстремальными значениями функций в указанном диапазоне изменения независимой переменной — условно х.
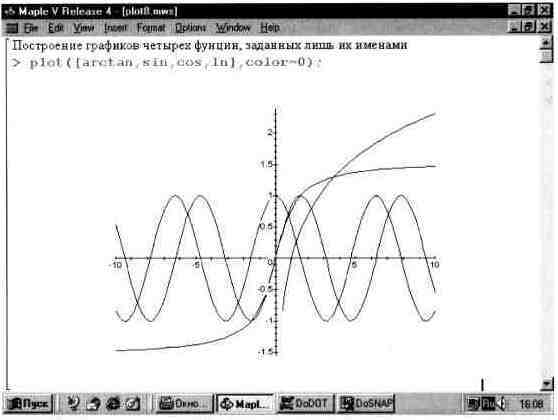
Рис. 13.9. Построение графиков четырех функции, заданных только их именами.
13.2.8. Построение графиков функции с ординатами, заданными вектором
Часто возникает необходимость построения графика точек, ординаты которых являются элементами некоторого вектора. Обычно при этом предполагается равномерное расположение точек по горизонтальной оси.
Пример построения такого графика дан на рис. 13.10.
Из этого примера нетрудно заметить, что данная задача решается составлением списка парных значений координат исходных точек — к значениям ординат точек, взятых из вектора добавляются значения абсцисс. Они задаются чисто условно, поскольку никакой информации об абсциссах точек в исходном векторе нет. Так что фактически строится график зависимости ординат точек от их порядкового номера п.
13.2.9. Построение графиков функций, заданных процедурами
Некоторые виды функций, например кусочные, удобно задавать процедурами. Построение графиков функций, заданных процедурами, не вызывает никаких трудностей и иллюстрируется рис. 13.11.
Здесь, пожалуй, полезно обратить внимание на то, что когда в функции plot указывается имя процедуры без списка ее параметров, то указатель масштаба должен просто указывать пределы графических построений по оси х.
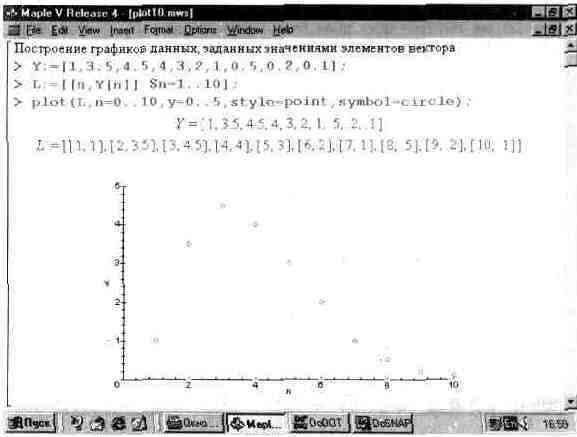
Рис. 13.10. Построение графика точек с ординатами, заданными элементами вектора.
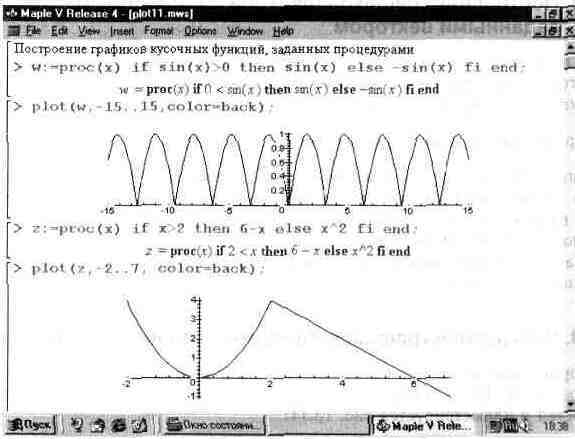
Рис. 13.11. Построение графика функций, заданных процедурами
13.2.10. Построение графиков функций, заданных функциональными операторами
Еще одна «экзотическая» возможность функции plot — построение графиков функций, заданных функциональными операторами. Она иллюстрируется рис. 13.12.
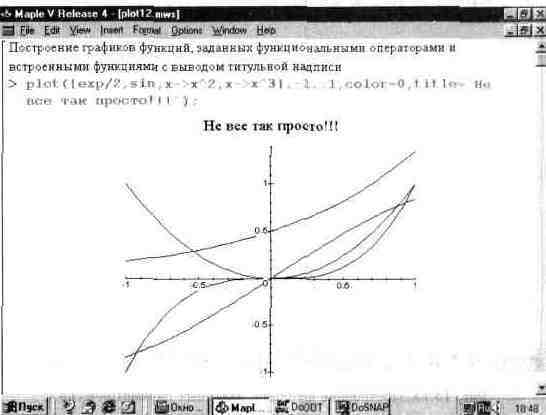
Рис. 13.12. Построение графиков функции, заданной функциональными операторами.
Имена функции (без указания списка параметров в круглых скобках тоже по существу являются функциональными операторами. Так что и они могут использоваться при построении графиков упрощенными способами.
13.2.11. Построение графиков функций, заданных параметрически
В ряде случаев для задания некоторых зависимостей используются заданные параметрически уравнения, например x=fl(t) и y=f2(t) при изменении переменной t в некоторых пределах. Точки (х,у) наносятся на график в Декартовой системе координат и соединяются отрезками прямых. Для этого используется функция plot в следующей форме:
plot([fl(t),f2(t),t=tmin..tmax],h,v,p)
Если функции fl(t) и f2(t) содержат периодические функции (например, тригонометрические), то для получения замкнутых фигур диапазон изменения переменной t задается обычно 0..2*Pi или -Pi..Pi. К примеру, если задать в качестве функций fl(t) и f2(t) функции sin(t) и cos(t), то будет получен график окружности. Рис. 13.!3 показывает другие, чуть менее тривиальные примеры построения графиков такого рода.
Задание указателей масштаба h и v, а также параметров р не обязательно. Но, как и ранее, позволяет получить вид графика, удовлетворяющий всем требования пользователя.
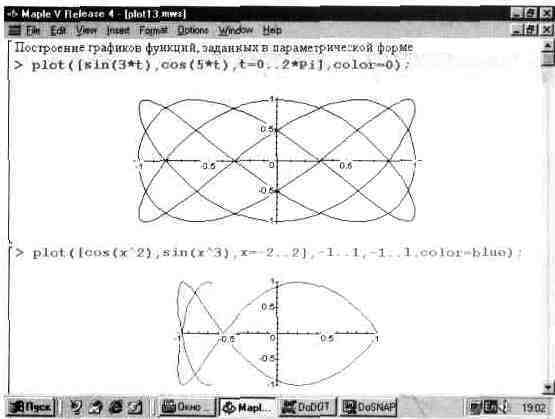
Рис. 13.13. Построение функции, заданных параметрически.
13.2.12. Построение графиков функций в полярной системе координат
Графики в полярной системе координат представляют собой линии, которые описывает конец радиус вектора r(t) при изменении угла t в определенных пределах — от tmin до tmax. Построение таких графиков производится также функцией plot, которая записывается в следующем виде:
plot([r(t),theta(t),t=tmin..tmax],h,v,p,coords=polar)
Здесь существенным моментом является задание полярной системы координат опцией coords=polar. Рис. 13.14 дает примеры построения графиков функций в полярной системе координат.
Графики параметрических функций и функций в полярной системе координат отличаются огромным разнообразием. Снежинки и узоры мороза на стеклах, некоторые виды кристаллов и многие иные физические объекты подчиняются математическим закономерностям, положенным в основу построения таких графиков.
13.3. Построение ЗО-графиков с помощью функция plot3d
13.3.1. Особенности применения функции plot3d
Для построения графиков трехмерных поверхностей Maple имеет встроенную в ядро функцию plot3d. Она может использоваться в следующих форматах:
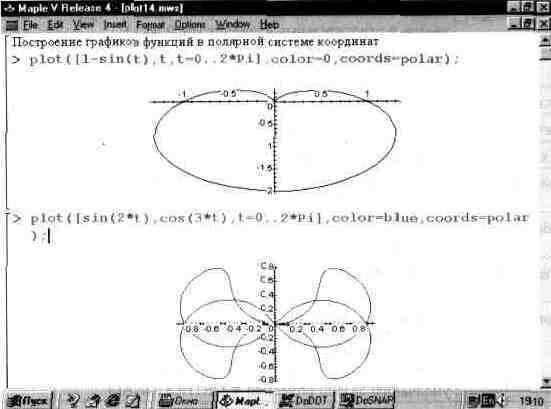
Рис. 13.14. Построение графиков функций в полярной системе координат.
plot3d(exprl, x=a..b, y=c..d,p) plot3d(f, a..b, c..d,p)
plot3d([exprf,exprg,exprh], s=a..b, t=c..d,p) plot3d([f,g,h], a..b, c..d,p).
В двух первых формах plot3d применяется для построения обычного графика одной поверхности, в других формах — для построения графика с параметрической формой задания поверхности. В приведенных формах: f, g и h — функции, expri — выражение, отражающее зависимость от х и у, exprf, exprg и exprh — выражения, задающие поверхность параметрически, s, t, а и b — числовые константы действительного типа, end — числовые константы или выражения действительного типа, х, у, s и t — имена независимых переменных и р — параметры-опции. Параметры для функции plot3d задаются аналогично их заданию для функции plot.
13.3.2. Параметры функции plot3d
С помощью параметров р можно в широких пределах управлять видом трехмерных графиков, выводя или убирая линии каркасной сетки, вводя функциональную окраску поверхностей, меняя угол их обзора и параметры освещения, изменяя вид координатных осей и т.д.
Следующие параметры функции plot3d задаются аналогично их заданию для функции plot:
axesfont font color coords font labelfont linestyle numpoints scaling style symbol thickness title titlefont
Однако функция plot3d имеет ряд дополнительных специфических параметров:
| ambientlight=[r,g,o] | Задает интенсивность красного (red), зеленого (green) и синего (blue) цветов в относительных единицах (от 0 до 1). |
| axes=f | Задает вид координатных осей (BOXED, NORMAL, FRAME и NONE, по умолчанию NONE). |
| grid=[m,nl | Задает число линии каркаса поверхности. |
| gridstyle=x | Задает стиль линий каркаса х ( 'rectangular' или 'triangular'). |
| labels=[x,y,z] | Задает надписи по осям (х, у и z — строки, по умолчанию пустые). |
| light=[phi,theta,r,g, b] | Задает углы, под которыми расположен источник освещения поверхности и интенсивности составляющих (г, g и b) цвета. |
| lightmodel=x | Задает режим яркости (соответственно, none", 'lightl', 'light2', 'light3' и 'light4'). |
| orientation=[theta, phi] | Задает углы ориентации поверхности (по умолчанию 45 градусов). |
| projection=r | Задает перспективу при обзоре поверхности (г может быть числом 0 или 1, задающим включение или выключение перспективы, а также одной из строк 'FISHEYE', 'NORMAL', или 'ORTHOGONAL' (это соответствует численному значению г 0, 0.5, или 1, соответственно, причем по умолчанию задано projection = ORTHOGONAL). |
| shading=s | Задает направления, по которым меняется цвет функциональной окраски (значения s могут быть XYZ, XY, Z, ZGREYSCALE, ZHUE, NONE). |
| tickmarks=[l,n,m] | Задает характер маркировки по осям х, у и z (числа 1, п и m имеют значения не менее 1). |
| view=zmin..zmax или Ixmin..xmax,ymin.. ymax,zmin..zmax] | Задает минимальные и максимальные координаты поверхности для ее видимых участков. |
13.3.3. Выбор и пересчет координат ЗО-графиков
Для трехмерных графиков возможно задание 31-го типа координатных систем с помощью параметра соога5=Тип_координатнои_системь1. Поскольку на экране дисплея поверхность отображается только в прямоугольной системе координат и характеризуется координатами х, у и z, то для представления поверхности, заданной в иной системе координат с координатами u, v и w используются известные [46,47] формулы для преобразования (u, v, w) --> (х, у, z). Ниже представлены типы координатных систем для трехмерной графики и соответствующие формулы преобразования:
bipolarcylindrical
х = a*sinh(v)/(cosh(v)-cos(u)) у = a*sin(u)/(cosh(v)-cos(u)) z = w
bispherical
х = sin(u)*cos(w)/d у = sin(u)*sin(w)/d z = sinh(v)/d (где d = cosh(v) - cos(u) )
cardiodal
x = u*v*cos(w)/(lГ2+v»2)-2 у = u*v*sin(w)/(ir2+v"2r2 z = (u"2-v'2)/2/^2+v'2)-2
cardiodcylindrical
x = (u'2-v~2)/2/(u'-2+v~2)'-2 у = u*v/(u'2+v-2)"2 z = w
casscylindrical
x = a*2~(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+l)-(l/2)+exp(u)*cos(v)+l)-(l/2) y= a*2«(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+l)"(l/2)-exp(u)*cos(v)-l)"(l/2) z = w
confocalellip
x = ((a~2-u)*{a'2-v)*(a"2-w)/{a'2-b''2)/(a-2-c-2)Y(l/2) у = ((b»2-u)*(b~2-v)*(b"2-w)/(b"2-a»2)/(b»2-c«2))'(l/2) z = ((c''2-u)*(^2-v)*(c''2-w)/(c'2-a'2)/(c^2-\)''2))~(l/2)
confocalparab
x = ((a'2-u)*(si'2-v)*(a'2-w)/{V2-a'2))'(l/2) у = ((b»2-u)*(b»2-v)*(b-2-w)/(b-2-a-2) Г(1/2) z = (a"2+b"2-u-v-w)/2
conical
x = u*v*w/(a*b) у = u/b*((v"2 - h~2)*(b~2-w''2)/(a~2-V2)Y(l/2) z = u/a*((a'2 - v'2)*(a'2 - w~2)/(a-2-b»2))"(l/2)
cylindrical
x = u*cos(y) у = u*sin(y) z = w
ellcylindrical
x = a*cosh(u)*cos(v) у = a*sinh(u)*sin(v) z = w
ellipsoidal
x = u*v*w/a/b у = ((u'^-b^Mv^-b^^b^-w^Aa^-b^^l^/b z = ((u-2-a»2)*(a•2-v«2)*(a»2-w"2)/(a•2-b'2))»(l/2)/a
hypercylindrical
x= ((u"2+v"2Y(l/2)+u)'(l/2) y^u^+v^ni^-iO-O/^) z=w
invcasscylindrical
x = a*2-(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+l)-(l/2) +
exp(u)*cos(v)+l)'(l/2)/(exp(2*u)+2*exp(u)*cos(v)+l)'(l/2) у = a*2-(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+l)-(l/2) -
exp(u)*cos(v)-l)»(l/2)/(exp(2*u)+2*exp(u)*cos(v)+l)«(l/2) z = w
invellcylindrical
x = a*cosh(u)*cos(v)/(cosh(ur2-sin(v)"2) у = a*sinh(u)*sin(v)/(cosh(u)"2-sin(v)~2) z = w
invoblspheroidal
x = a*cosh(u)*sin(v)*cos(w)/(cosh(u)"2-cos(v)«2) у = a*cosh(u)*sin(v)*sin(w)/(cosh(u)'2-cos(v)"2) z = a*sinh(u)*cos(v)/(cosh(u)«2-cos(v)'2)
invprospheroidal
x = a*sinh(u)*sin(v)*cos(w)/(cosh(u)'2-sin(v)"2) у = a*sinh(u)*sin(v)*sin(w)/(cosh(u)«2-sin(v)«2) z = a*cosh(Ll)*cos(v)/(cosh(u)»2-s^n(v)•2)
logcoshcylindrical
x = !i/Pi*\n(cosh(uY2-sm(vY2} у = 2*a/Pi*arctan(tanh(u)*tan(v)) z = w
maxwellcylindrical
x = a/Pi*(u+l+exp(u)*cos(v)) у = a/Pi*(v+exp(u)*sin(v)) z = w
oblatespheroidal
x = a*cosh(u)*sin(v)*cos(w) у = a*cosh(u)*sin(v)*sin(w) z = a*sinh(u)*cos(v)
paraboloidal
x = u*v*cos(w) у = u*v*sin(w) z = (u"2 - v'2)/2
paraboloidal2
x = 2*((u-a)*(a-v)*(a-w)/(a-b))-(l/2) у = 2*((u-b)*(b-v)*(b-w)/(a-b))-(l/2) z = u+v+w—a—b
paracylindrical
x = (u'2 - v'2)/2 у = u*v z = w
prolatespheroidal
x = a*sinh(u)*sin(v)*cos(w) y=a*sinh(u)*sin(v)*sin(w) z=a*cosh(u)*cos(v)
rectangular
x = и у = v • z = w
rosecylindrical
x = ((1Г2+у-2)-(1/2)+и)-(1/2)/(1Г2+у-2Г(1/2) у = ((u'2+v'2y(l/2)-uY(l/2)/(u'2+v'2V(\/2) z = w
sixsphere
x= u/(u'2+v'2+w'2) у = v/(u'-2+v'2+v/''2) z = w/(u'2+v'2+w'2)
spherical
x = u*cos(v)*sin(w) у = u*sin(v)*sin(w) z = u*cos(w)
tangentcylindrical
x = u/(ir2+v"2) у = v/(u«2+v»2) z = w
tangentsphere
x = u-costwVdj^+v^) у = u*sin(w)/(ir2+v"2) z = v/(u"2+v~2)
toroidal
x = a*sinh(v)*cos(w)/d у = a*sinh(v)*sin(w)/d z = a*sin(u)/d (где d = cosh(v) - cos(u) )
Эти формулы полезно знать, поскольку в литературе встречаются несколько отличные формулы пересчета.
Вид графиков трехмерных поверхностей очень сильно различается в разных
координатных системах. По умолчанию трехмерные графики строятся в прямоугольной системе координат — rectangular.
13.4. Примеры построения трехмерных поверхностей с помощью функции plot3d
13.4.1. Простейшее построение ЗО-поверхности с разным стилем
На рис. 13.15 показано два примера простейших построений графиков трехмерной поверхности. По умолчанию строится каркасная поверхность с функциональной окраской тонких линий каркаса и удалением невидимых линий. Чтобы график выглядел более четким, построение в первом примере задано линиями черного цвета с помощью параметра color-black.
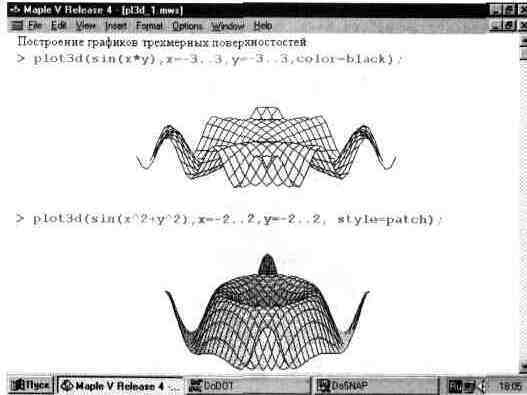
Рис. 13.15. Примеры простейшего построения трехмерных поверхностей.
Во втором примере та же поверхность построена с параметром style=patch, что приводит к появлению ее функциональной окраски (увы, на рисунках в книге воспринимаемой как окраска оттенками серого цвета). Функциональная окраска делает рисунки более информативными.
Помимо значения path, можно задавать ряд других стилей для построения трехмерных поверхностей: point — точками, contour — контурными линиями, line — линиями, hidden — линиями каркаса с удалением невидимых линий, wireframe — линиями каркаса со всеми видимыми линиями, patchnogrid — с раскраской, но без линий каркаса, patchcontour — раскраска с линиями равного уровня.
Цвет трехмерного графика может задаваться (как и у двумерного) опцией со1ог=с, где с — цвет (оттенки цвета указывались выше). Возможно еще два алгоритма задания цвета:
HUE — алгоритм с заданием цвета в виде color=f(x,y);
RGB — алгоритм с заданием цвета в виде color=[exprr,exprg,exprb], где выражения exprr, exprg и exprb — выражения, задающие относительную значимость (от О до 1) основных цветов (красного — red, зеленого — green и синего — blue).
Удачный выбор углов обзора фигуры и применение функциональной окраски позволяют придать построениям трехмерных фигур весьма эффектный и реалистический вид.
13.4.2. Построение фигур в различных системах координат
Как отмечалось, вид графика трехмерной поверхности существенно зависит от выбора координатной системы. Рис. 13.16 показывает пример построения нелинейного конуса в цилиндрической системе координат. Для задания такой системы координат используется параметр coords=cylindrical.
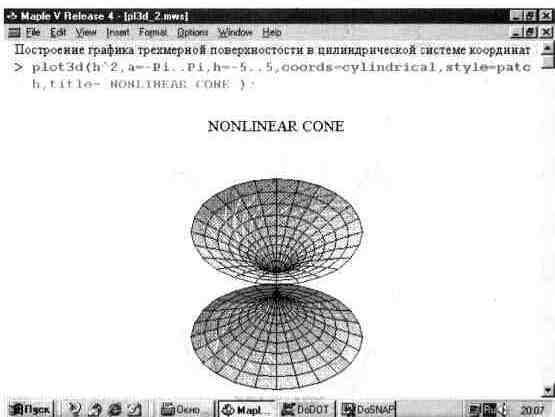
Рис. 13.16. Нелинейная цилиндрическая поверхность.
При построении этой фигуры также использована цветная функциональная окраска. Кроме того, этот пример иллюстрирует вывод над рисунком титульной надписи.
Приведем еще один пример построения трехмерной поверхности — на этот раз в сферической системе координат (рис. 13.17). Здесь функция задана вообще элементарно просто — в виде числа 1. Но поскольку выбрана сферическая система координат, то строится поверхность шара единичного радиуса.
При этом построении также задана функциональная окраска поверхности и вывод титульной надписи.
О том, насколько необычным может быть график той или иной функции в различных системах координат свидетельствует рис. 13.18. На нем показан график параметрически заданной функции от одной координаты t — sin(t"3), построенный в сферической системе координат.
Кстати, рис. 13.18 иллюстрирует возможность одновременного наблюдения более чем одного окна — в данном случае двух окон. В одном окне задано построение графика, а в другом — построен сам график. При построении графика в отдельном
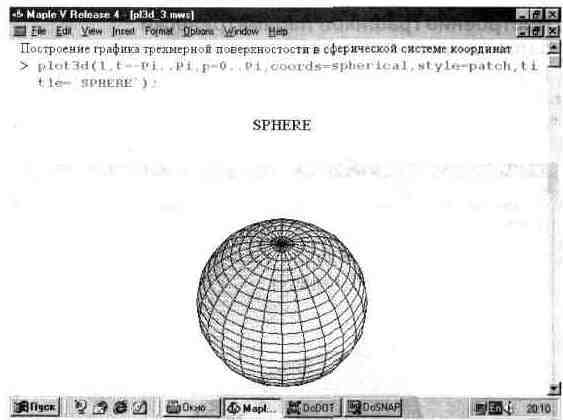
Рис. 13.17. Построение шарообразной поверхности в сферической системе координат.
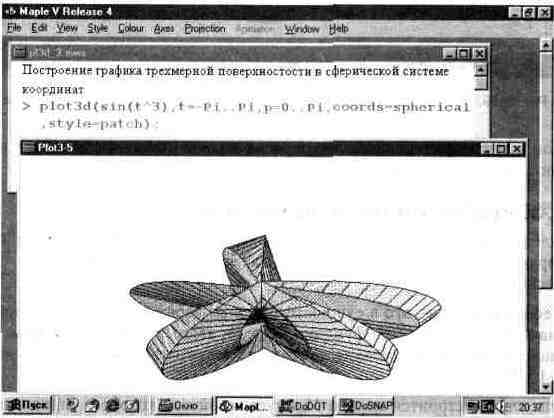
Рис. 13.18. График еще одной поверхности в сферической системе координат.
окне появляется панель форматирования графика. С помощью ее довольно наглядных кнопок-пиктограмм можно легко скорректировать вспомогательные параметры графика (окраску, наличие линий каркаса, ориентацию и др.).
13.4.3. Построение графиков параметрически заданных поверхностей
На рис. 13.19 показано построение поверхности при полном ее параметрическом задании. В этом случае поверхность задается тремя формулами, содержащимися в списке.
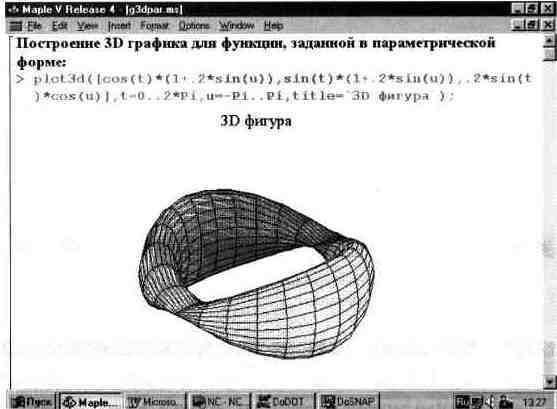
Рис. 3.19. График ЗО-поверхности при полном параметрическом ее задании.
В данном случае функциональная окраска задана из меню, поэтому в состав функции соответствующий параметр не введен.
13.4.4. ЗО-график как графический объект
Принадлежность функции plot и plot3D к функциям (в ряде книг их именуют операторами, командами или процедурами) наглядно выявляется при создании графических объектов.
Графический объект — это в сущности обычная переменная, которой присваивается значение графической функции. После этого такая переменная, будучи вызванной, вызывает построение соответствующего графика. Пример этого дан на рис. 13.20.
В данном случае строится кольцо Мебиуса, свойства которого (например, плавный переход с одной стороны ленты на другую) уже много веков будоражат воображение людей.
13.4.5. Задание 30-графики в виде процедуры
Язык программирования Maple V допускает применение в процедурах любых внутренних функций, в том числе графических. Пример такого применения дает рис. 13.21.
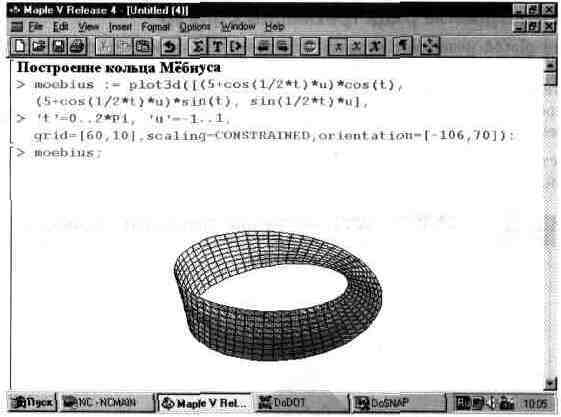
Рис. 13.20. Пример задания и вывода трехмерного графического объекта
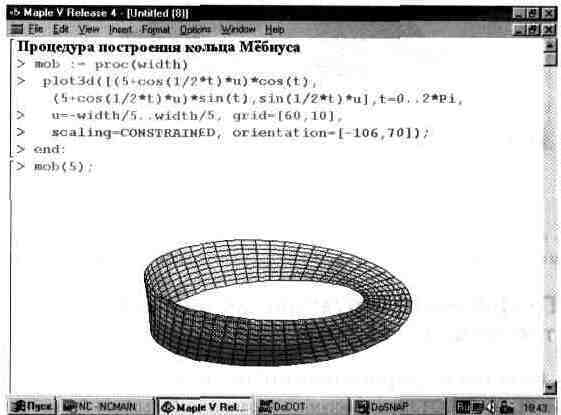
Рис. 13.21. Пример создания и применения процедуры ЗО-графики.
Этот пример показывает еще один способ задания и построения кольца Мебиуса. Практически любые графические построения можно оформлять в виде процедуры и использовать такие процедуры в своих документах. Подробно создание графических процедур описано в книге [38], поставляемой в составе коммерческой реализации системы.
13.4.6. Построение ряда трехмерных фигур
Функция plot3d позволяет строить одновременно несколько фигур, пересекающихся в пространстве. При этом она обладает уникальной возможностью — автоматически вычисляет точки пересечения фигур и показывает только видимые части соответствующих фигур. Это создает графики фигур, выглядящие вполне естественно.
Для построения таких графиков достаточно вместо одной функции указать ряд функций. Пример такого построения для двух функций показан на рис. 13.22.
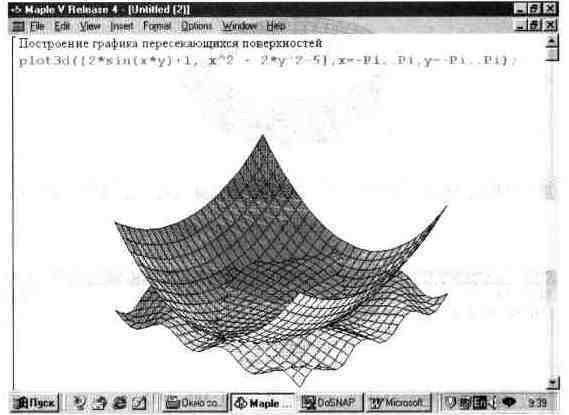
Рис. 13.22. Пример построения двух SD-фигур, пересекающихся в пространстве.
Фигура на рис. 13.22 показана после ее коррекции и функциональной окраски в «ручном» режиме — с применением инструментальной панели окна графики.
13.5. Графические структуры двумерной и трехмерной графики
13.5.1. Понятие о графических структурах
Функции PLOT и PLOT3D, с именами, набранными большими буквами, позволяют создавать графические структуры, содержащие ряд графических объектов si, s2, s3 и т.д. Каждый объект может представлять собой точку или фигуру, полигон, надпись и т.д., позиционированную с высокой точностью в заданной системе координат. Координатные оси также относятся к графическим объектам. Важно отметить, что функции PLOT и PLOT3D одновременно являются данными, описывающими графики. Их можно записывать в виде файлов и (после считывания файлов) представлять в виде графиков. Особые свойства этих функций подчеркиваются записью их прописными буквами.
13.5.2. Графические структуры двумерной графики
Графическая структура двумерной графики задается в виде:
PLOT(sl, s2, s3,...,o);
где si, s2, s3 .... — графические объекты (или элементарные структуры-примитивы), о — общие для структуры опции).
Основными объектами являются:
POINTS([xl,yl],[x2,y2),...[xn,ynj) — построение точек, заданных их координатами;
CURVES([[xll,yll],...[xln,yln]],[[x21,y21],...[x2n,y2n]],...[[xml,yml]„.. [xmn,yrnn]]) — построение кривых по точкам;
POLYGONS([[xll,yll¦,...[xln,yln]],[[x21,y2H,...[x2n,y2n]],...[[xml,yml],... [xmn.ymn]]) — построение замкнутой области — полигона (последняя точка должна совпадать с первой);
ТЕХТ([х, у], 'string', horizontal, vertical) — вывод текстовой надписи 'string', позиционированной координатами [х,у] с горизонтальной или вертикальной ориентацией. Опция horizontal может иметь значения ALIGNLEFT или ALIGNRIGHT, указывающие, в какую сторону (влево или вправо) идет надпись. Аналогично опция vertical может иметь значения ALIGNABOVE или ALIGNBELOW, указывающие, в каком направлении (вверх или вниз) идет надпись.
При задании графических объектов (структур) si, s2, s3 и т.д. можно использовать описанные выше опции и параметры, например, для задания стиля STYLE-построения (POINT, LINE, PATCH, PATCHNOGRID), толщины линий THICKNESS (кроме координатных осей), символа SYMBOL, которым строятся точки кривых (BOX, CROSS, CIRCLE, POINT, DIAMOND и DEFAULT), стиля линий LINESTYLE, цвета COLOUR (например, COLOUR(HUE.O) для закраски непрерывной области), типа шрифта FONT, вывода титульной надписи TITLE(string), имени объекта NAME(string), стиля координатных осей AXESSTY-LE (BOX, FRAME, NORMAL, NONE, или DEFAULT) и т.д.
Следует отметить, что опции в графических структурах задаются несколько иначе — с помощью круглых скобок. Например, для задания фонта TIMES ROMAN с размером символов 16 надо записать FONT(TIMES, ROMAN, 16), а для задания стиля координатных осей в виде ящика (прямоугольника) — AXESSTYLE(BOX) и т.д.
На рис. 13.23 показан пример графических построений при использовании основных структур двумерной графики.
Как видно из этого примера, графическая двумерная структура позволяет задать практически любые двумерные графики и текстовые надписи в пределах одного рисунка.
13.5.3. Графические структуры трехмерной графики
Графические структуры трехмерной графики строятся на основе функции plot3d:
PLOT3D(sl, s2,s3,....,o)
В качестве элементарных графических структур можно использовать уже описанные выше объекты POINTS, CURVES, POLYGONS и TEXT — разумеется, с
добавлением в списки координат третьей координаты. Пример такого построения дан на рис. 13.24.
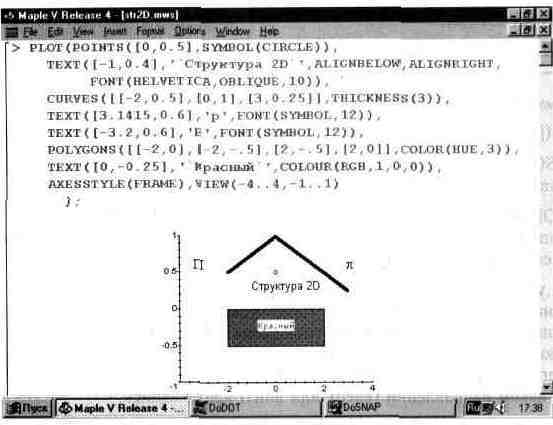
Рис. 13.23. Пример использования структур 20-графики
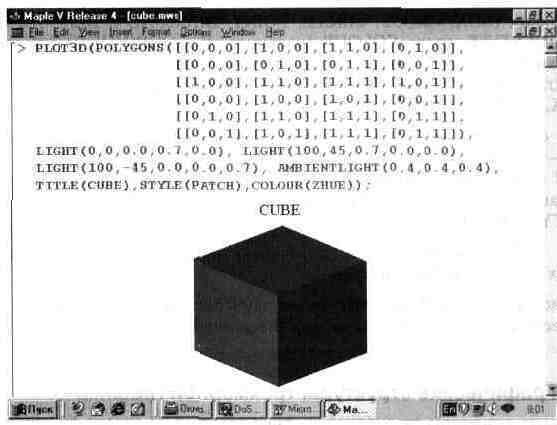
Рис. 13.24. Пример создания ЗО-структуры.
Кроме того, могут использоваться следующие специальные трехмерные структуры. Одна из них — структура:
GRID(a..b,c..d,listlist) — задание поверхности над участком координатной плоскости [a,b]([c,d] по данным заданным списочной переменной listlist:= [[zll,...zln],[z21,...z2n],...[zml...zmn]] с размерностью nxm. Заметим, что эта переменная задает координату z для равноотстоящих точек поверхности.
На рис. 13.25 показан пример создания трехмерной графической структуры на базе GRID. Изображение представляет собой линии, соединяющие заданные точки.
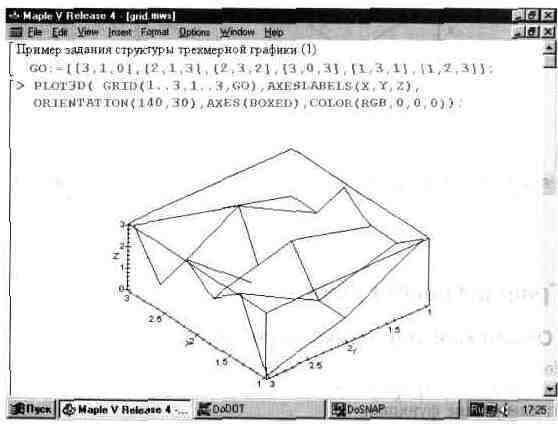
Рис. 13.25. Пример задания графической структуры типа GRID.
Еще один тип трехмерной графической структуры это:
MESH(listlist) — задание трехмерной поверхности по данным списочной переменной listlist, содержащей полные координаты всех точек поверхности (задание последней возможно при неравномерной сетке).
Обычная форма задания этой структуры следующая:
MESH([[[xll,yll,zll],...[xln,yln,zln]], [[x21,y21,z21],...[x2n,y2n,z2n]], ... [[xml,yml,zml]...[xmn,ymn,zmn]]]).
Пример задания такой структуры представлен на рис. 13.26.
Описанные структуры могут использоваться и в программных модулях. Много примеров их описано в книге [38].
Дополнительные данные о возможностях графических структур можно найти в справочной базе данных системы Maple V.
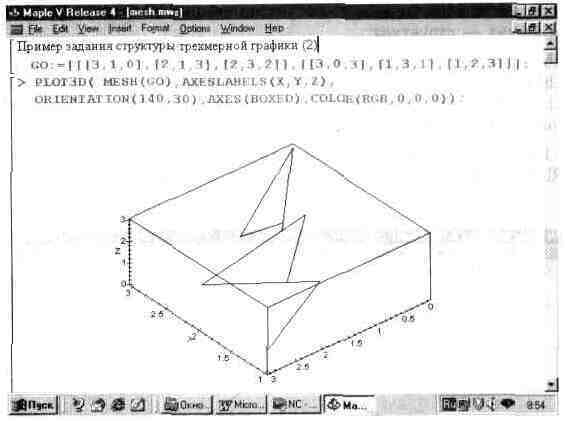
Рис. 13.26. Пример задания графической структуры типа MESH.
13.6. Графика пакета plots 13.6.1. Общая характеристика пакета plots
Пакет plots содержит почти полсотни графических функции, существенно расширяющих возможности графики системы Maple V. В реализации R4 этот пакет содержит следующие функции:
| ——————————— animate | Создает мультипликацию 2D графиков функций. |
| animated | Создает мультипликацию 3D графиков функции. |
| changecoords | Смена системы координат. |
| compiexplot | Построение 20-графика на комплексной плоскости. |
| complexplot3d | Построение 30-графика в комплексном пространстве. |
| conformal | Конформный график комплексной функции. |
| contourplot | Строит координатную систему контурши-м графика. |
| contourplot3d | Строит контурный 30-график. |
| coordplot | Строит координатную систему 20-графиков. |
| coordplotSd | Строит координатную систему ЗО-графиков. |
| cylinderplot | Строит график 3D поверхности в цилиндрических координатах. |
| densityplot | Строит двумерный график плотности. |
| display | Строит график списка графических объектов. |
| display3d | Строит график списка трехмерных графических объектов. |
| fieldplot | Строит график 2D векторного поля. |
| fieldplot3d | Строит график 3D векторного поля. |
| gradplot | Строит график 2D векторного поля градиента. |
| gradplot3d | Строит график 3D векторного поля градиента. |
| implicitplot | Строит 2D-гpaфик неявной функции. |
| implicitplot3d | Строит ЗО-график неявной функции. |
| inequal | Строит график решения системы неравенств. |
| listcontplot | Строит 20-контурный график для сетки значении. |
| listcontplot3d | Строит ЗО-контурныи график для сетки значении. |
| listdensityplot | Строит 20-график плотности для сетки значении. |
| listplot | Строит 20-график для листа значений. |
| listplot3d | Строит ЗО-график для листа значении. |
| loglogplot | Строит логарифмический 20-график функции. |
| logplot | Строит полулогарифмический 2D- график функции. |
| matrixplot | Строит ЗО-график со значениями Z, определенными матрицей. |
| odeplot | Строит 2D или 3D график решения дифференциальных уравнений. |
| pareto | Строит pareto-диаграммы (гистограмма + график линиями). |
| pointplot | Строит 2D точечный график. |
| pointplot3d | Строит 3D точечный график. |
| polarplot | Строит график 2D кривой в полярной системе координат. |
| polygonplot | Строит график одного или большего количества многоугольников. |
| polygonplot3d | Строит график одного или большего количества многоугольников. |
| polyhedraplot | Строит трехмерный график многогранника. |
| replot | Перестраивает заново график. |
| rootlocus | Строит график корней уравнения с комплексными неизвестными. |
| semilogplot | Строит график функции с логарифмическим масштабом по горизонтали. |
| setoptions | Устанавливает опции по умолчанию для 2D графиков. |
| setoptions3d | Устанавливает опции по умолчанию для 3D графиков. |
| spacecurve | Строит 3D пространственные кривые. |
| sparsematrixplot | Строит ZD-график отличных от нуля значений матрицы. |
| sphereplot | График 3D- поверхности в сферических координатах. |
| surfdata | Строит ЗD-гpaфик поверхности по численным данным. |
| textplot | Выводит на заданное место 2D-гpaфикa текст. |
| textplot3d | Выводит на заданное место ЗD-rpaфикa текст. |
| tubeplot | Строит ЗD-rpaфики типа трубы. |
Среди этих функций надо отметить прежде всего средства построения графиков ряда новых типов (например, в виде линий равного уровня, векторных полей и т.д.), а также средства объединения различных графиков в один. Особый интерес представляют две первые функции, обеспечивающие оживление (анимацию) как двумерных графиков (animate), так и трехмерных (animate3d). Этот пакет вполне
заслуживает описания в отдельной книге. Но, учитывая ограниченный объем данной книги, мы рассмотрим лишь несколько характерных примеров его применения. Заметим, что для использования приведенных функций нужен вызов пакета, например, командой with(plots).
13.6.2. Построение графиков функций в двумерной полярной системе координат
В пакете plots есть функция для построения графиков в полярной системе координат. Она имеет вид polarplot(L,o), где L — объекты для задания функции, график которой строится и о — необязательные опции. На рис. 13.27 представлен пример построения графика с помощью функции polarplot.
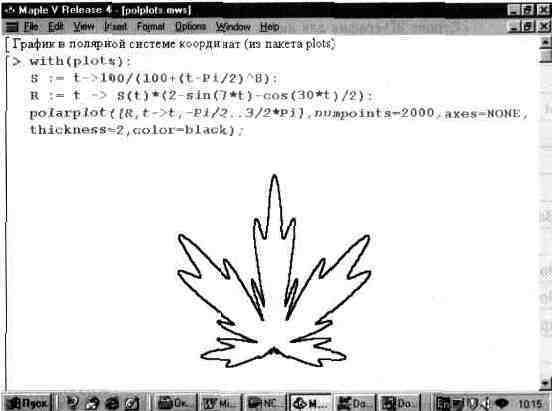
Рис. 13.27. График, построенный с помощью функции polarplot.
В данном случае для большей выразительности опущено построение координатных осей, а график выведен линией удвоенной толщины. График очень напоминает лист клена, весьма почитаемого в Канаде и ставшего эмблемой системы Maple V.
13.6.3. Построение графиков линиями равного уровня
Графики, построенные с помощью линий равного уровня (их также называют контурными графиками) часто используются в картографии. Эти графики получаются, если мысленно провести через трехмерную поверхность ряд равноотстоящих плоскостей, параллельных плоскости, образованной осями Х и Y графика. Линии равных высот образуются в результате пересечения этих плоскостей с трехмерной поверхностью.
Для построения таких графиков используется функция contourplot, которая может использоваться в нескольких форматах:
contourplot(exprl,x=a..b,y=c..d)
contourplot(f,a..b,c..d)
contourplot([ exprf,exprg,exprh ],s=a..b,t=c..d)
contourplot([ f,g,h ],a..b,c..d)
contourplot3d(exprl,x=a..b,y=c..d)
contourplot3d(f,a..b,c..d)
contourplot3d([ exprf,exprg,exprh ],s=a..b,t=c..d) »'
contourplot3d([ f,g,h ],a..b,c..d)
Здесь — f, g и h — функции, expri — выражение, описывающее зависимость высоты поверхности от координат х и у, exprf, exprg и exprh — выражения, зависящие от s и t, описывающие поверхность в параметрической форме, а и b — константы вещественного типа, end — константы или выражения вещественного типа, х, y,,s и t — имена независимых переменных.
На рис. 13.28 показано построение графика линиями равного уровня для одной функции. Опция filled=true обеспечивает автоматическую функциональную окраску замкнутых фигур, образованных линиями равного уровня. Порою это придает графику большую выразительность, чем при построении только линий равного уровня.
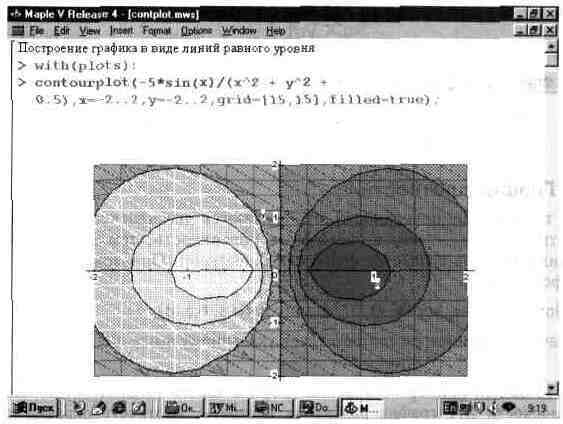
Рис. 13.28. Пример построения графика функции линиями равного уровня.
Функция contourplot позволяет строить и графики ряда функций. Пример такого построения показан на рис. 13.29. Множество окружностей на этом рисунке создается четырьмя поверхностями, заданными функциями с1, с2, сЗ и с4.
Следует отметить, что, хотя графики в виде линий равного уровня выглядят не так эстетично и естественно, как обычные графики трехмерных поверхностей (ибо требуют осмысления результатов), у них есть один существенный плюс — экстремумы функций на таких графиках выявляются порой более четко, чем на обычных графиках. Например, небольшая возвышенность или впадина за большой «горой» на обычном графике может оказаться невидимой, поскольку заслоняется
«горой» — на графике линий равного уровня этого эффекта нет. Однако выразительность таких графиков сильно зависит от числа линий равного уровня.
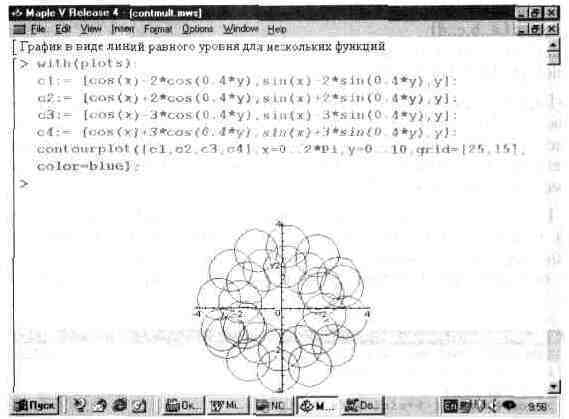
Рис. 13.29. Пример построения графиков многих функций линиями равного уровня.
13.6.4. График плотности
Иногда трехмерные поверхности отображаются на плоскости как графики плотности окраски — чем выше высота поверхности, тем плотнее окраска. Такой вид графиков создается функцией densityplot. Она может записываться в двух форматах:
densityplot(exprl,x=a..b,y=c..d) densityplot(f,a..b,c..d),
где назначение параметров соответствует указанному выше для функции contour-plot.
На рис. 13.30 дан пример построения графика такого типа. Нетрудно заметить, что в плоскости X,Y график разбит на квадраты, плотность окраски которых различна. В нашем случае плотность окраски задается оттенками серого цвета.
Обычно графики такого типа не очень выразительны, но имеют свои области применения. К примеру, оттенки окраски полупрозрачной жидкости могут указывать на рельеф поверхности дна емкости, в которой находится эта жидкость.
13.6.5. График векторного поля двумерный
Еще один распространенный способ представления трехмерных поверхностей — графики векторного поля. Они часто применяются для отображения полей, например, электрических зарядов. Особенность таких графиков в том, что для их построения используют стрелки, направление которых соответствует направлению изменения градиента поля, а длина — значению градиента.
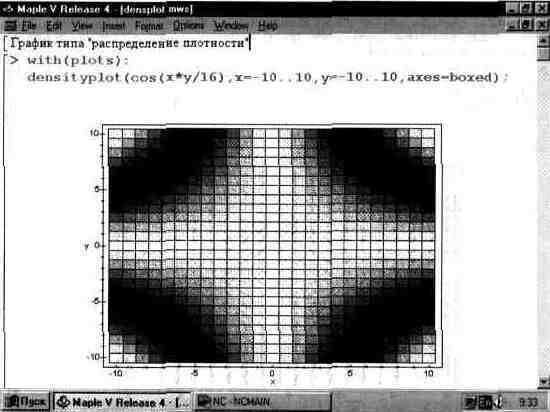
Рис. 13.30. График плотности для заданной функции.
Для построения таких графиков в двумерной системе координат используется функция fieldplot:
fieldplot(f, rl, r2) или fieldplot(f, rl, r2, ...),
где f — вектор или множество векторов, задающих построение, и rl и r2 — пределы.
На рис. 13.31 показан вид одного из таких графиков. Следует отметить, что для получения достаточного числа отчетливо видных стрелок надо поработать с форматированием графиков. Иначе графики этого типа могут оказаться не очень представительными. Так, слишком короткие стрелки превращаются в черточки и даже точки, не имеющие острия, что лишает графики наглядности.
Чуть позже мы рассмотрим построение на одном рисунке графиков плотности и векторного поля, а также создание более наглядных жирных стрелок.
13.6.6. Графики в разных системах координат
В пакете plots имеется множество функций для построения графиков в различных системах координат. Объем книги не позволяет воспроизвести примеры на все виды таких графиков, ибо их многие сотни. Да это и не надо — во встроенных в справочную систему примерах можно найти все нужные сведения. Так что ограничимся лишь парой примеров применения функции tubeplot(C, options), позволяющей строить весьма наглядные фигуры в пространстве, напоминающие трубы или иные объекты, образованные фигурами вращения.
На рис. 13.32 показана одна из таких фигур. Она поразительно напоминает раковину улитки. Функциональная окраска достигнута доработкой графика с помощью панели форматирования. Смысл параметра С (в документе Conchoid) легко понять из этого примера.
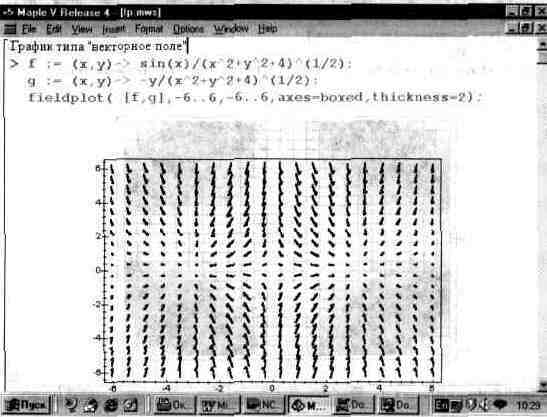
Рис. 13.31. Двумерный график типа векторного поля.
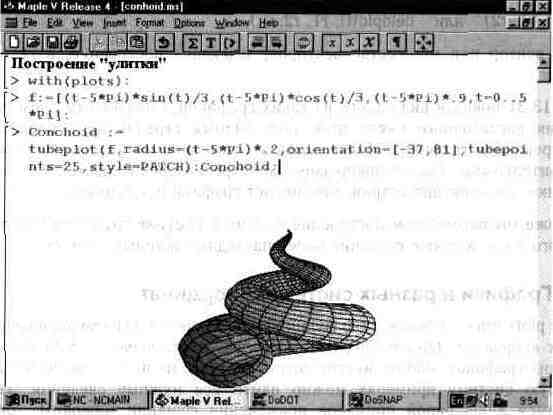
Рис. 13.32. Построение графика «улитки».
Эта функция может использоваться и для построения ряда трубчатых объектов в пространстве. При этом автоматически задается алгоритм удаления невидимых линий даже для достаточно сложных фигур. Это наглядно иллюстрирует пример
на рис. 13.33, показывающий фигуру «цепи». Не правда ли реалистичность этой фигуры поражает воображение?
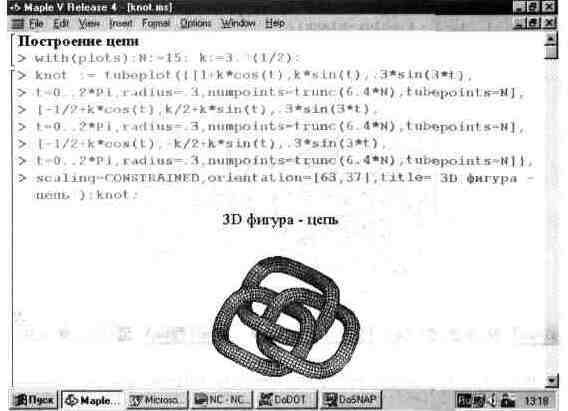
Рис. 13.33. Фигура «цепи», построенная с применением функции tubeplot.
Можно немало размышлять о том, как природа «узнала» о математических закономерностях, положенных в основу тех или иных геометрических объектов, или, возможно, о гениальности людей, сумевших найти такие закономерности для природных объектов. В наше время Maple V открывает огромные возможности для таких людей.
13.6.7. Графики типа трехмерного векторного поля
Наглядность ряда графиков можно существенно увеличить, строя их в трехмерном представлении. Например, для такого построения векторных полей можно использовать графическую функцию fieldplot3d. В отличие от функции fieldplot, она строит стрелки как бы в трехмерном пространстве (рис. 13.34).
Все сказанное об особенностях таких двумерных графиков остается справедливым и для графиков трехмерных. В частности, для получения достаточной их представительности нужно тщательно отлаживать форматы представления таких графиков.
13.6.8. Контурные трехмерные графики
В отличие от векторных графиков, контурные графики трехмерных поверхностей, наложенные на сами эти поверхности, нередко повышают восприимчивость таких поверхностей — подобно изображению линий каркаса. Для одновременного построения трехмерной поверхности и контурных линий на них служит функция contourplot3d. Пример ее применения показан на рис. 13.35.
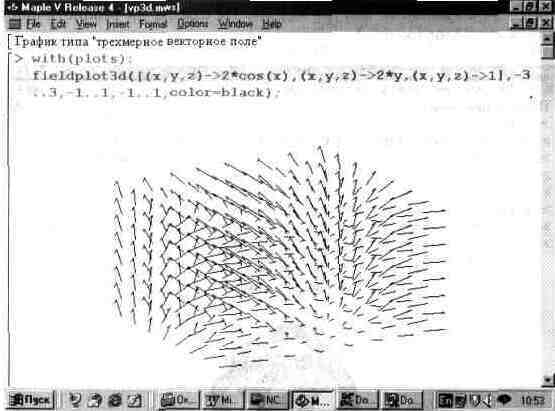
Рис. 13,34. Построение векторного поля в трехмерном пространстве.
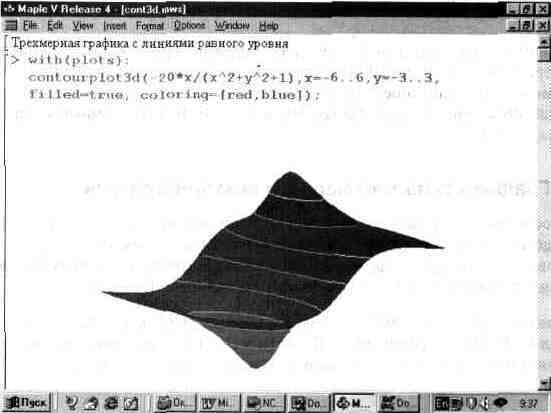
Рис. 13.35. График трехмерной поверхности с контурными линиями.
Для повышения наглядности этот график доработан с помощью панели форматирования графиков. В частности, включена функциональная окраска и подобраны углы обзора фигуры, при которых отчетливо видны впадина и пик фигуры.
13.6.9. Техника визуализации сложных пространственных фигур
Приведенные выше достаточно простые примеры дают представление о высокой степени визуализации геометрических фигур с помощью пакета plots. Здесь мы рассмотрим еще несколько примеров визуализации трехмерных фигур. Многие видели катушки индуктивности, у которых провод того или иного диаметра намотан на тороидальный магнитный сердечник. Математическая абстракция такой катушки показана на рис. 13.36.
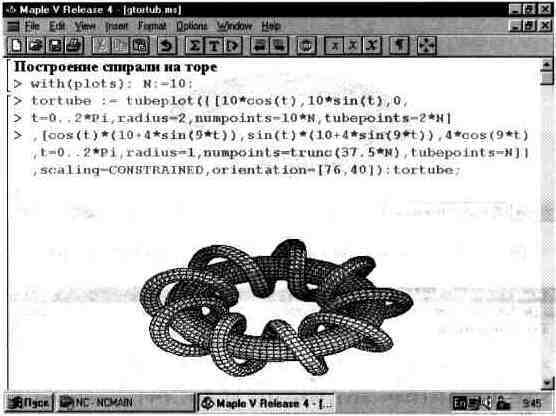
Рис. 13.36. Top с обмоткой — толстой спиралью.
В документе (рис. 13.36) для функции tubeplot использовано довольно большое число параметров-опций. Не всегда их действие очевидно. Поэтому на рис. 13.37 показано построение трех взаимно пересекающихся торов с разными типами их построения. Этот рисунок дает также наглядное представление о возможности построения нескольких графических объектов (представленных функциями р1, р2 и рЗ) с помощью функции tubeplot.
Наконец, на рис. 13.38 показано построение тора с тонкой обмоткой. Рекомендуется внимательно просмотреть запись функции tubeplot в этом примере и в примере, показанном на рис. 13.36. Можно также поэкспериментировать с опциями графика, от которых сильно зависит его представительность и наглядность.
В ряде случаев наглядно представленные фигуры можно строить с применением объединения однотипных фигур. Пример графика подобного рода представлен на рис. 13.39. Здесь готовится список графических объектов s, смещенных по вертикали. С помощью функции display они воспроизводятся на одном графике, что повышает реалистичность изображения.
Последний пример имеет еще одну важную особенность — он иллюстрирует задание графической процедуры, в теле которой используются функции пакета
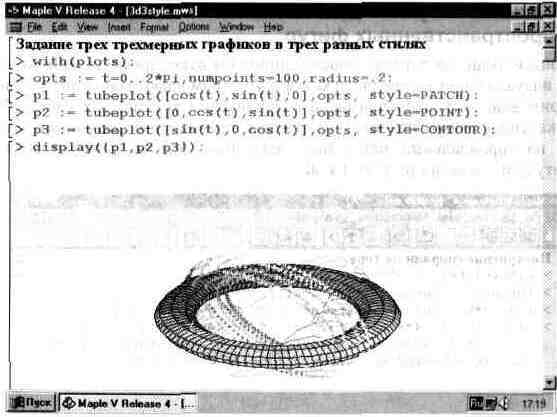
Рис. 13.37. Три пересекающихся тора с разным стилем построения.
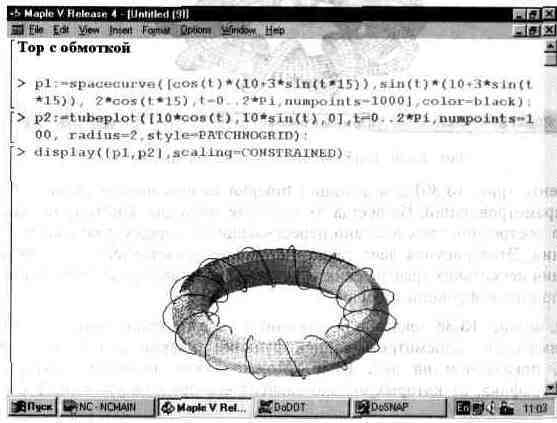
Рис. 13.38. Top с тонкой обмоткой.
plots. Параметр п этой процедуры задает число элементарных фигур, из которых строится полная фигура. Таким образом, высотой фигуры (или шириной «шины») можно управлять. Возможность задания практически любых графических процедур средствами Maple-языка существенно расширяет возможности системы Maple.
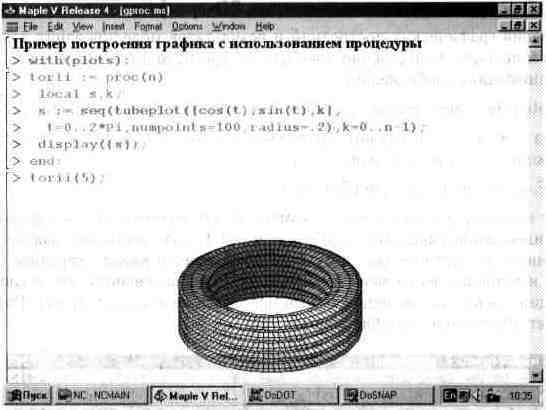
Рис. 13.39. Построение фигуры, напоминающей шину автомобиля.
Наглядность графиков типа графика плотности и векторного поля может быть улучшена их совместным применением. Пример его показан на рис. 13.40.
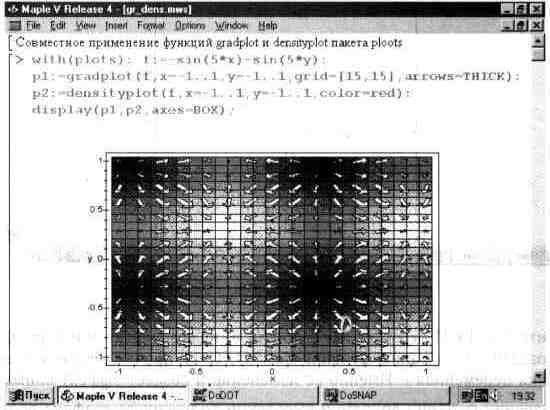
Рис. 13.40. Пример совместного применения графиков плотности и векторного поля.
Этот пример иллюстрирует использование «жирных» стрелок для обозначения векторного поля. Наглядность графика повышается благодаря наложению стрелок на график плотности, который лучше, чем применение стрелок, дает представление о плавности изменения высоты поверхности, заданной функцией f.
13.6.10. Построение анимационных 20-графиков
Визуализация графических построении и результатов моделирования различных объектов и явлении существенно повышается при использовании средств «оживления» (анимации) изображений.
Пакет plots имеет две простые функции для создания анимационных графиков.
Первая из этих функций служит для создания анимации графиков, представляющих функцию одной переменной х — F:
anirnate(F, х, t) или animate(F, х, t,o)
При этом параметр х задает пределы изменения по переменной х, а параметр t — пределы изменения дополнительной переменной t. Суть анимации заключается в построении серии картинок (как в мультфильме), причем каждая картинка (фрейм) связана с изменяемой во времени переменной t. Если надо явно задать число кадров N анимации, то в качестве опции о надо использовать опцию frame=N. Рис. 13.41 показывает применение функции animate.
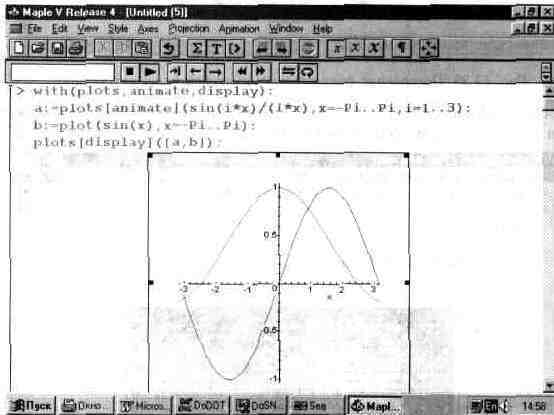
Рис. 13.41. Первый стоп-кадр анимации.
В документе рис. 13.41 строятся две функции — не создающая анимации функция sin(x) и создающая анимацию функция sin(i*x)/(i*x), причем в качестве переменной t задана переменная i. Именно ее изменение и создает эффект анимации.
При исполнении функции animate и выделении полученного графика появляется панель проигрывания анимационных клипов. Она имеет кнопки управления с обозначениями, принятыми у современных магнитофонов. Пустив кнопку пуска (с треугольником, острием обращенным вправо), можно наблюдать изменение вида кривой для функции sin(i*x)/(i*x).
К сожалению, картинки в книгах всегда неподвижны и воспроизвести эффект анимации трудно. Ограничимся приведением еще одного стоп-кадра (рис. 13.42).
Нетрудно заметить, что на нем показана функция sin(i*x)/(i*x) в иной фазе, чем на рис. 13.41.
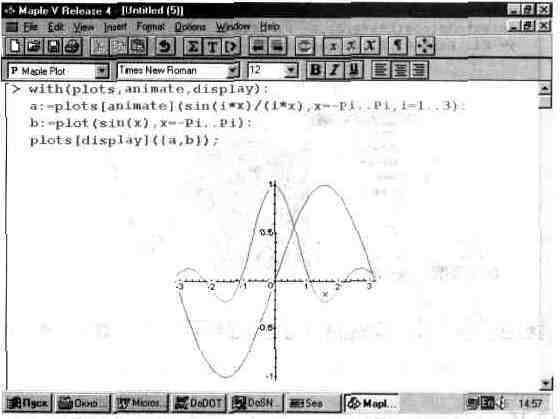
Рис. 13.42. Второй стоп-кадр анимации.
Анимация графиков может найти широкое применение при создании учебных материалов. С ее помощью можно акцентировать внимание на отдельных параметрах графиков и образующих их функций.
13.6.11. Построение анимационных ЗО-графиков
Аналогичным образом может осуществляться и анимация трехмерных фигур. Для этого используется функция animate3d:
animate3d(F,x, y,t,o)
Здесь F — описание функции (или функций), х, у и t — диапазоны изменений переменных х, у и t. Для задания числа кадров N надо использовать необязательную опцию о в виде frame=N.
На рис. 13.43 показано построение анимационного графика. После задания функции, график которой строится, необходимо выделить график и запустить анимационный проигрыватель — как это описывалось для анимации двумерной графики.
На рис. 13.43 показано также контекстно-зависимое меню, которое появляется при нажатии правой клавиши мыши в момент, когда курсор ее находится в поле выделенного графика. Нетрудно заметить, что с помощью этого меню (и открываемых им подменю) можно получить доступ к опциям трехмерной графики и выполнить необходимые операции форматирования, такие, как включение цветовой окраски, выбор ориентации фигуры и т.д.
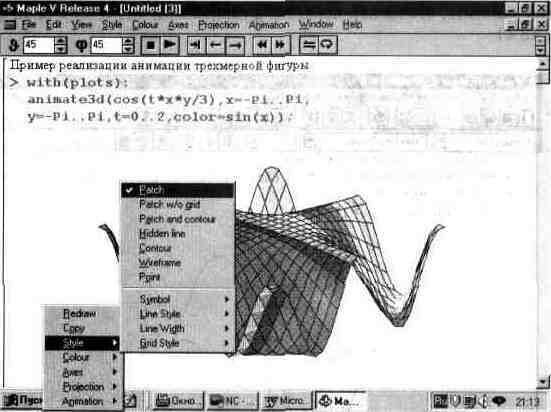
Рис. 13.43. Подготовка анимационного ЗО-графика.
13.6.12. Использование для анимации опции insequence
Еще один путь создания анимационных рисунков — создание ряда графических объектов р1, р2, рЗ и т.д. и их последовательный вывод с помощью функции:
display(pl,p2,p3,...,insequence=true) display3d(pl,p2,p3...,insequence=true)
Здесь основным моментом является применение опции insequence=true. Именно она обеспечивает вывод одного за другим серии графических объектов р1, р2, рЗ и т.д.
13.7. Графика пакета plottools 13.7.1. Состав пакета plottools
Инструментальный пакет графики plottools служит для создания графических примитивов, строящих элементарные геометрические объекты на плоскости и в пространстве: отрезки прямых и дуг, окружности, конусы, кубики и т.д. Его применение позволяет разнообразить графические построения и строить множество графиков специального назначения. В пакет входят следующие графические примитивы:
arc arrow circle cone cuboid curve cutin cutout cylinder disk dodecahedron ellipse ellipticArc hemisphere hexahedron hyperbola icosahedron line octahedron pieslice point polygon rectangle semitorus sphere tetrahedron torus
Вызов примитивов пакета осуществляется после загрузки пакета в память ПК командой with(plottools). Обычно примитивы используются для задания графических объектов, которые затем выводятся функцией display. Возможно, применение этих примитивов совместно с различными графиками.
13.7.2. Примеры применения примитивов пакета plottools
Большинство примитивов пакета plottools имеет довольно очевидный синтаксис. Например, для задания дуги используется примитив
агс(с, г, а..Ь, ...),
где с — список с координатами центра окружности, к которой принадлежит дуга, г — радиус этой окружности, а..Ь — диапазон углов. На месте многоточия могут стоять обычные опции, задающие цвет дуги, толщину ее линии и т.д. Все формы записи графических примитивов и их синтаксис можно найти в справочной системе.
На рис. 13.44 показано применение нескольких примитивов двумерной графики для построения дуги, окружности, закрашенного красным цветом эллипса и отрезка прямой. Кроме того, на графике показано построение синусоиды. Во избежание искажений пропорций фигур надо согласовывать диапазон изменения переменной х.
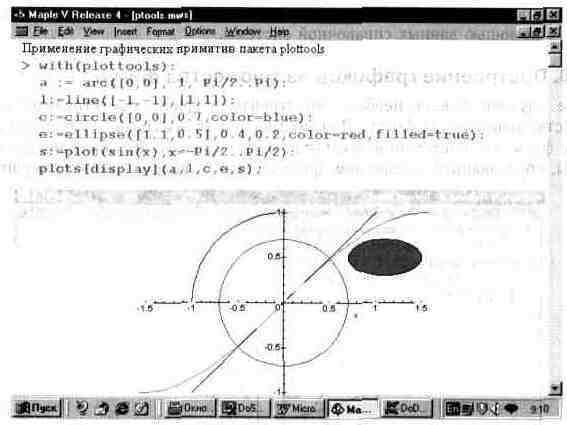
Рис. 13.44. Примеры применения примитивов 20-графики пакета plottools.
Аналогичным образом используются примитивы построения трехмерных фигур. На рис. 13.45 показано совместное построение двух пересекающихся кубов и сферы в пространстве. Нетрудно заметить, что графика пакета приблизительно (с точностью до сегмента фигур) вычисляет области пересечения фигур. С помощью контекстно-зависимого меню правой клавиши мыши (рис. 13.45) можно устанавливать условия обзора фигур, учитывать перспективу при построении и т.д. В частности, фигуры на рис. 13.45 показаны в перспективе.
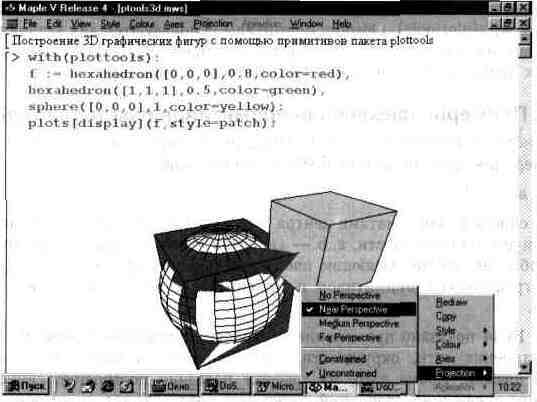
Рис. 13.45. Примеры применения примитивов 30-графики пакета plottools.
С другими возможностями этого пакета читатель теперь справится самостоятельно или с помощью данных справочной системы.
13.7.3. Построение графиков из множества фигур
В ряде случаев бывает необходимо строить графики, представляющие собой множество однотипных фигур. Для построения таких графиков полезно использовать функцию повторения seq(f,i=a..b). На рис. 13.46 показано построение фигуры, образованной вращением прямоугольника вокруг одной из вершин.
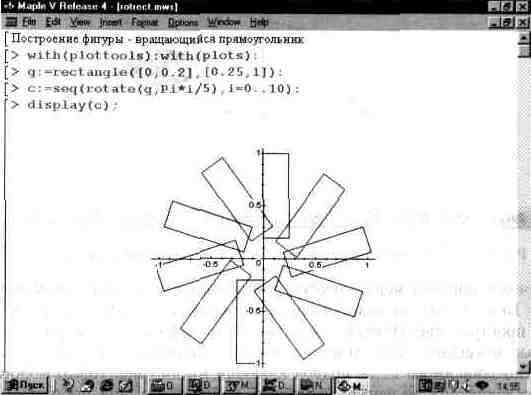
Рис. 13.46. Построение фигуры, образованной вращением прямоугольника.
В этом примере полезно обратить внимание еще и на функцию поворота фигуры — rotate. Именно сочетание этих двух функций (мультиплицирования и поворота базовой фигуры — прямоугольника) позволяет получить сложную фигуру, показанную на рис. 13.46.
13.8. Графическое представление решений дифференциальных уравнений
13.8.1. Применение функции odeplot пакета plots
Для обычного графического представления результатов решения дифференциальных уравнений может использоваться функция odeplot из описанного выше пакета plots. Эта функция используется в следующем виде:
odeplot(s,vars,r,o),
где s — запись (в выходной форме) дифференциального уравнения или системы дифференциальных уравнений, полученных при их численном решении функцией dsolve, vars — переменные, r — параметр, задающий пределы решения (например, а..Ь) и о — не обязательные дополнительные опции.
На рис. 13.47 представлен пример решения одного дифференциального уравнения с выводом решения у(х) с помощью функции odeplot.
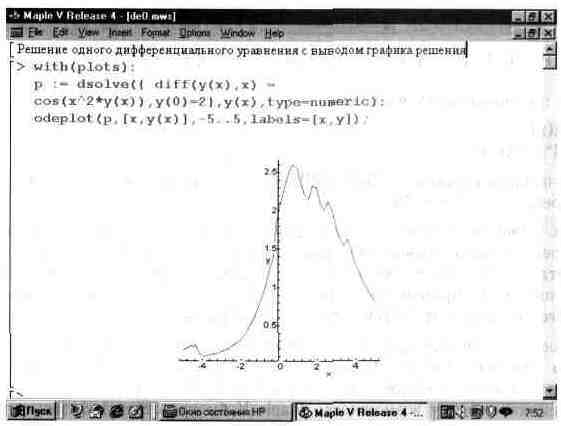
Рис. 13.47. Пример решения одного дифференциального уравнения.
В этом примере решается дифференциальное уравнение y'(x)=cos(x"2*y(x))
при у(0)=2 и х, меняющемся от -5 до 5. Левая часть уравнения записана с помощью функции вычисления производной diff. Результатом построения является график решения у(х).
На другом примере (рис. 13.48) представлено решение системы из двух нелинейных дифференциальных уравнении. Здесь с помощью функции odeplot строятся графики двух функций — у(х) и z(x).
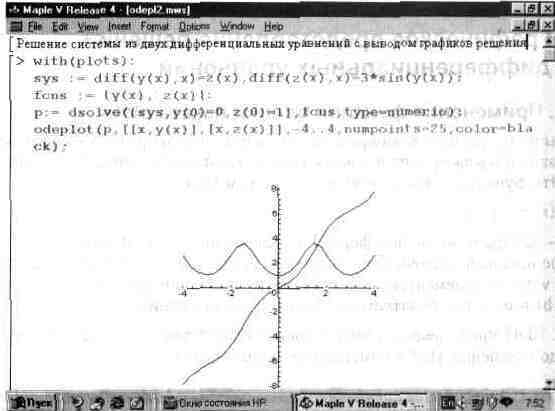
Рис. 13.48. Пример решения системы из двух дифференциальных уравнении
В этом примере решается система:
y'(x)=z(x) z'(x)=3*sin(y(x))
при начальных условиях у(0)=0, z(0)=l и х, меняющемся от -4 до 4 при числе точек решения, равном 25.
Иногда решение системы из двух дифференциальных уравнений (или одного дифференциального уравнения второго порядка) представляется в виде фазового портрета — при этом по осям графика откладываются значения у(х) и z(x) при изменении х в определенных пределах. Рис. 13.49 представляет построение фазового портрета для системы, представленной выше.
Обычное решение, как правило, более наглядно, чем фазовый портрет решения. Однако для специалистов (например, в теории колебаний) фазовый портрет порою дает больше информации, чем обычное решение. Он более трудоемок при построениях, поэтому возможность Maple V быстро строить фазовые портреты трудно переоценить.
13.8.2. Функция DEplot из пакета DEtools
Специально для решения и визуализации решений дифференциальных уравнений и систем с дифференциальными уравнениями служит инструментальный пакет DEtools. В него входит ряд функций для построения наиболее сложных и изысканных графиков решения дифференциальных уравнений. Основной из этих функций является функция DEplot. '
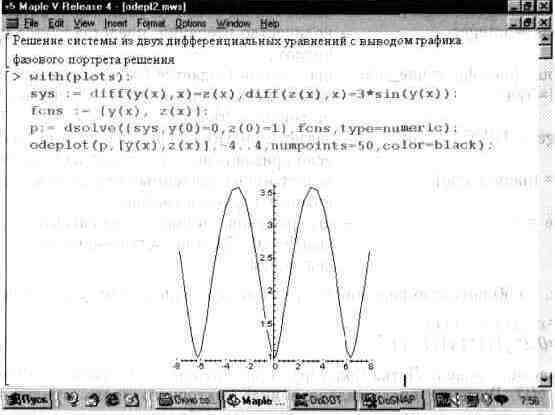
Рис. 13.49. Представление решения системы дифференциальных уравнений в виде фазового портрета.
Функция DEplot может записываться в нескольких формах:
DEplot(deqns, vars, trange, eqns) DEplot(deqns, vars, trange, inits, eqns) DEplot(deqns, vars, trange, yrange, xrange, eqns) DEplot(deqns, vars, trange, inits, xrange, yrange, eqns)
Здесь: deqns — лист (множество) с системой дифференциальных уравнении первого порядка или одиночное уравнение любого порядка, vars — зависимая переменная (лист) либо множество зависимых переменных, trange — область изменения независимой переменной t, inits — начальные условия для решения, yrange — область изменения для первой зависимой переменной, xrange — область изменения для второй зависимой переменной, eqns — опция, записываемая в виде keyword=value. Замена имен переменных другими в данном случае не допустима.
Эта функция обеспечивает численное решение дифференциальных уравнений или их систем при одной независимой переменной t и строит графики решения. Для автономных систем эти графики строятся в виде векторного поля направлений, а для неавтономных систем только в виде кривых решения. По умолчанию реализуется метод Рунге-Кутта 4-го порядка, что соответствует опции method=classi-cal[rk4]. Возможна спецификация и других методов (см. главу 10). В каталоге EXAMPLE системы Maple V R4 можно найти файл deplot.mws с многочисленными примерами применения функции DEplot.
С функцией DEplot могут использоваться следующие опции о:
arrows = type — тип стрелки векторного поля ('SMALL',
'MEDIUM', 'LARGE', 'LINE' или 'NONE');
colour, color = arrowcolour — цвет стрелок (задается 7 способами);
dirgrid = [integer,integer] — число линий сетки (о умолчанию 20(20);
iterations = integer — количество итераций, представленное целым
числом;
linecolour, linecolor = line_info— цвет линии (задается 5 способами);
method='rk4' — задает метод решени 'euler', 'backeuler',
'impeuler' и 'rk4';
obsrange = TRUE,FALSE — задает (при TRUE) прерывание вычислений,
если кривая решения выходит из области обзора;
scene = [name,name] — задает имена зависимых переменных, для
которых строится график;
stepsize = h — шаг решения, по умолчанию равный
abs((b-a))/20, и представленный вещественным
значением.
На рис. 13.50 показано решение системы дифференциальных уравнений
х- (t)=x(t)*(l-y(t)) у' (t)=0,3*y(t)*(x(t)-l),
описывающих модель Лотка-Вольтерра при заданных в документе изменениях t, x(t) и y(t). Решение представлено в виде векторного поля, стрелки которого становятся касательными к кривым решения. Обратите внимание на функциональную закраску стрелок векторного поля.
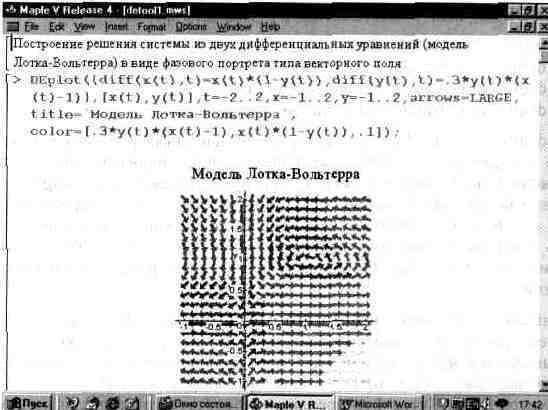
Рис. 13.50. Решение системы дифференциальных уравнении Лотка-Вольтерра с выводом в виде графика векторного поля.
Еще интересней вариант графиков, представленный на рис. 13.51. Здесь помимо векторного поля построены фазовые портреты решения с использованием функциональной закраски их линий. Фазовые портреты построены для двух наборов начальных условий: х(0)= у(0)=1.2 и х(0)=1 и у(0)=0.7.
Следует отметить, что функция DEplot может обращаться к другим функциям пакета DEtools для обеспечения специальных графических возможностей, таких как построение векторного поля или фазового портрета решения.
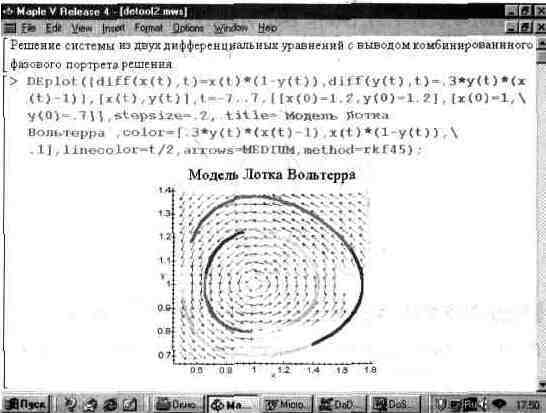
Рис. 13.51. Пример построения двух фазовых портретов на фоне векторного поля.
13.8.3. Функция DEplot3d из пакета DEtools
В ряде случаев решение систем дифференциальных уравнений удобно представлять в виде пространственных кривых — например, линий равного уровня или просто в виде кривых в пространстве. Для этого служит функция DEplot3d.
DEplot3d(deqns, vars, trange, initset, о) DEplot3d(deqns, vars, trange, yrange, xrange, initset, o)
Назначение параметров и опций этой функции аналогично указанному для функции DEplot.
Рис. 13.52 поясняет применение функции DEplot3d для решения системы из двух дифференциальных уравнений с выводом фазового портрета колебаний в виде параметрически заданной зависимости x(t), y(t). В данном случае фазовый портрет строится на плоскости по типу построения графиков линий равной высоты.
Другой пример (рис. 13.53) показывает решение системы из двух дифференциальных уравнений с построением объемного фазового портрета. В этом случае используется координатная система ЗD-гpaфики и графические построения соответствуют параметрическим зависимостям x(t), y(t) и z(t). Вид фазового портрета напоминает разворачивающуюся в пространстве объемную спираль. Функциональная окраска ее делает график эффектным, что, увы, теряется при черно-белом воспроизведении графика.
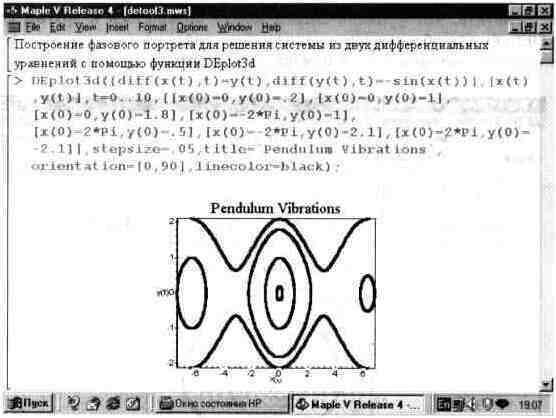
Рис. 13.52. Пример решения системы из двух дифференциальных уравнении с помощью функции DEplot3d.
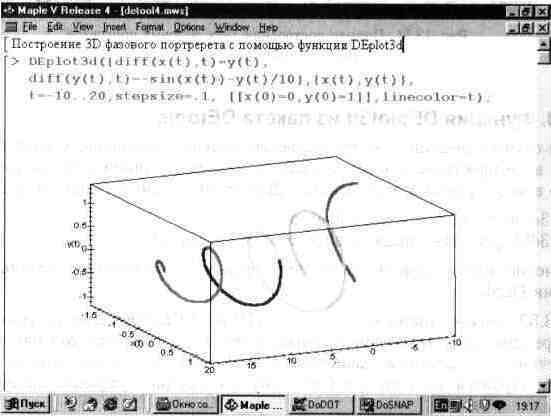
Рис. 13.53. Пример решения системы из двух дифференциальных уравнении с построением трехмерного фазового портрета.
Возможности функции DEplot позволяют решать системы дифференциальных уравнении с числом последних и больше двух — рис. 13.54, например. Однако в этом случае число решений, представляемых графически, выходит за пределы, допустимые ЗИ-графикои. При этом от пользователя зависит, какие из зависимо-
стен опускаются при построении, а какие строятся. Так, на рис. 13.54 в пространстве построены две кривые решения.
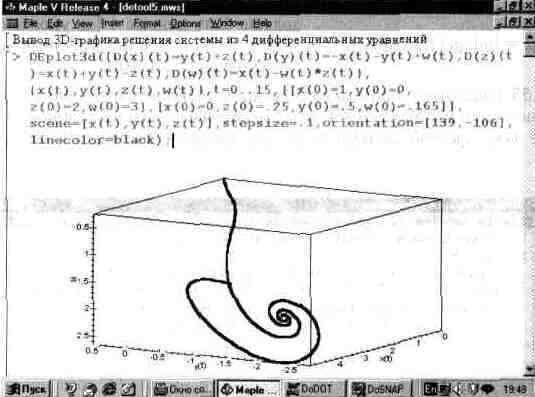
Рис. 13.54. Решение системы из четырех дифференциальных уравнении.
Нередко таким образом можно вывести на построение и иные зависимости. Однако их число обычно приходится ограничивать из-за потери наглядности графика при большом числе линий.
13.8.4. Функция PDEplot пакета DEtools
Еще одна функция пакета DEtools — DEtools[PDEplot] служит для построения графиков решения систем с квазилинейными дифференциальными уравнениями первого порядка в частных производных:
Р(х,у,и) * D[l](u)(x,y) + Q(x,y,u) * D[2](u)(x,y) = R(x,y u),
так что
P их + Q uy = R,
где P, Q и R зависят только от х, у и и(х,у), при этом dx/dt = P, dy/dt = Q, du/dt = R.
Эта функция используется в следующем виде:
PDEplot(pdiffeq, var, Lcurve, srange, о) PDEplot(pdiffeq, var, i_cLirve, srange, xrange, yrange, urange, o)
Здесь, помимо отмеченных ранее параметров, pdiffeq — квазилинейные дифференциальные уравнения первого порядка (PDE), vars — независимая переменная и Lcurve — начальные условия для параметрических кривых ЗО-поверхности. Помимо опций, указанных для функции DEplot, здесь могут использоваться следующие опции:
basechar = TRUE,FALSE,ONLY — устанавливает показ базовых характеристик кривых;
basecolour, basecolor = b_colour — устанавливает цвет базовых характеристик;
initcolour, initcolor = Lcolour — инициализация цветов;
numchar = integer — задает число отрезков кривых, которое не
должно быть меньше 4 (по умолчанию 20);
numsteps = [integerl,integer2] — задает число шагов интегрирования
(по умолчанию [10,10]).
Рис. 13.55 показывает применение функции PDEplot. Этот пример, взятый из справочной системы Maple V R4, показывает, насколько необычным может быть решение даже простой системы дифференциальных уравнений в частных производных.
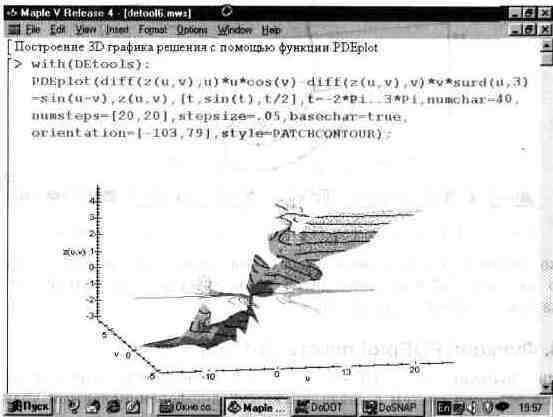
Рис. 13.55. Пример применения функции PDEplot.
В данном случае решение представлено трехмерной фигурой весьма нерегулярного вида.
Другой пример использования функции PDEplot показан на рис. 13.56. Он иллюстрирует комбинированное построение графиков решения разного типа с применением функциональной закраски, реализуемой по заданной формуле с помощью опции initcolor.
Еще раз отметим, что, к сожалению, рисунки в данной книге не дают представления о цвете. Поэтому наглядность решений, видимых на экране дисплея, существенно выше.
13.8.5. Графическая функция dfieldplot
Графическая функция dfieldplot служит для построения векторного поля (поля направления) по результатам решения дифференциальных уравнений. Фактически эта функция как бы входит в функцию DEplot и при необходимости вызывается последней. Но она может использоваться и самостоятельно, что показывает
рис. 13.57, на котором показан пример решения следующей системы дифференциальных уравнений: x'(t)=x(t)*(l-y(t)), y'(t)=0.3*y(t)*(x(t)-l).
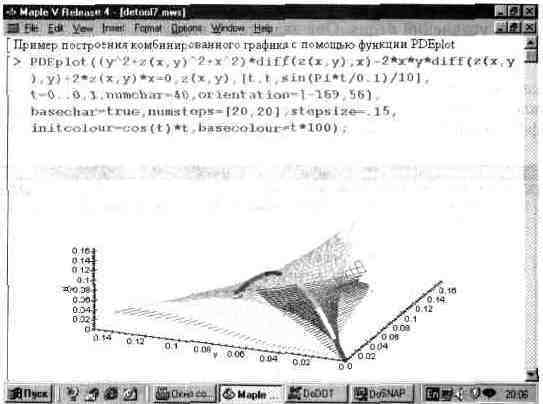
Рис. 13.56. Построение комбинированного графика с помощью функции PDEplot.
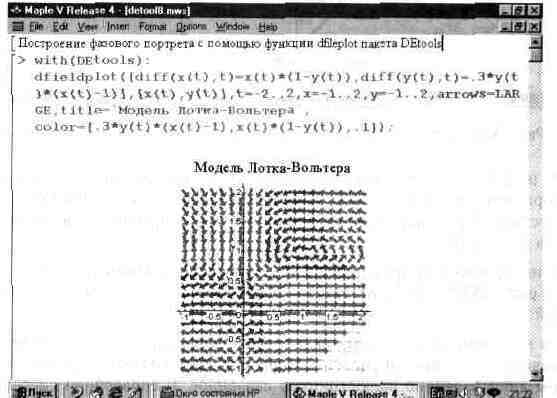
Рис. 13.57. Построение фазового портрета в виде графика векторного поля.
Обратите внимание на использование опций в этом примере, в частности на вывод надписи на рисунок на русском языке. В целом список параметров функции phaseportrait аналогичен таковому для функции DEplot (отсутствует лишь задание начальных условий).
13.8.6. Графическая функция phaseportrait
Графическая функция phaseportrait служит для построения фазовых портретов по результатам решения одного дифференциального уравнения или системы дифференциальных уравнений deqns. Она задается в виде:
phaseportrait(deqns, vars,trange,inits,o)
При задании уравнений достаточно указать их правые части. На рис. 13.58 представлен пример применения функции phaseportrait для решения системы из трех дифференциальных уравнений первого порядка.
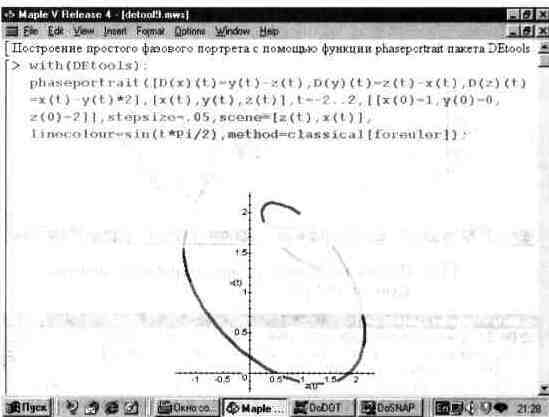
Рис. 13.58. Построение фазового портрета с помощью функции phaseportrait.
В этом примере система дифференциальных уравнений задана с применением оператора дифференцирования D. Функциональная окраска линии фазового портрета достигается использованием опции linecolor, в правой части которой задана формула для цвета.
Еще более интересный пример решения дифференциального уравнения представлен на рис. 13.59. Здесь построены фазовые портреты для асимптотических решений.
В целом надо отметить, что возможности визуализации решений дифференциальных уравнений с помощью системы Maple V весьма велики и приведенные выше примеры лишь частично иллюстрируют сказанное. В справочной системе можно найти ряд других весьма эффектных решений систем дифференциальных уравнений с визуализацией последних.
13.9. Иллюстративная графика пакета student
Пакет student имеет три графические функции для иллюстрации интегрирования методом прямоугольников:
leftbox(f(x), x=a..b, о) или leftbox(f(x), x=a..b, n, 'shading'=<color>, o) rightbox(f(x), x=a..b, о) или rightbox(f(x), x=a..b, n, o) middlebox(f(x), x=a..b, о) или middlebox(f(x), x=a..b, n, o),
Здесь: f(x) — функция переменной х, х — переменная интегрирования, а — левая граница области интегрирования, b — правая граница области интегрирования, n — число показанных прямоугольников, color — цвет прямоугольников, о — опции (см. plot,options).
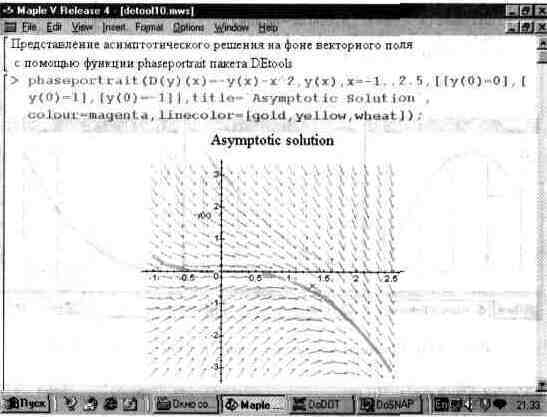
Рис. 13.59. Построение асимптотического решения на фоне графика векторного поля.
В этих функциях прямоугольники строятся соответственно слева, справа и посередине относительно узловых точек функции f(x), график которой также строится. Кроме того, имеется функция для построения касательной к заданной точке х=а для линии, представляющей f(x):
showtangent (f(x), х = а).
Рис. 13.60 показывает все эти возможности пакета student. Четыре вида графиков здесь построены в отдельных окнах.
Возможности графики пакета student ограничены. Но они дают как раз те возможности, которые отсутствуют в основных средствах графики.
13.10. Графика статистического пакета stat
Статистический пакет stat имеет свою 'небольшую библиотечку для построения графиков. Она вызывается в следующем виде:
stats[statplots, function](args) или statplots[function](args)
Вид графика задается описанием function: boxplot, histogram, notchedbox, quantile, quantile2, scatterld, scatter2d и symmetry. Эти функции обеспечивают построение
типовых графиков, иллюстрирующих статистические расчеты. В качестве примера на рис. 13.61 показано задание множества случайных точек и их построение на плоскости в ограниченном прямоугольником пространстве.
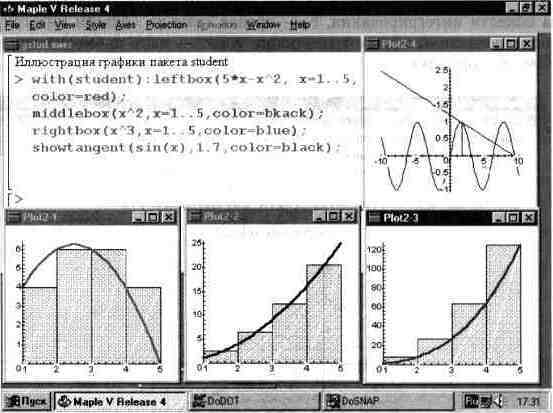
Рис. 13.60. Примеры иллюстративной графики пакета student,
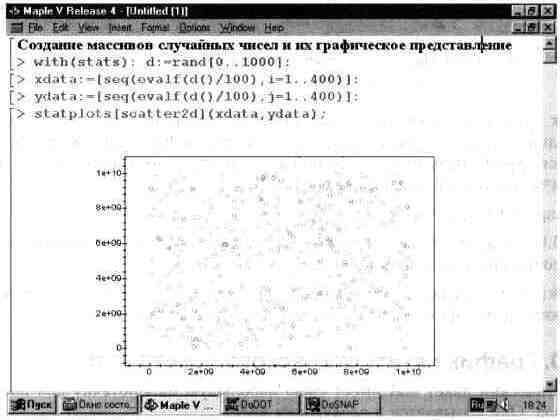
Рис. 13.61. Создание случайных точек и построение их на плоскости.
По равномерности распределения точек можно судить о качестве программного генератора случайных чисел, встроенного в Maple V.
Другой пример применения графических средств пакета stat показан на рис. 13.62. Здесь, помимо изображений, заданных точками в виде маленьких ромбов (тип diamond), представлено изображение специальных объектов, по виду напоминающих радиодетали.
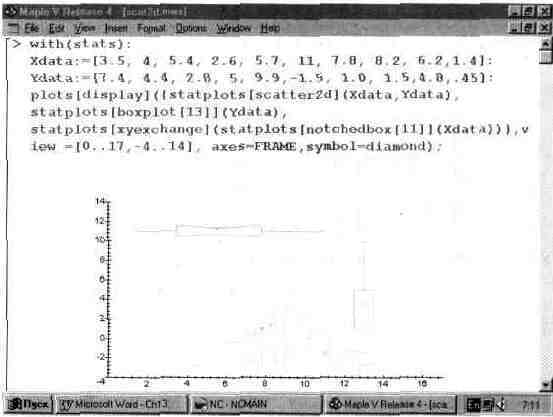
Рис. 13.62. Построения с помощью пакета stats.
Довольно часто используются графики гистограмм. Для их построения пакет stat имеет функцию histogram:
statsfstatplots, histogramj(data) statplots[histogram](data) statsfstatplots, histogram[scale](data) statplots[histogram[scale](data)
Здесь: data — список данных, scale — число или описатель. Детали применения этой простой функции поясняет рис. 13.63. На нем дано два примера — для построения столбцов заданной ширины и высоты и построения распределения 100 случайных чисел с нормальным распределением.
Обратите внимание на то, что в деталях гистограммы для второго примера построенные гистограммы будут несколько меняться от пуска к пуску. Это связано со случайностью генерируемых чисел и небольшими расхождениями в нормальном распределении чисел.
13.11. Графическая визуализация решений и анимация
Выше уже не раз графика использовалась для визуализации решений математических задач. Так, многие особенности даже функций одной переменной вида f(x) могут быть выявлены с помощью графика функций. Затем можно точно вычислить корни функции (точки перехода через 0), экстремумы, крутизну наклона (произ-
водную) в заданных точках и т.д. Еще более информативна в этом отношении трехмерная графика — для большинства функций двух переменных вида z(x,y) нужно очень богатое математическое воображение, чтобы представить их вид — особенно в одной из многих десятков координатных систем.
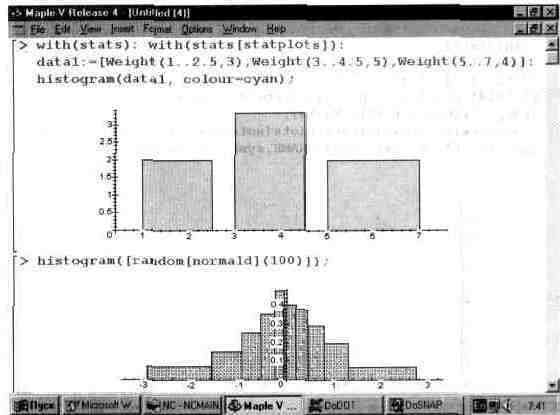
Рис. 13.63. Построение гистограмм.
Однако некоторые виды графиков трудно представить себе даже при наличии такого воображения. В этом отношении Maple V предоставляет поистине уникальные возможности в обеспечении простой и быстрой визуализации решений. Ниже мы рассмотрим несколько наиболее характерных примеров такой визуализации. В них нет наиболее показательных примеров визуализации решений дифференциальных уравнений, поскольку они уже были рассмотрены.
13.11.1. Иллюстрация решения систем линейных уравнений
Системы линейных уравнений могут решаться как с помощью функции solve, так и с помощью матричных методов. Замечательной возможностью функции solve является возможность решения относительно ограниченного числа переменных. Например, систему линейных уравнений с переменными х, у, z, t и v можно решить относительно только первых трех переменных х, у и z. При этом решения будут функциями относительно переменных t и v и можно построить наглядный график решения (рис. 13.64).
На рис. 13.64 система задана пятью равенствами: е1, е2, еЗ, е4 и е5. Затем функцией solve получено вначале решение для всех переменных (для иллюстрации), а затем для трех переменных х, у и z. Для получения решения в виде списка, а не множества, как в первом случае для всех переменных, использована функция подстановки subs. После этого функция plot3d строит плоскость решения в пространстве.
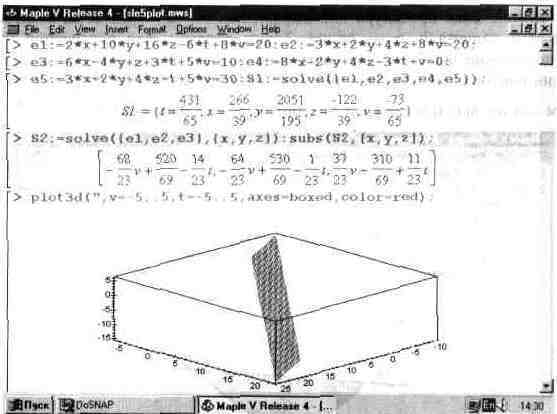
Рис. 13.64. График, представляющий решения системы линейных уравнений.
13.11.2. Графическая визуализация решения системы неравенств
Пожалуй, еще более полезным и наглядным является визуализация решения системы уравнений в виде неравенств. В пакете расширения plots имеется специальная графическая функция inequal, которая строит все граничные линии неравенств и позволяет раскрасить разделенные ими области различными цветами:
inequal(ineqs, xspec, yspec, options).
Параметры этой функции: ineqs — одно или более неравенство или равенство или список неравенств или равенств, xspec — xvar == min_x..max_x, yspec — yvar = min_y..max_y и о — необязательные опции, например указывающие на цвета линий, представляющих неравенства или равенства, и областей, образованных этими линиями и границами графика. Пример применения этой функции представлен на рис. 13.65.
Обратите внимание на задание опций цветов: optionsfasfeasibly задает цвет внутренней области, для которой удовлетворяются все неравенства (равенства), optionsopen и optionsclose задают цвета открытых и закрытых областей графика, optionsexcluded для цвета внешних областей. График дает весьма наглядную интерпретацию действия ряда неравенств (или равенств).
13.11.3. Конформные отображения на комплексной плоскости
Объем данной книги не позволяет объяснить столь тонкое понятие, как конформные отображения на комплексной плоскости. Ограничимся лишь указанием на то, что в пакете plots имеется функция для таких отображений:
conformal(F,rl ,г2,о);
где F — комплексная процедура или выражение, rl, r2 — области, задаваемые в виде а..Ь или name=a..b, о — опции. Таким образом, для построения нужного графика достаточно задать нужное выражение и области изменения rl и г2. Пример построения конформных изображений для трех выражении дан на рис. 13.66.
В данном случае все три графика построены в отдельных окнах.
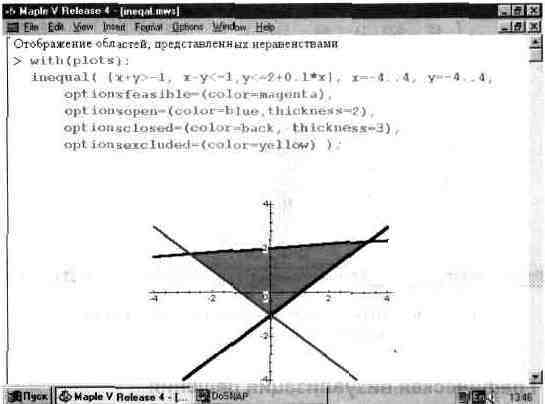
Рис. 13.65. Пример графической интерпретации решения системы неравенств.
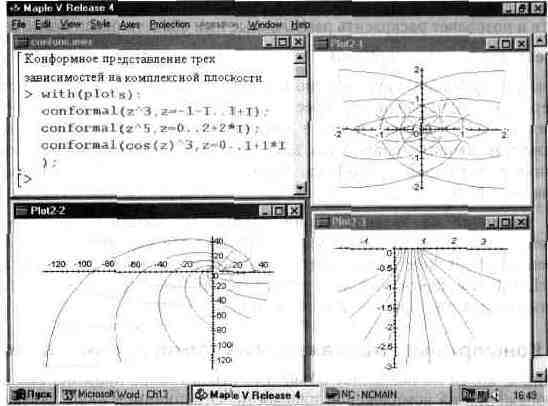
Рис. 13.66. Конформное отображение на комплексной плоскости графиков трех зависимостей.
13.11.4. Графическое представление содержимого матрицы
Многие вычисления имеют результаты, представляемые в форме матриц. Иногда такие результаты можно наглядно представить графически, например, в виде столбиковой диаграммы. Она представляет собой множество столбиков квадратного сечения, расположенных на плоскости, образованной осями строк (row) и столбцов (column) матрицы. При этом высота столбцов определяется содержимым ячеек матрицы.
Такое построение обеспечивает графическая функция matrixplot из пакета расширения plots. На рис. 13.67 показано совместное применение этой функции с двумя функциями пакета linalg, формирующими две довольно экзотические матрицы А и В.

Рис. 13. 67. Графическое представление матрицы
На рис. 13.67 показана графическая визуализация матрицы, полученной как разность матриц А и В. Для усиления эффекта восприятия применяется цветовая функциональная закраска. Для задания цвета введена процедура F.
13.11.5. Визуализация Ньютоновых итераций
Теперь займемся довольно рискованным экспериментом — наблюдением Ньютоновых итераций с их представлением на комплексной плоскости. На рис. 13.68 задана функция f(z) комплексного аргумента. Для этого используется итерационное выражение. Проследить за поведением функции на комплексной плоскости позволяет графическая функция complexplot3d из пакета plots.
Наблюдаемая картина весьма необычна и свидетельствует о далеко не простом ходе итерационного процесса. Риск работы с этим примером заключается в том, что иногда он ведет к фатальным ошибкам, ведущим к прекращению работы с системой. Обычно при пуске этого примера сразу после загрузки системы Maple V такого не происходит, но когда память загружена другими примерами, сбой
вполне возможен. Рекомендуется записывать подобные примеры на диск перед ик запуском. •

Рис. 13.68. Наблюдение за процессом Ньютоновых итерации в ЗО-пространстве.
13.11.6. Визуализация корней случайных полиномов
Наряду с традиционной для математических и статистических компьютерных систем возможностью генерации случайных чисел, Maple V предоставляет довольно «экзотическую» возможность генерации случайных полиномов с высокой максимальной степенью. Для этого используется функция:
ranpoly(var,o)
Она возвращает случайный полином переменной var, причем максимальная степень полинома птах может указываться опцией о вида degree=nmax.
Приведем пример генерации случайного полинома с максимальной степенью 50:
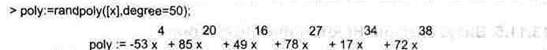
Поскольку полученный полином случайный, то вам не удастся повторить его генерацию — каждый запуск randpoly дает новый полином. Так что важно понять в принципе осуществляемые далее действия. Прежде всего найдем список корней полинома S:
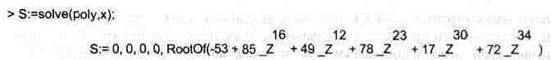
В этом примере обратите внимание на число нулей в начале списка — их надо исключать из дальнейших вычислений. Это, и получение корней в виде обычных
комплексных чисел, делается с помощью функции allvalues, в которой в качестве
параметра надо использовать S[5]. Ниже показано создание списка SA корней полученного выше полинома:
>SA:=[S[1],S[2],S[3],S[4],allvalues(S[5])];
ЗА := [0, 0, 0, 0, -1.010550161 - .1475724933 I,
-1.010550161 + .1475724933 I, -.9465649833,
-.9003773676 - .5534775311 , -.9003773676 + .5534775311 ,
-.8562982808 - .3789548397 , -.8562982808 + .3789548397 ,
-.7320300364 - .6478720727 , -.7320300364 + .6478720727 ,
-.5900687567 - .7989860949 , -.5900687567 + .7989860949 .
-.3987161272-.8962702262 ,-.3987161272 + .8962702262 ,
-.3642724499-.9481481280 ,-.3642724499 + .9481481280 ,
-.02839255705 - .9363196855 I, -.02839255705 + .9363196855 I, .05710128939 -1.018443049 I, .05710128939 + 1.018443049 I, .2868399179-.9808645873 , .2868399179 + .9808645873 , .4149289767-.8396518590 , .4149289767 + .8396518590 , .6775641178-.8099749786 , .6775641178 + .8099749786 , .6864940076 - .6957907203 , .6864940076 + .6957907203 , .8450577013-.4872509104 , .8450577013 + .4872509104 , .9089753119-.3749374155 , .9089753119 + .3749374155 , .9157897832, 1.019132014 - .2114677899I, 1.019132014+.21146778991]
Напоминаем, что эти корни также являются случайными. Теперь можно построить комплексные корни полученного случайного полинома в виде точек на комплексной плоскости:
>with(plots):complexplot(SA,x~1.2..1.2,style=point);
Этот график показан на рис. 13.69.
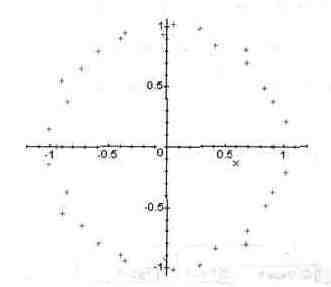
Рис. 13.69. Расположение корней случайного полинома на комплексной плоскости.
Можно заметить любопытную закономерность — точки, представляющие корни случайного полинома укладываются вблизи окружности единичного радиуса с центром в начале координат. Является ли это действительно свойством случайных полиномов или дело в специфике их генерации средствами Maple V — для большинства из нас неясно. Однако этот пример, приводимый в большинстве книг по Maple V, показывает, что порою вычисления могут давать довольно неожидан-
ные результаты. Кстати говоря, аналитически можно вычислять корни полинома с максимальной степенью не более четырех.
Приведенные примеры дают весьма наглядное представление о больших возможностях визуализации решений самых различных задач в системе Maple V. Можно значительно повысить ее, эффектно используя описанные ранее приемы анимации (оживления) изображений. В целом надо отметить, что графические возможности Maple V дают новый уровень качества графики современных математических систем, о котором с десяток лет тому назад можно было только мечтать.
13.11.7. Анимация разложения импульса в ряд Фурье
Анимация (оживление) изображений является одним из самых мощных средств визуализации результатов моделирования тех или иных зависимостей или явлений. Порою изменение во времени одного из параметров зависимости дает наглядное представление о его сути.
Здесь мы расширим представление об анимации и рассмотрим не вполне обычный пример, описанный в [38], — наблюдение за синтезом импульсного сигнала, разложенного в ряд Фурье с числом гармоник N. На рис. 13.70 представлен документ, реализующий такое разложение и синтез для числа гармоник О, 1, 2,..., N.
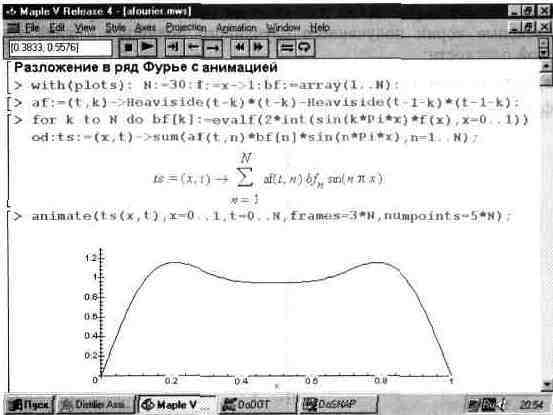
Рис. 13.70. Первый стоп-кадр анимации разложения импульса в ряд Фурье.
Надо полагать, что читатель уже может разобраться в деталях задания прямоугольного импульса — меандра с помощью функции Хевисайда (Heaveside) и его синтеза с помощью ряда Фурье. Соответствующие и достаточно простые выражения представлены на рис. 13.70.
Нетрудно заметить, что при выделении рисунка рамкой появляется анимацион-ный проигрыватель, который позволяет запустить анимацию. Стоп-кадр на приведенном рисунке соответствует началу анимации.
поверхности cos(t*x*y/3), представленной функцией трех переменных t, x и у. При этом изменение первой переменной создает фазы поверхности.
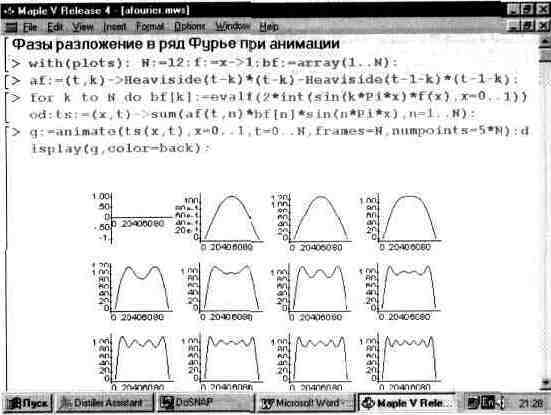
Рис. 13.72. Иллюстрация получения всех фаз анимации 20-графика.
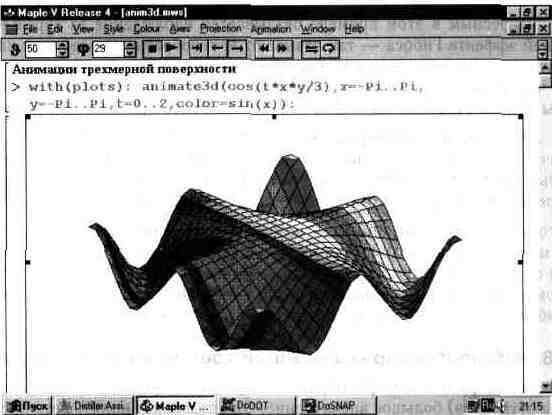
Рис. 13.73. Анимация ЗО-поверхности.
Применение анимации дает повышенную степень визуализации решений ряда задач, связанных с построением двух- и трехмерных графиков. Следует отметить, что анимационные графики для построений требуют дополнительных и достаточ-
но существенных затрат оперативной памяти. Поэтому злоупотреблять числом стоп-кадров таких графиков нельзя.

Рис. 13.74. Фазы анимации ЗО-поверхности.
Глава 14. Математическая система Maple V R5
14.1. Комплект поставки и установка системы
К моменту завершения рукописи данной книги новейшая версия Maple V R5 появилась в коммерческом варианте, но на Internet-странице фирмы Waterloo Maple по ней были приведены строго дозированные данные. Очевидно, фирма пока опасалась бурной рекламы нового продукта — пример вполне достойный подражания, поскольку несвоевременное описание программного продукта, проходящего стадию, апробации чревато серьезными ошибками. Многие из нас сталкивались с этим — «поспешишь, людей насмешишь».
Тем не менее фирма Waterloo Maple no первой же просьбе автора предоставила ему новую реализацию своего программного продукта. Благодаря этому появилась возможность познакомить читателя с основными особенностями новейшей реализации Maple V R5 еще до того, как Maple V R4 сошла устарела. Важно отметить, что эта реализация R5 пока не реализована на всех платформах — например, для ПК класса Macintosh пока последней остается реализация R4.
В этой главе вы познакомитесь с основными достоинствами новой реализации и ее отличиями от предшествующей. Здесь уместно еще раз обратить внимание читателя, что весь материал глав 2 — 13 в равной мере относится как к реализациям R3 и R4, так и R5.
Прежде всего отметим, что новая реализация (Maple V R5) поставляется на двух CD-ROM (но в одной упаковке). В комплект поставки входят две объемные книги — учебник по работе с системой [37] и пособие по программированию [38]. Кроме того, поставляются документы по регистрации системы и брошюра с перечнем книг, изданных по системе Maple V за рубежом.
На первом CD-ROM размещена собственно система, а на другом — библиотека расширения SHARE. Они инсталлируются отдельно — вначале система, а затем библиотека. Никаких проблем с инсталляцией Maple V R5 в среде Windows 95 OSR 2 у автора не возникло. Надо лишь учесть, что для установки новой версии на жестком диске необходимо свободное пространство около 80 Мбайт. По окончании инсталляции в меню программ появляется группа, посвященная установленной системе. Она показана на рис. 14.1.
При запуске системы (позиция меню Maple V Release 5) вначале появляется временное титульное окно с краткими данными о системе и сроках ее разработки. Это окно на фоне рабочего стола Windows 95 представлено на рис. 14.2. Нетрудно заметить, что выпуск данной версии системы датирован ноябрем 1997 года, таким образом, мы описываем программный продукт, только-только появившийся на рынке (эти слова пишутся в начале апреля 1998 года).
Вид экрана при работе с системой Maple V R5 с загруженным демонстрационным документом показан на рис. 14.3. С первого взгляда он почти ничем не отличается от экрана, который виден при работе с реализацией R4. Разве что можно отметить
новую позицию Spreadsheets в главном меню, да и ту пока видную в характерном «тумане» (т.е. в данный момент недоступную).
Рис. 14.1. Папка с компонентами Maple V R5 на рабочем столе Windows 95 OSR 2.

Рис. 14.2. Временное титульное окно системы на рабочем столе Windows 95 OSR 2.
В целом надо сказать, что ничего революционного в новой версии нет и ее основные возможности вполне соответствуют описанным ранее в главах 1 — 13. Тем не менее ряд новых возможностей, естественно, есть, и мы остановимся на их описании ниже. Следует обратить внимание на то, что некоторые из новых возможностей (электронные таблицы, перенос объектов и трансформация графи-
А вот вместо знака " (кавычка) для задания эволюции предшествующего выражения в Maple V R5 используется знак % (процент). Можно применять до трех таких знаков. Эта тонкость в первый момент сбивает с толку пользователей прежних версий Maple V, но к этому быстро привыкаешь.
Существенно повысилась роль управления системой с помощью мыши. Теперь, как во всех приличных Windows-приложениях, ее правая клавиша при нажатии выводит контекстно-зависимое меню, содержащее доступные по контексту операции (они будут рассмотрены более подробно ниже). Это позволяет реализовать метод работы «ввел выражение — нажал кнопку — получил результат». В частности, можно выполнить сразу доступные для заданного выражения символьные преобразования, быстро построить график функции с титульными надписями и т.д.
Реализован в Maple V R5 и принцип «Drag and Drop» (Тащи и Отпускай). Для выделенного объекта, нажав левую клавишу мыши и удерживая ее нажатой, можно перетащить объект на новое место, например на другую строку в данном или в другом документе (при условии, что окна документов развернуты и видны одновременно на экране). Для установки объекта на новое место достаточно отпустить левую клавишу мыши. Таким образом, обеспечивается механизм объектной связи, известный, как OLE 2. В процессе перетаскивания маркер мыши превращается в жирную окружность, перечеркнутую символом \ в исходном блоке, или в обычный курсор мыши с туманным прямоугольником у основания при переходе в иной блок (куда объект переносится).
Если вы хотите, перетаскивая объект, оставить его и на прежнем месте, то делайте это при нажатой клавише Ctrl. В этом случае к упомянутому туманному прямоугольнику добавляется отметка в виде маленького крестика. Заметим, что объектом могут быть не только целые выражения, но и их части или даже группы объектов — словом, все, что может быть выделено.
14.3. Работа с электронными таблицами
Одно из важных отличий Maple V R5 от предшествующих версий — это возможность работы с электронными таблицами. Для задания электронных таблиц в главном меню в позиции Insert появилась операция Spreadsheets (вставка шаблона электронной таблицы). При исполнении этой операции появляется типичный шаблон электронной таблицы (рис. 14.4).
Нетрудно заметить, что вид электронной таблицы вполне соответствует типовому для современных программ класса табличных процессоров, например Exel из пакета Microsoft Office. Таким образом, произошло сближение математической системы Maple V с еще одним важным классом программ.
Как обычно, в ячейки таблиц могут вводиться числовые денные (рис. 14.4). Ячейки характеризуются своим адресом — буквой столбца и номером строки. Внутри таблицы курсор мыши превращается в жирный крест и его можно использовать для указания нужной ячейки и фиксации в ней ввода. При этом ввод данных в выделенную ячейку производится их набором в специальной инструментальной строке для работы с таблицами (поле ввода занимает цбольшую часть этой панели). Нажав правую клавишу мыши, можно вывести контекстно-зависимое меню с рядом операций, доступных для заданной ячейки.
Рис. 14.4. Шаблон электронной таблицы.
Для работы с таблицами в главном меню Maple V R5 появилась отдельная позиция Spreadsheets (рис. 14.5). Она содержит набор операций, обеспечивающих работу с табличными данными.
Рис. 14.5. Вид экрана Maple V R5 с открытой позицией Spreadsheets главного меню.
Как видно из рис. 14.5, в состав этой позиции входят следующие операции:
| Evaluate Selection | Эволюция выражения в выделенной ячейке. |
| Evaluate Spreadsheet | Эволюция выражений по всем ячейкам таблицы. |
| Row | Работа со строками (вставка, удаление и т.д.). |
| Column | Работа со столбцами (вставка, удаление и т.д.). |
| Fill | Заполнение ячеек (в том числе автоматическое в заданном направлении). |
| Properties | Просмотр свойств ячеек. |
| Show Border | Включение или выключение показа обрамления таблицы. |
| Resize to Grid | Выделение таблицы для изменения ее размеров. ¦ |
Возможности Maple V R5 в обработке табличных данных намного превосходят общеизвестные из опыта работы с обычными табличными процессорами. Последние мы не будем рассматривать, так как по ним имеется много литературы и заинтересованный пользователь легко разберется с соответствующими возможностями Maple V R5. Отметим лишь принципиально новые возможности — работы с символьными данными в ячейках таблицы. Это иллюстрируется рис. 14.6.
Рис. 14.6. Работа с символьными данными в электронной таблице.
Таблица на рис. 14.6 содержит три столбца: с исходными выражениями, записью инертной формы интеграла, в подынтегральную функцию которого входит исходное выражение и экспоненциальный множитель и исполняемая запись интеграла. Обратите внимание на запись интеграла в строке ввода и в самой таблице.
Например, для записи инертной формы интеграла в строку ввода надо ввести следующую запись:
Int(exp(x)*'A5,x).
Это означает задание вывода интеграла с подынтегральной функцией в виде е"х, умноженной на содержимое ячейки А5, причем А — положение столбца, а 5 — номер строки. Таким образом, А5 есть адрес ячейки, из которой (указано символом ~) выбирается заданное выражение. Исполнив команду эволюции для этой ячейки (или для всей таблицы), можно получить выражения в следующих двух позициях справа от выбранной ячейки.
14.4. Использование палитр математических символов
Отдельные палитры ввода (или наборные панели), выводимые в любое место экрана по желанию пользователя, были введены в ряд современных математических систем (например, MathCAD 6.0/7.0 и Mathematica 3) и показали себя весьма удобными средствами пользовательского интерфейса, позволяющими вводить специальные знаки и символы (шаблоны операций) простым их указанием курсором мыши и нажатием ее левой кнопки. Теперь такие палитры приобрела и система Maple V R5 (рис. 14.7).
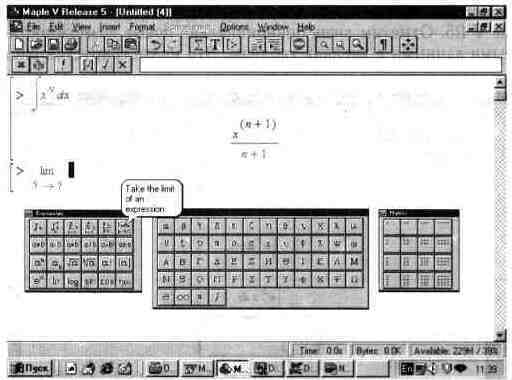
Рис. 14.7. Работа с палитрами математических символов и операции.
К сожалению, заполнение шаблонов в операторах, выбранных с помощью палитр, константами и именами переменных, все же приходится выполнять в поле ввода, подтверждая их ввод нажатием клавиши Enter. Да и набор символов в палитрах ограничен, а сами они выглядят мелковато даже при стандартном разрешении дисплея 640х480 пикселей. На рис. 14.8 показана отдельно палитра ввода математических символов и операторов.
Рис. 14.8. Палитра ввода математических символов и операторов.
На рис. 14.9 показана еще одна палитра — на этот раз для ввода больших и малых греческих букв. Она заметно облегчает ввод таких букв, широко используемых для обозначении математических констант и переменных. Ранее для ввода греческих букв приходилось применять специальные комбинации клавиш, а в реализации R5 теперь достаточно просто указать нужную букву курсором мыши и щелкнуть ее левой клавишей.

Рис. 14.9. Палитра греческих букв.
Имеется также палитра ввода матриц. Она показана на рис. 14.10. С ее помощью можно быстро вводить шаблоны матриц различного размера — от одного до шестнадцати элементов в матрице. Возможно задание также векторов различного типа — в строку и в столбец.

Рис. 14.10. Палитра ввода шаблонов матриц.
Удобство применения палитр связано с тем, что их можно поместить в любом (обычно наиболее удобном) месте документа и вводить соответствующие математические знаки, символы или шаблоны простыми и удобными средствами (с помощью мыши). В верхнем левом углу каждой палитры имеется единственная небольшая кнопка со знаком «-» в прямоугольнике. Она служит для закрытия палитры после того, как отпала необходимость вводить имеющиеся в ее составе знаки. Закрывать неиспользованные палитры целесообразно, поскольку они занимают место в окне документа и могут мешать его обзору.
Итак, можно сделать вывод, что альянс разработчиков MathCAD (фирма MathSoft Inc.) с фирмой Waterloo Maple для последней оказался плодотворным — помимо включения ядра Maple V в новые версии систем класса MathCAD, в новую реализацию Maple V R5 были включены палитры для многих математических символов и операций.
14.5. Трансформация графиков в реальном масштабе времени
В Maple V R5 введена новая и безусловно важная возможность — трансформация ЗО-графиков в реальном масштабе времени. В прежних версиях выделенный
график заменялся параллелограммом, который можно было вращать мышью. Однако сам график на время трансформации просто исчезал и для его перестройки надо было запускать пиктограмму с буквой R (Redraw). Процесс перестройки графика даже на достаточно производительных ПК (класса Pentium 200) шел несколько секунд.
Похоже, разработчикам новой реализации системы удалось существенно ускорить алгоритмы перестройки ЗО-графиков, что позволило реализовать вращение фигур в пространстве в реальном масштабе времени. Рис. 14.11 показывает, как это происходит.
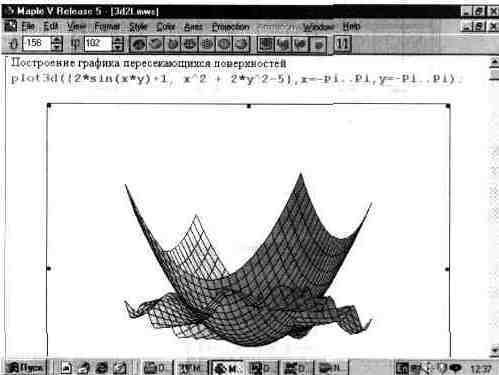
Рис. 14.11. Трансформация SD-графика в реальном масштабе времени.
Хотя некоторая инерционность процесса перестройки заметна даже при работе на ПК с процессором Pentium 200 ММХ и с ОЗУ 32 Мбайта, ощущение от реального поворота фигуры остается вполне отчетливым. Эта возможность позволяет быстро найти оптимальный угол зрения на фигуру, при которой ее особенности, например пики и впадины, выявляются в наиболее полной мере. Заметно существенное улучшение и алгоритма построения линий пересечения сложных фигур в пространстве. Наглядная и эффектная функциональная окраска фигур выполняется теперь по умолчанию.
К сожалению, при использовании созданных ранее в реализации R4 сложных графических объектов (в виде нескольких компонентов) этот алгоритм иногда дает сбои. Пример такого случая показан на рис. 14.12. В данном случае тор вращается сам по себе, в результате обмотки оказываются не на нем, а где-то в стороне.
Возможно, что это вызвано именно тем, что исходный документ готовился в предшествующей реализации системы. Кстати, при попытке загрузки файла от предшествующей реализации системы выводится окно с предупреждающей надписью и предлагает преобразовать файл в формат, присущий новой реализации. Это окно показано на рис. 14.13.
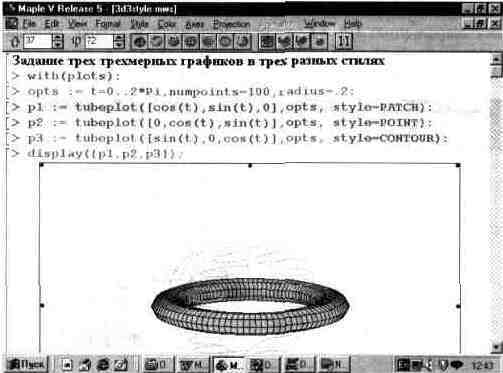
Рис. 14.12. Сбои трансформации сложного ЗО-объекта.
Ответьте «Да», если вы намерены преобразовать файл, и «Нет» при отказе от этой операции. В целом можно считать, что Maple V R5 вполне обеспечивает совместимость файлов документов с предшествующей версией системы.
Рис. 14.13. Окно, сообщающее о загрузке файла предшествующей реализации и необходимости его преобразования.
14.6. Контекстно-зависимое меню операций
Сторонников легкой работы с системой (надеемся, что и вы, читатель, относитесь к таковым) порадует еще одна, хотя и не принципиальная, но очень полезная возможность — контекстно-зависимое меню операций (в том числе математических). Она реализуется нажатием правой клавиши мыши при указании маркером мыши заданного объекта.
На рис. 14.14 показан экран системы и контекстно-зависимое меню, относящееся к введенному выражению sin(x)/x, находящемуся в строке вывода. При этом меню дает перечень операций, которые можно делать с этим выражением — например, дифференцировать, интегрировать, строить график и т.д.
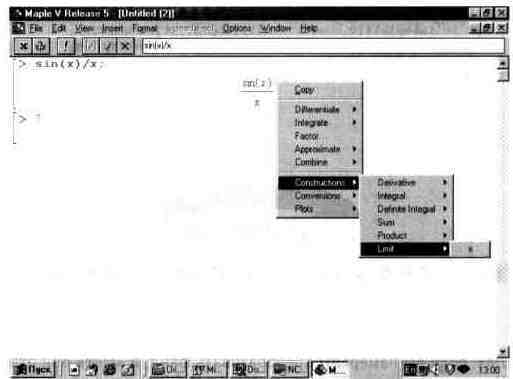
Рис. 14.14. Контекстно-зависимое меню для математических выражении.
Если маркер мыши стоит в строке ввода, то появляется меню, представляющее основные операции по работе с текстами. Окно этого меню показано на рис. 14.15. Вводимые им операции не нуждаются в особых комментариях.

Рис. 14.15. Меню для работы с текстами
Применение контекстно-зависимых меню облегчает работу с системой и делает ее похожей на работу в среде современных программных средств под Windows 95. В целом оно реализует принцип «ввел выражение — нажал кнопку — получил результат».
14.7. Быстрое построение графиков
Быстрое построение 2D- и ЗО-графиков — еще одна приятная «мелочь» новой реализации Maple V R4, облегчающая визуализацию вычислений. Ее тоже можно реализовать с помощью контекстно-зависимого меню. Достаточно вызвать его для выбранного выражения, как с помощью операции Plot можно построить график. При этом система Maple V R5 сама определяет (по виду выражения), какой же график надо строить.
Рис. 14.16 показывает быстрое построение графика функции sin(x) /x указанным способом. При этом вам даже не надо помнить, какой функцией обеспечивается построение графика. В дальнейшем оформление графика можно изменить операциями форматирования.
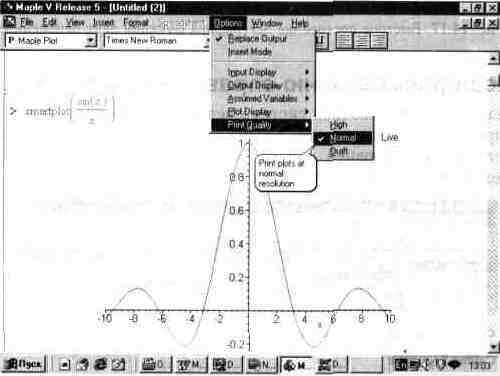
Рис. 14.16. Быстрое построение 20-графика функции одной переменной.
Кстати говоря, в позиции главного меню Options появилась новая операция Print Quality — качество печати (рис. 14.16). Она позволяет выбрать три степени качества печати: High (высшее). Normal (нормальное) и Draft (черновое).
Столь же просто обстоит дело с построением иных графиков. Так, на рис. 14.17 представлено построение ЗО-графика функции двух переменных — sin(x*y/5). При этом можно воспользоваться описанным ранее приемом — трансформацией графика в реальном масштабе времени для получения наивысшей выразительности графика.
Maple V R5 имеет ряд дополнительных функций для такого рода построений. Две из них видны на рис. 14.16 и 14.17. Это функции smartplot и smartplot3d. С другими можно ознакомиться с помощью справочной системы.
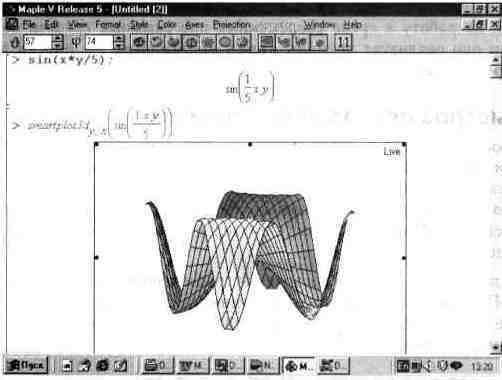
Рис. 14.17. Быстрое построение SD-графика функции двух переменных.
14.8. Расширяемое меню справочной системы
Уже отмечалось, что справочная система реализации R5 вновь приобрела характер расширяемого тематического поиска, реализованного с помощью меню, содержащего до пяти уровней поиска. Это хорошо видно при просмотре рис. 14.18, на котором показан сеанс работы со справочной системой.
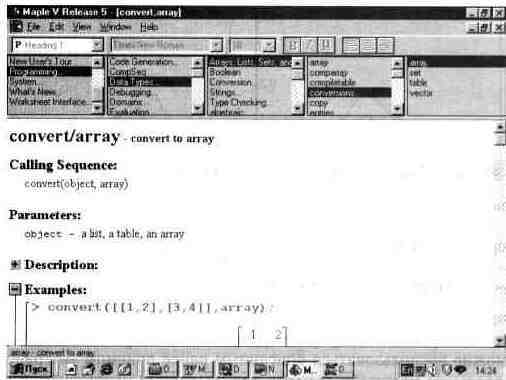
Рис. 14.18. Работа со справочной системой Maple V R5.
Maple V R5 имеет также обучающую систему и справку по новым возможностям. Они реализованы аналогично основной справочной системе. Описание всех справочных компонентов дано на английском языке, но оно настолько лаконично,
что многие детали описания вполне понятны даже для пользователей, имеющих начальные и средние уровни владения английским языком.
14.9. Подготовка HTML-файлов для передачи по сети Internet
Пожалуй, одним из самых важных отличий реализации R5 стала возможность подготовки в ней полноценных HTML-файлов, которые можно передавать по сети Internet. Maple V и ранее позволял использовать в своих документах гиперссылки, которые являются основой формата файлов HTML. Однако средства записи (экспорта) файлов в этом формате появились только в реализации Maple V R5.
Для подготовки HTML-файлов сначала в среде Maple V R5 готовится обычный документ. Затем для записи его используется операция Export As... (рис. 14. 19). В появившемся подменю надо выбрать позицию HTML.
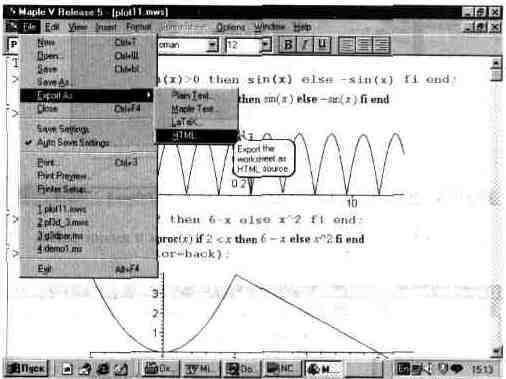
Рис. 14.19. Подготовка к записи документа в формате HTML.
После выбора указанной позиции появляется окно для выбора места записи файла (диска, папки) и задания имени файла. Выполнив эти операции, надо активизировать кнопку ОК в окне (рис. 14.20).
В процессе записи HTML файлов Maple переводит рисунки в формат GIF с 256 цветами. Текст файлов (включая математические выражения) преобразуется в форматы, применяемые в языке HTML описания файлов для сети Internet. Заметим, что этот формат поддерживает некоторые из возможностей Maple-документов, такие, как гипертекстовые ссылки и указания на взаимное расположение различных объектов документов.
На рис. 14.20 показан вид созданного таким образом документа в окне одного из самых распространенных Internet-браузеров — Microsoft Internet Explorer. Нетрудно заметить, что все элементы документа воспроизводятся нормально без искажений и нарушений взаимного расположения.
Если документ содержит гиперссылки или имеет так называемую электронную форму (с заголовками в отдельном окне), то эти элементы сохраняются и формируются электронные заголовки документа. При отсутствии заголовков в этом окне отображается имя файла. Подготовка документов в формате HTML значительно расширяет возможности обмена документами по сети Internet и организации совместной работы над сложными математическими проектами.
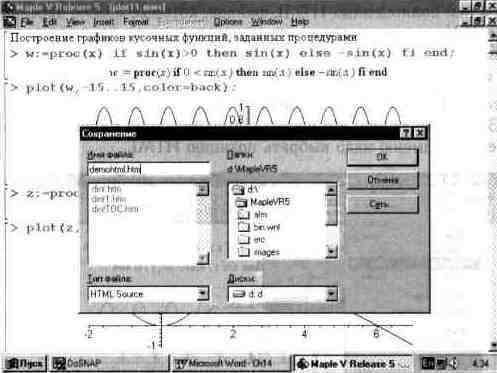
Рис. 14.20. Окно для указания места записи и имени файла.
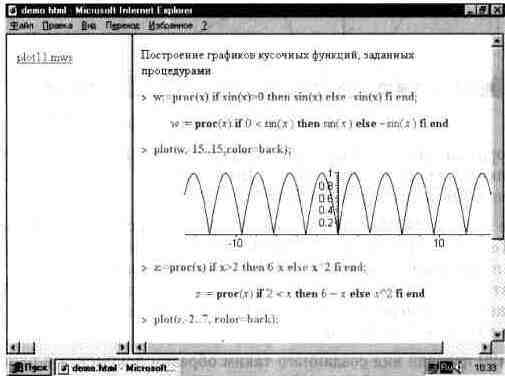
Рис. 14.21. Вид Maple-документа в окне браузера Microsoft Internet Explorer.
14.10. Интеграция с системой MatLAB 5.0
Многим пользователям математических систем хорошо знакома интерактивная система MatLAB фирмы MathWorks, Inc. (США, г. Нейтик, штат Массачусетс) [13,14,36]. Ее название происходит от слов Matrix Laboratory — матричная лаборатория. За многие годы своего развития эта система стала мировым лидером среди систем, ориентированных на численные расчеты, которые она выполняет заметно быстрее многих других систем. Новая версия MatLAB 5.0 это шедевр вычислительной математики. Она имеет огромное число поклонников во всем мире, несмотря на то, что ее стоимость (в варианте под Windows) приближается к трем тысячам долларов!
Было бы неразумно пытаться обойти эту мощную систему в части эффективности выполнения численных расчетов — особенно матричных. Поэтому разработчики ряда других математических систем избрали более тонкий и умный путь — интеграции с MatLAB.Так и система Maple V R5 автоматически интегрируется с MatLAB 5.0 при установке обеих систем на ваш ПК.
Maple V R5 имеет довольно большое число функций системы MatLAB 5.0, которые вызываются как библиотечные функции пакета matlab. После этого они становятся доступными для применения в документах Maple V R5 — совместно с имеющимися в последней системе функциями.
14.11. Internet-страница фирмы Waterloo Maple
Internet — глобальная сеть мирового значения, своей электронной паутиной WWW (World Wide Web) охватившая весь земной шар. По существу это совокупность огромного числа компьютерных сетей, работа в которых происходит по специальным согласованным протоколам, обеспечивающим высокую вероятность передачи информации конечному абоненту при выходе из строя многих ветвей связи. Для подключения к сети Internet владелец современного ПК должен установить на нем модем и через него подключиться к обычной телефонной сети. Это делается с помощью организации — провайдера, предоставляющей за определенную плату услуги Internet. Для обзора сети Internet и организации связи (например, электронной почты E-mail) служат специальные программы — брау-зеры, примеры работы с которыми уже приводились.
Получив доступ к Internet пользователь приобщается к огромному океану разнообразной информации. Она обычно имеет вид гипертекстовых страниц (сайтов). Каждая страница имеет свой уникальный адрес. Здесь мы кратко рассмотрим лишь страницу фирмы Waterloo Maple — разработчика систем класса Maple V. На рис. 14.22 показана так называемая домашняя страница этой маститой фирмы. Обратите внимание, что в строке адреса браузера Microsoft Internet Explorer 4.0 (кстати именуемого уже обозревателем) указан адрес данной страницы.
Эта страница дает доступ к другим подчиненным ей страницам, например бесплатного программного обеспечения (Download), серийных продуктов (Products), сообщений прессы (Press), сведения о корпорации Maple Software (Corporate), данных о книгах по системе (Library) и др. Эти страницы несут огромный объем информации — например, в странице Library можно найти данные и аннотации по сотням книг по системе Maple V, изданных за рубежом и разбитым на ряд разделов (математика, физика, электротехника, механика, астрономия и
т.д.). На рис. 14.23 показан результат поиска информации о системе Maple V R5 на странице Products (продукты).
Рис. 14.22. Домашняя страница фирмы Maple Software.
Рис. 14.23. Начало раздела с данными о новейшей реализации системы Maple V R5.
Многих пользователей (особенно наших) особенно заинтересует раздел с названием Download. Он открывает доступ к так называемому файловому серверу FTP, с которого можно вполне легально (а главное бесплатно!) переписать самое разнообразное программное обеспечение: демонстрационные и рабочие версии различных программных продуктов, библиотеки их расширения, инструменталь-
ные средства для отладки и многое другое. На рис. 14.24 представлена одна из страниц FTP сервера фирмы Maple.
Рис. 14.24. Одна из страниц FTP-сервера фирмы Maple Software.
Внизу этой страницы, кстати, хорошо видно предложение о копировании Maple V R4, занимающей в упакованном виде 2348 Кбайт. Мы обращаем внимание на это в связи с тем, что (к сожалению) далеко не всякая электронная почта в Internet способна «перекачать» на жесткий диск ПК файл такого размера. Да и время «перекачки» достигает около часа даже при вполне приличном модеме. Сам процесс перекачки очень нагляден и показан на рис. 14.25. Файл, который перекачивается на диск, ассоциируется с листком бумаги, перелетающим из папки в FTP-сервсрс в папку на жестком диске ПК.
Рис. 14.25. Иллюстрация перекачки файла с FTP-сервера на жесткий диск ПК.
Страницы фирмы Maple содержат адреса электронной почты как самой фирмы, так и сотрудничающих с ней фирм и даже отдельных лиц. Так что вы, имея доступ в Internet, можете наладить полезные связи с зарубежными приверженцами системы Maple V и приступить к совместному выполнению интересных и полезных проектов.
На страницах фирмы можно найти последние новости о модернизации выпущенных программных продуктов и о разработке новых, данные о проводимых семинарах и иных мероприятиях. Можно даже найти предложения о работе на фирме в качестве разработчика программных продуктов или менеджера по их реализации.