Контрольная работа: Интегрирование и производная функций

Задание 1

Осуществить интерполяцию с помощью полинома Ньютона исходных данных из табл. 1 вычислить значение интерполяционного полинома в точке .

Таблица 1

	Порядковый номер исходных данных
№	1	2	3	4	5	6	7	8	9	10
Х	1,415	1,420	1,425	1,430	1,435	1,440	1,445	1,450	1,455	1,460
У	0,888	0,889	0,89	0,891	0,892	0,893	0,894	0,895	0,896	0,897

интерполяция погрешность производная

Решение

Интерполяционный многочлен Ньютона для равноотстоящих узлов записывается в виде

- конечная разность первого порядка

- конечная разность К-го порядка.

Таблица конечных разностей для экспериментальных данных:


1	1,415	0,888	0,001	0	0	0	0	0	0	0	0
2	1,420	0,889	0,001	0	0	0	0	0	0	0
3	1,425	0,89	0,001	0	0	0	0	0	0
4	1,430	0,891	0,001	0	0	0	0	0
5	1,435	0,892	0,001	0	0	0	0
6	1,440	0,893	0,001	0	0	0
7	1,445	0,894	0,001	0	0
8	1,450	0,895	0,001	0
9	1,455	0,896	0,001
10	1,460	0,897

Задание 2

Уточнить значение корня на заданном интервале тремя итерациями и найти погрешность вычисления.

, [0,4].

Решение

Вычислим первую и вторую производную функции

. Получим и .

Итерационное уравнение запишется так:

В качестве начального приближения возьмем правый конец отрезка .

Проверяем условие сходимости:

Условие сходимости метода Ньютона выполнено.

Таблица значений корня уравнения:

i
1	3,083
2	2,606
3	2,453

Уточненное значение корня .

В качестве оценки абсолютной погрешности полученного результата можно использовать величину

Задание 3

Методами треугольников, трапеций и Симпсона вычислить определенный интеграл.

Решение

Метод прямоугольников

Значение интеграла на интервале определяется следующей формулой:

	слева	справа
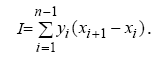
1	0,25	0,2
2	0,2	0,1667
3	0,1667	0,1429
4	0,1429	0,125
	0,7595	0,6345

Значение интеграла: .

Метод трапеций

Площадь трапеции равняется полусумме оснований, умноженной на высоту, которая равна расстоянию между точками по оси х. интеграл равен сумме площадей всех трапеций.


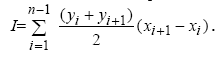
1	0,25
2	0,2
3	0,1667
4	0,1429
5	0,125

Значение интеграла: .

Метод Симпсона


1	0,25
2	0,2
3	0,1667
4	0,1429

Значение интеграла: .

Задание 4

Проинтегрировать уравнение методом Эйлера на интервале [0.2, 1.2] . Начальное условие у(0,2)=0,25.

Решение

Все вычисления удобно представить в виде таблицы:


0	0,2	0,2500	0,2751	0,0688	0,3188
1	0,45	0,3188	0,4091	0,1023	0,4211
2	0,7	0,4211	0,5634	0,1408	0,5619
3	0,95	0,5619	0,7359	0,1840	0,7459
4	1,2	0,7459	0,9318	0,2329

Таким образом, задача решена.

Задание 5

Задача 1. Вычислить сумму и разность комплексных чисел, заданных в показательной форме. Переведя их в алгебраическую форму. Построить операнды и результаты на комплексной плоскости.

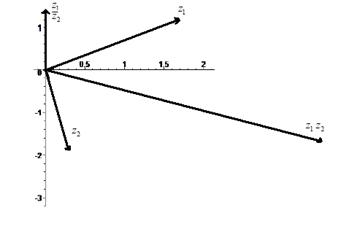
Задача 2. Вычислить произведение и частное комплексных чисел. Операнды и результаты изобразить на комплексной плоскости.

Решение

Задача 1.

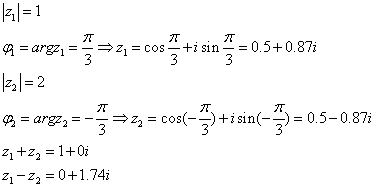
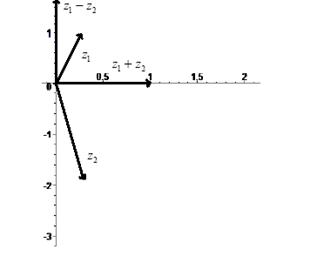
Задача 2.

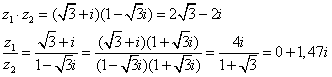
Задание 6

Вычислить производную функции f(z) в точке .

Решение

Так как для аналитических функций справедливы все формулы и правила дифференцирования действительного аргумента, то

Задание 7

Вычислить интеграл по замкнутым контурам а) и б), считая обход контура в положительном направлении. Нарисовать область интегрирования, указать на рисунке особые точки.

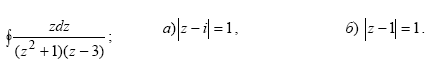
Решение

а)

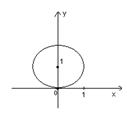
Подынтегральная функция имеет особые точки: . Тогда интеграл вычистится по следующей формуле:

б)

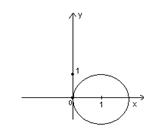
Подынтегральная функция имеет особые точки: . Тогда интеграл вычистится по следующей формуле: