Контрольная работа: Системи лінійних рівнянь

Контрольная работа: Системи лінійних рівнянь

СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ

1. Основні поняття і теореми

Постановка задачі. Потрібно знайти значення х1, х2, … , хn , що задовольняють таким співвідношенням: .

Тут aij (i = 1, 2, … , m; j = 1, 2, … , n) і bk (k = 1, 2, … , m) – задані числа.

При цьому: ; ; .

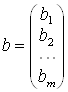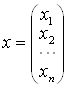Матриця А називається головною матрицею системи, вектор b – вектором-стовпцем правих частин, вектор x – вектором-стовпцем невідомих.

Використовуючи ці позначки, можна систему записати в матричній формі: Ах = b.

Якщо b1 = b2 = ¼ = bm = 0, то система рівнянь називається однорідною. Якщо хоча б одне з bk (k = 1, 2, ¼ , m) відмінне від нуля, то система називається неоднорідною.

.

Матриця  називається розширеною матрицею системи.

Якщо система має хоча б один розв’язок, то вона називається сумісною.

При цьому система, що має єдиний розв’язок, називається визначеною, а більше одного розв’язку – невизначеною.

Якщо система не має розв’язків, то вона називається несумісною.

При розв’язуванні систем лінійних рівнянь має бути знайдена відповідь на три запитання:

А. Чи сумісна система?

В. Чи визначена система?

С. Як знайти розв’язок (чи розв’язки) системи, якщо вони існують?

Правило Крамера. Якщо неоднорідна система рівнянь невироджена (detА ¹ 0), то система визначена, тобто має єдиний розв’язок, і його можна знайти за формулами Крамера:  (k = 1, 2, … , n) де Dk – визначник матриці, яку можна одержати, якщо в матриці А системи k-й стовпець замінити на стовпець вільних членів.

Ранг матриці. З розв’язуванням систем рівнянь безпосередньо пов'язане поняття рангу матриці. Ранг матриці – це найвищий порядок її мінора, відмінного від нуля.

Для того щоб знайти ранг матриці, важливо орієнтуватися в тому, які перетворення з матрицею можна робити, не змінюючи при цьому її ранг:

1) транспонування;

2) перестановка двох рядків (стовпців);

3) множення всіх елементів рядка (або стовпця) на число a ¹ 0;

4) додавання до всіх елементів рядка (стовпця) відповідних елементів іншого рядка (стовпця);

5) вилучення нульового рядка (стовпця);

6) викреслення рядка (стовпця), що є лінійною комбінацією інших рядків (стовпців).

Однорідні системи. Розглядається однорідна система лінійних рівнянь з n невідомими: Ах = 0.

Якщо rangА = n (detА ¹ 0), то система визначена і має тільки тривіальний розв’язок: x1 = x2 = … = xn = 0.

Якщо rangА < n (detА = 0), то система має не тільки тривіальні розв’язки. При цьому всі розв’язки однорідної системи рівнянь утворюють лінійний простір L і dim L = n – rangА.

Щоб знайти базис простору розв’язків однорідної системи рівнянь, треба:

1.Знайти базисний мінор матриці А.

2.Якщо рядок не входить до базисного мінора, то рівняння, яке йому відповідає, є лінійною комбінацією інших рівнянь, і його можна не брати до уваги.

3.Якщо стовпець не входить у базисний мінор, то невідома з відповідним номером призначається вільною. Усього знайдеться (n – rang A) вільних невідомих.

4.Нехай вільні невідомі хr+1, хr+2, … , хn. Якщо дати вільним невідомим довільні значення, то одержимо неоднорідну систему рівнянь відносно хr+1, хr+2, … , хn , у якої визначник не дорівнює нулю, і, отже, система має єдиний розв’язок.

5.Дамо вільним невідомим значення (1, 0, 0, 0, … , 0), потім (0, 1, 0, 0, … , 0) і т. д. Розв’язуючи системи, що утворюють, одержимо відповідно вектори . Ці вектори й утворюють базис простору L розв’язків однорідної системи лінійних рівнянь.

6.Загальний розв’язок лінійної системи однорідних рівнянь у цьому випадку є лінійною комбінацією базисних векторів:

.

Неоднорідні системи. Теорема Кронекера – Капеллі: система неоднорідних лінійних рівнянь Ах = b сумісна тоді і тільки тоді, коли rangА = rang.

При цьому якщо rangА = rang= n, то система має єдиний розв’язок і він може бути знайдений за правилом Крамера.

Якщо rangА = rang < n, то система має нескінченно багато розв’язків, які утворюють лінійний многовид. При цьому підпростір зсуву – це простір L розв’язків однорідної системи рівнянь, і його базис можна побудувати способом, який було розглянуто вище. Вектор зсуву – це частинний розв’язок неоднорідної системи рівнянь. і він може бути знайдений, якщо в неоднорідній системі вільні невідомі покласти рівними деяким довільним значенням (наприклад, нульовим).

Загальний розв’язок неоднорідної системи – це загальний розв’язок відповідної однорідної системи плюс деякий частинний розв’язок неоднорідної системи. Останнє твердження можна записати через абревіатури відповідних термінів: З.Р.Н.С. = З.Р.О.С. + Ч.Р.Н.С.

Обернена матриця. Запишемо систему в матричному вигляді Ах = b. Якщо detА ¹ 0 (така матриця А називається невиродженою), то для матриці А існує матриця А–1 така, що А–1А = АА–1 = Е. Така матриця називається оберненою до матриці А, і розв’язок системи можна записати за допомогою оберненої матриці у вигляді: А–1Ах = А–1b Þ х = А–1b.

Таким чином, у випадку існування оберненої матриці А–1 розв’язок системи має вигляд: х = А–1b.

Як же знайти обернену матрицю А–1 до невиродженої матриці А?

I спосіб.

1)  Складемо матрицю Аik з алгебраїчних доповнень до елементів аik матриці А;

2)  транспонуємо матрицю з алгебраїчних доповнень;

3)  кожен елемент матриці, що утворилась, ділимо на detА.

В результаті маємо обернену матрицю – А-1.

II спосіб.

1)  Запишемо матрицю А, а праворуч від неї, через вертикальну риску, –одиничну матрицю Е. Одержимо матрицю яка має n рядків та 2n стовпців;

2)  у матриці, що утворилась, за допомогою застосування до рядків (і тільки до рядків) перетворень, що не змінюють ранг матриці, утворимо на місці матриці А одиничну матрицю.

На місці одиничної матриці тепер стоїть А–1.

III спосіб. Праворуч від матриці припишемо одиничну матрицю Е, а знизу припишемо матрицю (–Е). У правому нижньому куті поставимо нульову матрицю. Використовуючи операції тільки над рядками матриці, що утворилась, на місці матриці (–Е) утворимо нульову матрицю. Тоді у правому нижньому куті буде стояти А–1.

IV спосіб. Для обернення матриці, що має блокову структуру, тобто матриці вигляду: , де А – квадратна матриця порядку n ´ n, а D – квадратна матриця q ´ q, справедливі дві формули Фробеніуса:

1.Перша формула Фробеніуса (якщо detА ¹ 0):

, де H = D – CA–1B.

2.Друга формула Фробеніуса (якщо detD ¹ 0):

, де K = A – BD–1C.

2. Контрольні питання і завдання

1.  Що таке ранг матриці і її базисний мінор? Чи визначаються вони однозначно?

1.2.  Знайти ранг і всі базисні мінори матриці: .

1.3.  Як пов'язані ранг матриці і вимірність лінійної оболонки її рядків.

1.4.  Чому дорівнює вимірність простору розв’язків однорідної системи лінійних рівнянь, якщо в системі 10 рівнянь, 16 невідомих і ранг матриці системи дорівнює 6?

1.5.  Чи утворює множина розв’язків неоднорідної системи лінійний простір? Яка з властивостей лінійного простору не виконується?

1.6.  Згадайте визначення лінійного многовиду. Що називається його базисом і вимірністю?

1.7.  Як визначається вектор зсуву для лінійного многовиду, що є множиною розв’язків неоднорідної системи?

3. Приклади розв’язування задач

Задача 1. Знайти ранг матриці .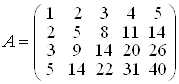

Розв’язання. Насамперед відзначимо, що четвертий рядок матриці є сумою другого і третього рядків і тому при вилученні цього рядка ранг матриці не зміниться.

1.Відкинемо четвертий рядок.

2.З другого і третього рядків матриці віднімемо перший рядок, помножений, відповідно, на 2 та 3.

3.В отриманій матриці з третього рядка віднімемо другий, помножений на 2.

Одержимо ланцюжок перетворень:

лінійний рівняння матриця

.

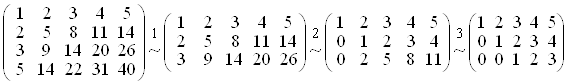У матриці, що утворилась, мінор, який стоїть в перших трьох стовпцях, не дорівнює нулю. Отже, ранг вихідної матриці дорівнює 3 і мінор 3-го порядку, що стоїть в перших трьох стовпцях, є базисним мінором матриці А.

Задача 2. Знайти матрицю, яка є оберненою до матриці

.

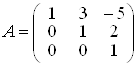Розв’язання. Знайдемо обернену матрицю за визначенням. Нехай обернена матриця має вигляд: . Тоді, за визначенням,

АА–1 = Е, тобто .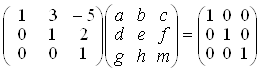

Знаходячи добуток матриць, одержимо рівності:

.

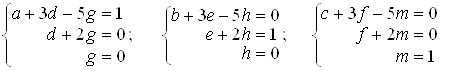Із цих співвідношень одержуємо: g = 0, d = 0, a = 1; далі: h = 0, e =1, b = –3. І нарешті: m = 1, f = –2, c = 11. У підсумку дійдемо висновку, що:

.

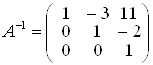Задача 3. Знайти матрицю, яка є оберненою до матриці .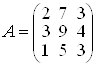

Розв’язання. Побудуємо матрицю 6 ´ 6, дописавши праворуч від А одиничну матрицю Е, внизу матрицю (– Е), а інші місця заповнимо нулями.

.

За допомогою операцій над рядками матриці А¢ утворимо на місці (–Е) нульову матрицю. Тоді в правому нижньому куті буде стояти матриця А–1.

1.До всіх рядків матриці А¢ додамо третій рядок з деяким множником, домагаючись того, щоб всі елементи першого стовпця, крім а31, дорівнювали нулю.

2.Перший рядок отриманої матриці поділимо на (–3) і, додаючи до інших рядків матриці отриманий перший рядок з деякими множниками, досягаємо того, щоб у другому стовпці стояли нулі, крім елемента а12.

3.За допомогою другого рядка утворимо нулі в третьому стовпці, крім елемента а23.

Одержимо ланцюжок перетворень:

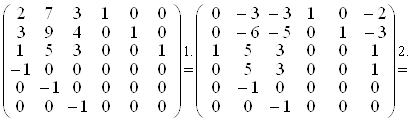
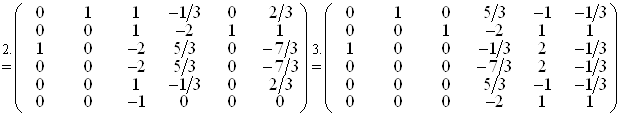
Звідси укладаємо, що .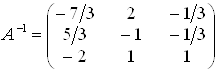

Задача 4. Знайти матрицю, яка є оберненою до .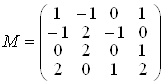

Розв’язання. Для обернення матриці застосуємо першу формулу Фробеніуса. Позначимо: , , , .

Знаходимо послідовно:

;

;

;

.

І тоді 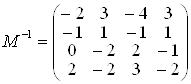. Привабливість зазначеного способу полягає в тому, що для обернення матриці 4-го порядку ми маємо справу з оберненням матриць лише 2-го порядку, що істотно простіше.

Задача 5. За допомогою правила Крамера розв’язати систему лінійних неоднорідних рівнянь: .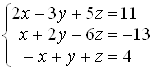

Розв’язання. Головна матриця системи має вигляд: .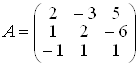

Розв’язок системи може бути знайдений за правилом Крамера, тому що detА = D = 18 ¹ 0. Для цього побудуємо визначники Dх, Dу, Dz, які відрізняються від головного визначника тим, що в ньому стовпець коефіцієнтів при, відповідно, х, у та z замінено на стовпець вільних членів, тобто:

.

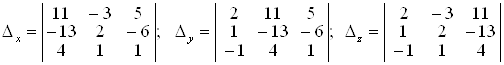Обчислюючи їх, знаходимо, що Dх = 18, Dу = 36, Dz = 54.

Отже .

Задача 6. Розв’язати систему лінійних однорідних рівнянь:

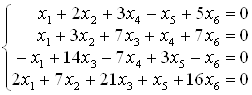
Розв’язання. Насамперед відзначимо, що система напевне сумісна, оскільки однорідна система завжди має щонайменше нульовий розв’язок.

Почнемо пошук загального розв’язку даної системи. Головна матриця системи має вигляд: .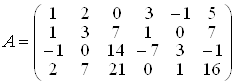

Знайдемо ранг матриці А. Перший рядок матриці з відповідними множниками додамо до інших рядків матриці так, щоб елементи першого стовпця обернулися на нуль, крім елемента а11. Вийде матриця А1 така, що

rangА1 = rangА і .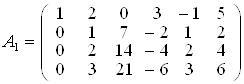

Відзначаючи, що третій і четвертий рядки матриці пропорційні другому рядку, укладаємо, що rangА1 = rangА2, де . Помножимо другий рядок матриці А2 на (–2) і додамо до першого рядка. Одержимо матрицю А3: , таку, що rangА3 = rangА2 = 2. У підсумку rangА = rangА3 = 2.

Тоді вийшла система двох рівнянь, з яких можна написати:

х1 = 14х3 – 7х4 + 3х5 – х6, х2 = –7х3 + 2х4 – х5 – 2х6 і змінні х3, х4, х5, х6 – будь-які. Це і є розв’язок системи.

Однак можна (і необхідно) піти далі. Множина розв’язків лінійної однорідної системи утворює лінійний простір L вимірності dimL = n – rangА = 6 – 2 = 4. Для знаходження базисних векторів простору розв’язків надамо вільним невідомим х3, х4, х5, х6 значення: а) 1, 0, 0, 0; б) 0, 1, 0, 0; в) 0, 0, 1, 0; г) 0, 0, 0, 1. Одержимо чотири вектори, що утворять базис L: е1 = (14, –7, 1, 0, 0, 0); е2 = (–7, 2, 0, 1, 0, 0); е3 = (3, –1, 0, 0, 1, 0); е4 = (–1, –2, 0, 0, 0, 1). У такий спосіб L = ℒ(е1, е2, е3, е4), і будь-який розв’язок вихідної системи може бути записаний у вигляді лінійної комбінації базисних векторів, тобто у вигляді: с1(14, –7, 1, 0, 0, 0) + с2(–7, 2, 0, 1, 0, 0) + с3(3, –1, 0, 0, 1, 0) + с4(–1, –2, 0, 0, 0, 1), де с1, с2, с3, с4 – будь-які значення. Це і є загальний розв’язок вихідної лінійної однорідної системи рівнянь.

Задача 7. Розв’язати систему лінійних неоднорідних рівнянь

Розв’язання. Розширена матриця системи рівнянь має вигляд: 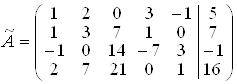, причому до вертикальної риски записана головна матриця системи, а після вертикальної риски – стовпець вільних членів. Перетворюючи матрицю  аналогічно до того, як перетворювалася матриця А в розв’язку попередньої задачі, одержимо матрицю А таку, що rang = rangА = 2 і . Звідси можна записати загальний розв’язок системи у вигляді: х1 = 1 + 14х3 – 7х4 – 3х5, х2 = 2 – 7х3 + 2х4 – х5, де х3, х4, х5 – будь-які.

Це і є загальний розв’язок вихідної системи лінійних рівнянь. Однак з метою прояснення алгебраїчної структури розв’язку системи відзначимо таке:

Враховуючи, що rang = rang A = 2 < n = 5, можемо зазначити, що множина розв’язків системи являє собою лінійний многовид. Вектором зсуву цього лінійного многовиду є частинний розв’язок неоднорідної системи рівнянь, для знаходження якого дамо вільним невідомим х3, х4, х5 довільні значення (наприклад нулі) і одержимо: f = (1, 2, 0, 0, 0). Підпростором зсуву є простір розв’язків однорідної системи з матрицею А2, яка збігається з головною матрицею вихідної системи неоднорідних рівнянь

 .

Звідси х1 = 14х3 – 7х4 – 3х5, х2 = – 7х3 + 2х4 – х5, де х3, х4, х5 – будь-які. Даючи вільним змінним х3, х4, х5 значення: а) 1, 0, 0; б) 0,1,0; в) 0, 0, 1; одержимо, відповідно, базисні вектори простору L розв’язків однорідної системи рівнянь: е1 = (14, –7, 1, 0, 0), е2 = (–7, 2, 0, 1, 0), е3 = (–3, –1, 0, 0, 1).

Отже, розв’язки вихідної системи утворюють лінійний многовид М:

M = {x ½x = f + c1e1 + c2e2 + c3e3}, де c1, c2, c3 – будь-які,