Контрольная работа: Теория вероятностей

Министерство образования и науки Российской Федерации

Бузулукский гуманитарно-технологический институт (филиал) государственного образовательного учреждения высшего профессионального образования

«Оренбургский государственный университет»

Факультет заочного обучения

Кафедра физики, информатики, математики

Контрольная работа

по дисциплине Математика

Руководитель работы:

Шабалина Л.Г.

Исполнитель:

Студент з-09 ПГС группы

Сушков Е.А.

Бузулук 2010

Задание 1

1. Рабочий обслуживает три станка, работающих независимо друг от друга. Вероятность того, что в течение часа 1-й станок не потребует внимания рабочего, равна 0,9; для второго - 0,8; для третьего – 0,85.

Какова вероятность того, что в течение часа:

а) ни один станок не потребует внимания рабочего;

б) все три станка потребуют внимания рабочего;

в) какой-нибудь один станок потребует внимания рабочего;

г) хотя бы один станок потребует внимания рабочего?

Решение: I II III

P 0, 9 0, 8 0, 85

а) А (i =1,2,3) – не потребует внимания станок в течение часа

В – событие, где все 3 станка не потребуют внимания рабочего в течение часа

Р (В) = Р (А1 × А2 × А3) = Р(А1) × Р(А2) × Р(А3) = 0,9 × 0,8 × 0,85 = 0,612

б) А (i =1,2,3) – не потребует i-й внимания станок

Ᾱ (i =1,2,3) – потребует i-й внимания станок, независимое событие

Р (Ᾱ 1) = 1 – 0,9 = 0,1

Р (Ᾱ 2) = 1 – 0,8 = 0,2

Р (Ᾱ 3) = 1 – 0,85 = 0,15

Р (Ᾱ 1 × Ᾱ 2 × Ᾱ 3) = (0,1 × 0,2 × 0,15) = 0,003

в) Ᾱ 1 = 0,1; Ᾱ 2 = 0,2; Ᾱ 3 = 0,85

Аi – один станок потребует внимания рабочего в течение часа

Р (В) = Р (А1 × Ᾱ 2 × А3 + Ᾱ 1 × А2 × А3 + А1 × А2 × Ᾱ 3) = (0,9× 0,2 × 0,85 + 0,1 × 0,8 × 0,85 + 0,9 × 0,8 × 0,15) = 0,329

г) Найдём вероятность через противоположное событие, т.е. ни один станок не потребует внимания рабочего в течение часа

Р (А1 × А2 × А3) = Р (А1) × Р (А2) × Р (А3) = 0,9 × 0,8 × 0,85 = 0,612

Р ( С) = 1 – 0,612 = 0,388

Ответ: а) вероятность равна 0,612, что в течение часа ни один станок не потребует внимания рабочего; б) вероятность равна 0,003, что в течение часа все три станка потребуют внимания рабочего; в) вероятность равна 0,329, что в течение часа какой-нибудь один станок потребует внимания рабочего; г) вероятность равна 0,388, что в течение часа хотя бы один станок потребует внимания рабочего.

Задание 2

Ящик содержит 10 деталей, среди которых 3 стандартные. Найти вероятность того, что среди отобранных 5 деталей окажутся: а) только 2 стандартные детали; б) все детали нестандартные; в) все детали стандартные; г) хотя бы одна деталь стандартная.

Решение:

а) число способов, где взяли 5 деталей из 10 детали, можно подсчитать по формуле:

С2 – число способов, где взяли 2 стандартные детали из 3-х нестандартных

С3 – число способов, где взяли 3 стандартные детали из 7-ми нестандартных

С5 – всего способов, где взяли 5 стандартных деталей из 10-ти

С2 =__3!___ = 3 С3 = __7!___ = 35 С5 = __10!___ = 252

2! × 1! 3! × 4! 5! × 5!

С3 × С7 = 3 × 35 = 0,417

С5 252

б) С7 – число способов выбора, где взяли 5 деталей из 7-ми

С5 = __7!__ = 21

5! × 2!

Число выбора деталей считается в сочетании С5 = 1

С7 – число способов, где взяли 5 деталей из 7-ми

С10 – всего способов, где взяли 5 деталей из 10-ти

Искомая вероятность Р ( Д):

Р (Д) = С7 × С3 = 21 × 1 = 0,083

С10 252

в) Событие, где взяли 5 стандартных деталей из 3-х стандартных деталей невозможно. Вероятность равна нулю.

г) Найдём искомую вероятность через противоположное событие:

С7 – число способов, где взяли 5 нестандартных деталей из 7-ми

С3 – число способов выбора из 3-х

С10 – всего способов, где взяли 5 деталей из 10-ти

С7 × С3 = 0,083 - искомая вероятность равна результату под пунктом б). С10

Ответ: а) Если среди отобранных 5 деталей окажутся только 2 стандартные детали, то вероятность равна 0,417; б) если среди отобранных 5 деталей окажутся все детали нестандартные, то вероятность равна 0,083; в) если среди отобранных 5 деталей окажутся все детали стандартные, то вероятность равна 0; г) если среди отобранных 5 деталей окажется, хотя бы одна деталь стандартная, то вероятность равна 0,083.

Задание 3

Имеется 2 ящика изделий, причем в одном ящике все изделия доброкачественны, а во втором - только половина. Изделие, взятое наудачу из выбранного ящика, оказалось доброкачественным. На сколько отличаются вероятности того, что изделие принадлежит первому и второму ящику, если количество изделий в ящиках одинаково?

Решение: I ящик II ящик

Доброкачественные 50 × 50 изделия Н1 – взяли из I ящика с доброкачественными изделиями, то Р ( Н1) = 0,5

Н2 – взяли из II ящика, то Р ( Н2) = 0,5

Событие А, где взяли доброкачественную деталь, Р ( А ǀ Н1) = 1

Событие А ǀ Н1 – доброкачественная деталь из I ящика

Событие А ǀ Н2 – из II ящика, Р ( А ǀ Н2) = 0,5

Тогда искомая вероятность Р ( А ) =Р ( Н1 ) × Р ( А ǀ Н1 ) + Р ( Н2 ) × Р (А ǀ Н2)

Р ( А) = 0,5 × 1 + 0,5 × 0,5 = 0,5 + 0,25 = 0,75

Р ( Н1 ) × Р ( А ǀ Н1 ) ˃ Р ( Н2 ) × Р ( А ǀ Н2)

Ответ: Если изделие принадлежит первому и второму ящику, и количество изделий в ящиках одинаково, то вероятности отличаются на 0,75.

Задание 4

В ящике находятся изделия, сделанные на трех станках: 20 – на первом станке, 18 - на втором и 14 - на третьем. Вероятности того, что изделия, изготовленные на первом, втором и третьем станках, отличного качества, соответственно, равны 0,7; 0,85; 0,9. Взятое наудачу изделие оказалось отличного качества. Какова вероятность того, что оно изготовлено на втором станке?

Решение: I II III

20 18 14

0,7 0,85 0,9

Р ( А ǀ Н1 ) = 0,7 Р ( А ǀ Н2 ) = 0,85 Р ( А ǀ Н3 ) = 0,9

Р ( А) = 0,7 × 0,85 × 0,9 = 0,536

А – взятое изделие отличного качества из II станка

Искомая вероятность равна:

Р ( Н2 ǀ А ) = ________ Р ( Н2 ) × Р ( А ǀ Н2)

Р ( Н1 ) × Р ( А ǀ Н1 ) + Р ( Н2 ) × Р ( А ǀ Н2 ) + Р ( А ǀ Н3)

Где Н1, Н2, Н3 – соответственно изготовлено изделий на станках I, II и III.

Р ( А ǀ Н1) = 0,7 – вероятность отличной детали I станка

Р ( А ǀ Н2) = 0,85 – вероятность отличной детали II станка

Р ( А ǀ Н3) = 0,9 – вероятность отличной детали III станка

Р ( Н2 ǀ А) = ________ 0,346 × 0,85 ______________ = 0,294 = 0,365

0,385 × 0,7 + 0,346 × 0,85 + 0,269 × 0,9 0,806

Ответ: Вероятность равна 0,365, что взятое наудачу изделие оказалось отличного качества изготовлено на втором станке.

Задание 5

Найти вероятность того, что событие А произойдет не менее 2 раз в 4 независимых испытаниях, если вероятность наступления события А в одном испытании равна 0,6.

Решение:

Событие А произойдёт не менее 2-х раз в 4 независимых испытаниях

Р ( А ) = р Р ( А) = Сm × рm × qn - m

Р = 0,6

q = 1 – р = 1 – 0,6 = 0,4

– вероятность противоположного события. Нет наступления события А в 1-ом испытании.

Найдём произведение npq и определим формулу вычисления:

вероятность случайный величина интегральный

n = 4 npq = 4 × 0,6 × 0,4 = 0,96

Можно использовать формулу Бернули:

Р ( А) = С2 × p2 × q2 + С3 × р3 × q1 + С4 × р4 × q0

Найдём через противоположное событие:

Р ( А) = 1 – С0 × p0 × q4 + С1 × p1 × q3 = 1 – 1 × 1 × (0,4)4 + 4 × 0,6 × (0,4)3 = 1 – 0,0256 + 4 × 0,6 × 0,064 = 0,9744 + 0,1536 = 1,128

С4 = __4!__ = 4

1! × 3!

Ответ: Если событие А произойдет не менее 2 раз в 4 независимых испытаниях, то вероятность равна 1,128.

Задание 6

Вероятность того, что пара обуви, наудачу из изготовленной партии, окажется 1-го сорта, равна 0,7. Определить вероятность того, что из 2100 пар, поступающих на контроль, число пар первосортной обуви окажется не менее 1000 и не более 1500.

Решение:

Для решения задачи используем интегральную формулу Муавра – Лапласа.

Вероятность событий Рn (m1 ˂ m ˂ m2) = Ф (х2) – Ф (х1)

р = 0,7; n = 2100; m1 = 1000; m2 = 1500; q = 0,3

х1 = _m1 – np_ = 1000 – 2100 × 0,7 = 1000 – 1470 = – 470 = – 22,38

√ npq √2100 × 0,7 × 0,3 √441 21

х2 = _m2 – np_ = 1500 – 2100 × 0,7 = 1500 – 1470 = _30_ = 1,43

√ npq √2100 × 0,7 × 0,3 √441 21

Ф ( – х) = – Ф (х) Ф (– 22,38) = 0,5 Ф (– 22,38) = 0,4236

Ф (х2) – Ф (х1) = Ф (х2) + Ф (х1) = 0,5 + 0,4236 = 0,9236

Ответ: Если число пар первосортной обуви окажется не менее 1000 и не более 1500, то из 2100 пар, поступающих на контроль, равна вероятности 0,9236.

Задание 7

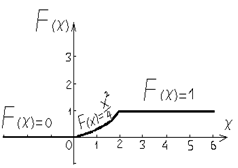
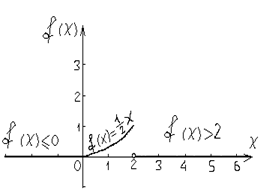
Случайная величина Х задана интегральной функцией F(x). Требуется: а) найти дифференциальную функцию f(х) (плотность вероятности), б) найти математическое ожидание и дисперсию Х, в) построить графики интегральной и дифференциальной функций, г) вероятность попадания случайной величины Х в интервал .

Решение:

По определению Fʹ (х) = f (х)

0, при х ≤ 0

f ( х) = х2 , при 0 ˂ х ≤ 2

1, при х ˃ 2

Fʹ ( х ) = 0ʹ = 0 Fʹ ( х ) = ( х2 ÷ 4 )ʹ = 0,5х Fʹ ( х ) = 1ʹ = 0

в) Построение графиков интегральной и дифференциальной функции.

б) М (Х) = х f (х) dx = 0 dx + х × _1_ dx + 0 dx =_ 1_ × х3 ÷ 3 = х3 ÷ 6 =

2 2 =_ 23_ – _03 = 8 – 0 = 4 = а

6 6 6 3

Д (Х) = (х – _4_)2 f (х) dx = 0 (х – _4)2 f (х) dx + (х – 4)2 1 х dx +

3 3 3 2

+ (х – 4_)2 f (х) dx = (1 х3 – 4 х2 + 8 х) dx = (1_× х4 - 4_× х3 + 8_× х2) =

3 2 3 9 2 3 9

= 1_ × 24 – 4 × 23 + 8_ × 22 = 16 – 32 + 16 = 144 – 128 = 16 = _2_

2 4 3 3 9 2 8 9 9 72 72 9

г) Р ( 1 ˂ Х ˂ 2) = F (в) – F (а) 22 × 1 – 12 × 1 = _1 – _1 = _1_ ––

3 4 3 4 9 12 12

вероятность попадания в этот промежуток.

Ответ: М (Х) = _4 = а ; Д (Х) = _2 ; Р ( 1 ˂ Х ˂ 2) =_ 1_

3 9 12

Задание 8

Найти вероятность попадания в заданный интервал ( a,b ) нормально распределенной случайной величины Х, если известны ее математическое ожидание а и среднее квадратическое отклонение s.

a = 2, b = 13, а = 10, s = 4.

Решение:

Если случайная величина Х нормально распределена, то она является непрерывной случайной величиной, и М (Х) вычисляется, как: (a + b) ÷ 2, а Д (Х) вычисляется, как: (b-a) ÷ (в-а), и s связаны формулой √ Д.

Тогда вероятность: Р { Х ϵ [a,b] } будет вычисляться по формуле:

Ф ( ( b – a ) ÷ s) – Ф ( (a – b) ÷ s ).

М (Х) = (a + b) ÷ 2 = (2 + 13) ÷ 2 = 7,5

Д (Х) = (b - a)2 ÷ 12 = 9 ÷ 12 = 0,75

s = √ Д = √ 0,75 = 0,87 × 100 = 87

То искомая вероятность находится по формуле:

Р (a ˂ Х ˂ b ) = Ф ( ( b – a ) ÷ s ) – Ф ( (a – b) ÷ s ) = Ф ((13 – 10) ÷ 4) –

Ф ((2 – 10) ÷ 4) = Ф (0,75) – Ф (– 2) = Ф (0,75) + Ф (2) = 0,2734 + 0,5 =

=0,773

Где Фх – функция Лапласа, которую находим по таблице.

Ответ: Вероятность попадания в заданный интервал ( a,b ) нормально распределенной случайной величины Х, равна 0,773.

Задание 9

Найти доверительные интервалы для оценки математического ожидания нормального распределения с надежностью 0,95, если выборочная средняя , объем выборки n и среднее квадратическое отклонение s.

= 12, 15, n = 169 s = 5

Решение:

Находим доверительные интервалы: х – t γ ˂ а ˂ х + t γ

√ n √ n

где Ф (t) = Ф (γ ÷ s) → t = (γ ÷ s) = (0,95 ÷ 5) = 0,19

х – t γ = 12,15 – 0,19 × 0,95 = 12,15 – 0,01 = 12,14

√ n √ 169

х + t γ = 12,15 + 0,19 × 0,95 = 12,15 + 0,01 = 12,16

√ n √ 169

Ответ: Доверительные интервалы 12,14 ˂ а ˂ 12,16.

Литература

1. Севастьянов Б.А., Чистяков В.П, Зубков А.М. Сборник задач по теории вероятностей – М.: Наука, 1980.

2. Шипачев В.С. Высшая математика. М.: Высшая школа, 2004.

3. Чистяков В.П. Курс теории вероятности, М.: 2001.

4. Гмурман В.Е. Теория вероятностей и математическая статистика.- М.: Высшая школа, 2003.

5. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике.- М.: Высшая школа, 2003.

6. Данко П.Е и др. Высшая математика в упражнениях и задачах (I и II часть).-М, 2005.

7. Богаров П.П., Печинкин А.В. Теория вероятностей. Математическая статистика – М.: 1998.

8. Венцель Е.С. Теория вероятностей – М.: 1962.

9. Солодовников А.С. Теория вероятностей М.: Просвещение, 1978.

10. Виленкин Н.Я., Потапов В.Т. Задачник-практикум по теории вероятности с элементами комбинаторики и математической статистики.

11. Кремер Н.Ш.: «Теория вероятностей и математическая статистика»; М.ЮНИТИ – Дана, 2003.