Лабораторная работа: Представлення і перетворення фігур

Лабораторная работа: Представлення і перетворення фігур

ПРЕДСТАВЛЕННЯ І ПЕРЕТВОРЕННЯ ТОЧОК

Представлення точок здійснюється наступним чином:

На площині

У просторі

Перетворення точок.

Розглянемо результати матричного множення , що визначає точку Р, і матриці перетворення 2х2 загального виду:

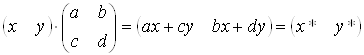                     (3.1)

Дослідимо декілька часткових випадків.

1) а=d=1 і c=b=0. Змін не відбувається

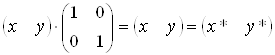.                            (3.2)

2) d=1, b=c=0. Зміна масштабу по осі x

.                           (3.3)

3) b=c=0. Зміна масштабу по осях x і y

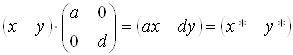.                         (3.4)

4) b=c=0, d=1, a=-1. Відображення координат відносно осі y

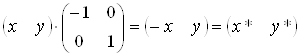.                       (3.5)

5) b=c=0, a=d<0. Відображення відносно початку координат

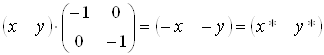.                            (3.6)

6) а=d=1,c=0. Зсув

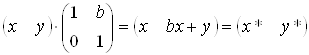.                      (3.7)

Для початку координат маємо інваріантно

.

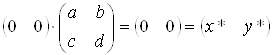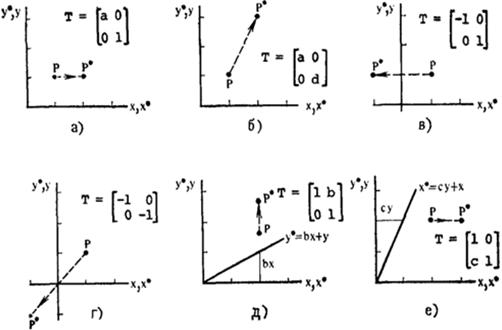
Рис.3.1. Перетворення точок.

ПЕРЕТВОРЕННЯ ПРЯМИХ ЛІНІЙ

Пряма задана 2 векторами.

Вектори положення точок А і В рівні  і .

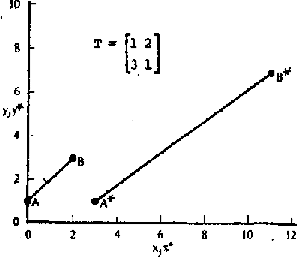
Рис.3.2. Перетворення прямих ліній.

Матриця перетворення

.

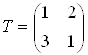Одержимо:

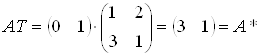,                                (3.8)

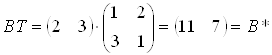.                             (3.9)

Альтернативне представлення лінії AB

.

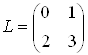Після цього множення матриці L на Т дасть

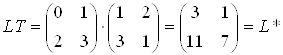.                                    (3.10)

Операція зсуву збільшила довжину лінії і змінила її положення.

ОБЕРТАННЯ

Розглянемо плоский трикутник ABC.

Здійснимо поворот на 90° проти годинникової стрілки.

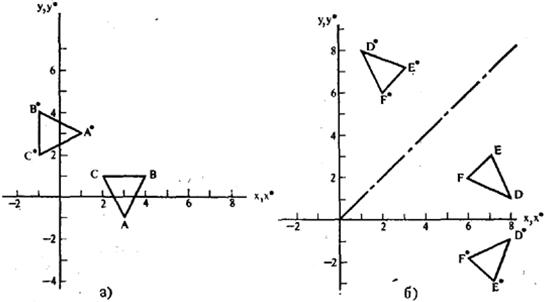
Рис.3.3. Обертання і відображення.

Одержимо

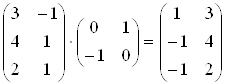.                             (3.11)

В результаті отримаємо трикутник A*B*C*. Поворот на 180° задається матрицею

,

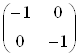поворот на 270° навколо початку координат - за допомогою матриці:

.

ВІДОБРАЖЕННЯ

Відображення визначається поворотом на 180° навколо осі, що лежить у площині ху.

1) Обертання навколо прямої y=x задається матрицею:

.

Нові вирази визначаються співвідношенням:

.                                   (3.12)

2) Обертання навколо осі y=0 задається матрицею:

.

Нові вершини визначаються співвідношенням:

.                              (3.13)

ЗМІНА МАСШТАБУ

Зміна масштабу визначається значенням 2-х елементів головної діагоналі матриці.

Якщо використовуємо матрицю 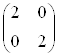 маємо збільшення в 2 рази.

Якщо значення елементів не рівні, то має місце спотворення.

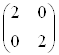Трикутник ABC перетворений за допомогою матриці . Трикутник DEF перетворений за допомогою матриці 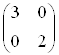. Маємо спотворення.

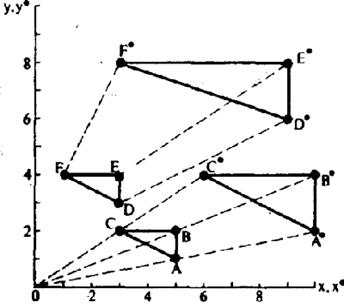
Рис.3.4. Рівномірна і нерівномірна зміна масштабів.

ДВОВИМІРНИЙ ЗСУВ І ОДНОРІДНІ КООРДИНАТИ

Введемо третій компонент у вектори точок  і - і .

Матриця перетворення матиме вигляд:

перетворення фігура площина точка

.

Таким чином,

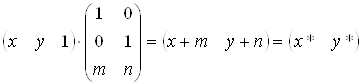.           (3.14)

Константи m, n викликають зсув x* і y* відносно x і y.

Матриця 3х2 не квадратна - вона не має оберненої матриці.

Доповнимо матрицю перетворення до квадратної

.                                                        (3.15)

Третій компонент не змінюється.