
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по муниципальному праву
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Реферат: Возможности анализа данных медико-биологических экспериментов в программе Statistica
Реферат: Возможности анализа данных медико-биологических экспериментов в программе Statistica
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования «Международный государственный экологический университет имени А.Д. Сахарова»
Реферат
на тему
«Возможности анализа данных медико-биологических экспериментов в программе Statistica»
Магистрант кафедры иммунологии
Петрова Елена Александровна
Научный руководитель: к. м. н.,
доцент Зафранская Марина Михайловна
Минск 2011
Введение
Статистика в медико-биологическом исследовании
Выбор метода анализа в соответствии с типом распределения данных
Анализ времени жизни в ППО Statistica
Сравнение коэффициентов корреляции
Практическая часть
Заключение
Литература
Развитие медицины невозможно без проведения медико-биологических экспериментов, эпидемиологического анализа, оценки эффективности фармакологических препаратов и других исследований как доклинического, так и клинического уровня.
Объектом научного исследования обычно выступает не просто отдельное явление, конкретная ситуация, а целый класс сходных явлений и ситуаций, их совокупность. Цель и непосредственные задачи научного исследования состоят в том, чтобы найти общее у ряда единичных явлений, выявить законы, по которым они возникают, развиваются и функционируют [1, 2, 3 ]. Важнейшим обстоятельством, определившим необходимость применения математико-статистических методов, явилось установление факта, что многим биологическим системам свойственны статистические закономерности, обнаруживаемые при изучении совокупностей, но неприменимые к отдельным единицам этих совокупностей [2].
Отличительными признаками научного исследования являются:
1. целенаправленность процесса (достижение поставленной цели, выполнение четко сформулированных задач)
2. направленность на поиск, на творчество, на выдвижение идей
3. систематичность как самого процесса исследования, так и его результатов
4. строгая доказательность, обоснованность выводов [4, 5, 6]
Развитие идей критической оценки медицинской информации привело к возникновению в конце 80-х годов XX века концепции доказательной медицины (ДМ).
Основными постулатами ДМ являются следующие [7]:
— каждое решение врача должно основываться на научных данных;
— вес каждого факта тем больше, чем строже методика научного исследования, в ходе которого он получен.
ДМ является концепцией как для врачей, исследователей, руководителей учреждений и органов здравоохранения, так и для пациентов. Основная цель концепции ДМ состоит в том, чтобы постепенно превратить врачебную деятельность из искусства в науку [7].
Любое исследование в зависимости от того, насколько надежны полученные в нем результаты и насколько они применимы в клинической практике, можно охарактеризовать с двух точек зрения:
— достоверности (внутренней обоснованности)
— о6общаемости (внешней обоснованности, применимости)
Достоверность (внутренняя обоснованность) исследования определяется тем, в какой степени структура исследования соответствует поставленным задачам, а полученные результаты справедливы в отношении изучавшейся выборки.
Обобщаемость (внешняя обоснованность) результатов исследования отражает, в какой мере результаты данного исследования применимы к другим группам, например к больным другого пола, другой популяции и т.п.
Достоверность и о6общаемость зависят от правильности проведения исследования на всех этапах, в том числе, от грамотной статистической обработки полученных данных [7].
Широкая доступность вычислительной техники дает возможность обработки больших объемов данных, использования различных методов анализа. Кроме того, программа конкретного метода обработки позволяет многократно повторять вычисления с небольшими изменениями без дополнительных усилий. Для большинства стандартных статистических методов существуют пакеты программ, хотя им порой не хватает гибкости, которую в идеале они должны были бы допускать. Для большинства задач с небольшими объемами данных и с относительно простыми методами обработки вполне достаточно обычного калькулятора. Для данных среднего объема лучше пользоваться пакетами стандартных программ. Однако следует избегать использования сложных методов анализа только потому, что имеются соответствующие программы [6].
На сегодняшний день лидером среди программ статистической обработки данных в среде Windows является пакет программного обеспечения (ППО) STATISTICA, который имеет более 250 тыс. зарегистрированных пользователей во всем мире и является наиболее динамично развивающимся пакетом на рынке статистического программного обеспечения. Разработчиком STATISTICA является фирма StatSoft, Inc., (США). Первая версия системы STATISTICA для DOS, вышедшая в 1991 году, представляла собой новое направление развития статистического программного обеспечения. В ней реализован так называемый графически-ориентированный подход к анализу данных [5,6].
Однако при использовании ППО STATISTICA, как и при работе с любыми другими пакетами статистических программ, принятие решений остается за исследователем. Программа освобождает исследователя от рутинной вычислительной работы, но интерпретация полученных результатов зависит от его опыта и знаний.
Применение статистики в медицинских и биологических исследованиях не ограничивается анализом результатов. Статистические методы следует использовать также на этапе планирования биологического эксперимента или медицинского исследования. Следует подчеркнуть, что с точки зрения клинической эпидемиологии для получения надежных, научно обоснованных результатов необходимы 2 компонента:
· правильное планирование структуры исследования (обеспечивающей возможность получения ответов на поставленные вопросы)
· грамотный статистический анализ [6].
Статистика в медико-биологическом исследовании
statistica статистика медицинский биологический
Всякое исследование должно удовлетворить следующим требованиям:
1. целеустремленность (конкретность задач). При анализе полученных данных могут быть выявлены и дополнительные результаты, не запланированные в исследовании (вторичные данные), однако обычно они представляют меньшую ценность, чем основные (соответствующие поставленной цели) результаты проводимого эксперимента.
2. эффективность, т. е. полученные выводы должны быть достоверны. Достоверность медико-биологических экспериментов обычно оценивается 5% уровнем значимости, и полученные значения, вероятность ошибки 1 рода для которых менее 5 %, автоматически выделяются в STATISTICA красным цветом шрифта. Однако, величина р может составлять 0,049; такое различие статистически значимо, но настолько близко к пороговой величине (0,05), что практически не отличается от, к примеру, 0,051, т. е. статистически незначимого уровня. Наличие подобной условной черты (0,05) представляет собой одну из проблем при использовании величины р.
3. экономность (минимальная затрата сил и средств, риску подвержено минимальное количество участников (как людей, так и животных)). Экономность может быть достигнута подбором минимальной численности групп, достаточной для получения достоверных результатов [5, 6, 8, 10].
4. Полученная последовательность случайных чисел может использоваться разными способами:
5. — четные числа могут соответствовать одной группе, а нечетные — другой (в случае двух групп);
—при числах в диапазоне от 0 до 99, числа меньшие 50, могут соответствовать одной группе, а большие или равные 50 — другой (в случае двух групп);
В результате простой рандомизации группы могут значительно различаться по числу участников, причем различие оказывается весьма существенным, если выборки невелики по объему. В связи с этим простую рандомизацию рекомендуется использовать лишь в масштабных КИ [7].
| Формулирование целей |
| ↓ |
| Планирование |
| ↓ |
| Выполнение (сбор данных) |
| ↓ |
| Подготовка данных |
| ↓ |
| Анализ данных |
| ↓ |
| Интерпретация результатов |
| ↓ |
| Формулировка выводов |
| ↓ |
| Публикация |
Рис. 1—Этапы научного исследования [7].
ППО STATISTICA не имеет модуля для расчета объема выборок.
При подготовке результатов к анализу ввод может осуществляться как в файлы данных ППО STATISTICA (имеют формат *.stа), так и в таблицы пакета МS Ехсеl с последующим импортом в STATISTICA [7]. Данные следует располагать в строках и столбцах электронной таблицы. В строках располагаются наблюдения (объекты исследования), в столбцах — переменные (признаки). Качественные данные могут быть представлены текстовыми значениями, которые автоматически кодируются числовыми значениями, однако такое представление не рекомендуется из-за возрастания вероятности ошибок [7, 10].
Рекомендовано вносить в качестве исходных данных результаты эксперимента без предварительной обработки с необходимым уровнем точности [6].
Первым шагом, предваряющим статистический анализ данных, является анализ типов данных. Это необходимо делать для определения способа представления и статистического метода обработки данных. Не рекомендовано проведение таких предварительных расчетов как:
1. Предварительная разбивка области значении непрерывного количественного признака на интервалы. При этом во-первых происходит потеря информации, а во-вторых— возможности статистического пакета позволяют автоматически осуществить разбивку областей значений количественных признаков на интервалы.
2. Вычисление различных расчетных индексов (коэффициентов, отношений и т.п.). Эти вычисления с большей точностью также могут быть проведены в STATISTICA.
Ошибки ввода (набора) можно выявить следующим способом—дважды щелкнув по имени столбца в открывшемся диалоговом окне выбрать Values/Stats. Ошибки (выпадающие значение) могут попасть в минимальные или максимальные, а ошибки типа двойной запятой—выносятся в правый столбец.
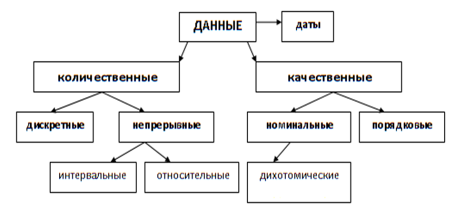
Рис.2—Типы данных [7].
STATISTICA позволяет работать со всеми типами данных. В большинстве модулей анализа ППО ограничивает тип вводимых данных в соответствии с применимостью того или иного метода. Так, при работе в модуле логистической регрессии могут быть использованы только бинарные данные (кодируются 0 и 1). Статистическую обработку данных удобно разбить на следующие четыре этапа.
1. Начальная обработка, т.е. представление исходных данных в подходящей для анализа форме, и проведение проверки качества данных.
2. Предварительный анализ данных, направленный на выяснение общей формы данных и предложение путей более обстоятельного анализа. Часто такой предварительный анализ успешно проводится простыми графическими методами или путем табличного представления данных.
3. Итоговый анализ (статистическая обработка), цель которого – дать основу для выводов.
4. Представление выводов в краткой и ясной форме. Обычно это приводит к необходимости интерпретации выводов на языке рассматриваемой области исследования [6].
Любой статистический анализ начинается с определения основных параметров описательной статистики, таких как мода, медиана, значения перцентилей и т. д. вычисление параметров описательной статистики осуществляется в модуле Basic Statistics/Tables (Основные статистики и таблицы).
В модуле Basic Statistics/Tables в разделе Summary.Descriptive на вкладке Advaced позволяет вычислить следующие параметры описательной статистики:
· Valid N — общее число вариантов в выборке;
· Mean — среднее арифметическое;
· Sum - сумма всех значений вари; Median — медиана;
· Standard Deviation - среднее квадратическое отклонение выборки;
· Variance — дисперсия выборки;
· Standard error of mean — ошибка среднего арифметического;
· 95% confidence limits of mean — 95% доверительный интервал для среднего;
· Minimum & maximum — минимум и максимум;
· Lower & upper quartiles — границы 1 и 3 квартилей;
· Range — размах выборки (определяется как разность между максимальным и минимальным значениями вариантов);
· Quartile range — диапазон квартилей;
· Skewness — коэффициент асимметрии
· Kurtosis — коэффициент эксцесса
· Standard error of skewness — стандартная ошибка асимметрии
· Standard error of kurtosis — стандартная ошибка эксцесса [7].
Выбор метода анализа в соответствии с типом распределения данныхСуществует множество методов статистического анализа данных. В каждом конкретном случае можно выбрать несколько возможных вариантов анализа. Однако при несоблюдении критериев использования того или иного метода полученный результат может оказаться неточным.
Наиболее характерными являются ошибки:
· использование параметрических методов (основанных на предположении о нормальном распределении данных) для анализа данных, не подчиняющихся нормальному распределению (1);
· использование методов, предназначенных для независимых выборок, при анализе парных данных (2) [10, 11].
STATISTICA позволяет проверить описываются ли распределение признаков нормальным законом распределения (з. Гаусса). В тех случаях, если данные распределяются по какому-либо иному закону, нельзя проводить сравнение по достаточно популярным критериям Стьюдента или подсчет корреляции по методу Пирсона. Если данные являются дискретными, их сопоставление проводится по критериям c2, а непрерывные данные сопоставляются по критерию Колмогорова — Смирнова. Рассчитать критерии Колмогорова — Смирнова для нормального расправления можно в модуле Basic Statistics/Tables (Descriptive Statistics--Normality --Kolmogorov-Smirnov & Lilliefors test for normality) с помощью Frequency tables либо Histograms.
В пакете STATISTICA можно сопоставить данные не только с нормальным, но и с некоторыми другими законами распределения c помощью Distributiom fitting (в меню Statistics). Если данные являются дискретными величинами, выбор распределения проводится в разделе Discrete Distributions, если же они являются непрерывными величинами — то в разделе Continuous Distributions. Несмотря на то что критерии Колмогорова—Смирнова и c2 достаточно четко позволяют ответить на вопрос, каким законом описываются полученные данные, их недостатком является то, что при малых значениях выборки достоверность оценки снижается.
При нормальном распределении данных коэффициент асимметрии должен быть равен нулю, а коэффициент эксцесса должен быть равен трем, что является ещё одним методом проверки типа распределения.
Для выявления взаимосвязи нескольких переменных, измеряемых по порядковой или интервальной шкале коэффициент корреляции Пирсона. Этот коэффициент, как и всякий параметрический показатель, весьма подвержен влиянию значений, резко отклоняющихся от среднего [9].
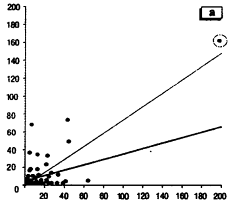
Рис.3 – Влияние выпадающего значения на линейное уравнение регрессии [9].
На рисунке проиллюстрирован случай, когда высокое значение коэффициента по Пирсону обусловленным единственной «выпадающей» точкой (выделена кружком). Показана линейная регрессия с учетом этого образца (тонкая верхняяя линия) и без него (толстая нижняя линия) [9].
Более рационально использование ранговых методов— вычисления коэффициента корреляции Кендалла (для порядковых переменных/шкал) или коэффициента корреляции Спирмена — непараметрического аналога коэффициента Пирсона для интервальных и порядковых переменных, не подчиняющихся нормальному распределению. Коэффициент Пирсона равен 1 (или минус 1) тогда и только тогда, когда две переменные (х и у) связаны линейной зависимостью (у=в+ах). Коэффициент Спирмена (или Кендалла) равен 1, если две переменные связаны правилом: большему значению переменной х всегда соответствует большее значение переменной у. Чем ниже коэффициент корреляции, тем сильнее отклонение от этих правил [9].
Следует помнить, что наличие корреляции двух переменных не означает их причинно-следственной связи [8].
Существуют следующие способы сравнения двух групп по количественным признакам: вычисление доверительного интервала для разности средних или проверка гипотез (параметрическими или непараметрическими методами). В случае соответствия нормальному закону распределения переменных в каждой группе сравнение групп проводится по критериям Стьюдента (статистический модуль Basic Statistics/Tables). В противном случае - использовать непараметрические критерии, которые находятся в модуле Nonparametrics [5].
При сравнении более двух групп по количественным признакам используют однофакторный дисперсионный анализ (параметрический или непараметрический) в случае независимых групп и непараметрический метод Фридмена в случае зависимых групп. Для сравнения групп по качественным признакам используют только непараметрические критерии.
Проблема ошибочного использования методов сравнения, предназначенных для несвязанных (независимых групп), к зависимым группам отчасти решается структурой таблиц данных (размещение результатов последовательных измерений (принадлежащих к зависимым группам) в строках, а независимых—в столбец в соответствии со столбцом, содержащим код группы (Indep. (grouping) variable)). Более того, в программе пиктограммы, сопровождающие названия методов анализа носят характер подсказки: показано взаимное расположение сравниваемых массивов данных (рис.4).

Рис. 4—Список инструментов анализа с пиктограммами в модуле непараметрических методов.
При интерпретации результатов при отсутствии достоверных различий ошибочным является заключение об их отсутствии, и может быть принято только заключение о том, что различия именно не были выявлены, хотя могут и присутствовать (характерно для выборок малой численности). С другой стороны, особенно на больших выборках могут быть выявлены различия, не имеющие биологического или медицинского значения. И наоборот, даже существенное различие, выявленное при сравнении небольших групп, имеющее клиническое значение, но не быть при этом статистически значимым. Если в ходе исследования, включающего несколько больных в терминальном состоянии, хотя бы один из участников в какой-либо из групп выживет, такой результат будет клинически значимым, хотя статистически значимое различие в частоте выживания между группами может отсутствовать [11].
При проведении анализа данных часто возникает так называемая проблема множественных сравнений (ПМС), заключающаяся в следующем: чем больше статистических гипотез проверяется на одних и тех же данных, тем более вероятна ошибка первого рода — заключение о наличии различий между группами, в то время как на самом деле верна нулевая гипотеза об отсутствии различий. Так, если за уровень значимости принято значение р=0,05, то 5 из 100 вычисленных значений р в силу случайности (по теории вероятности) окажется меньше 0,05 (хотя на самом деле верна нулевая гипотеза об отсутствии различий). На практике принято считать, что учет ПМС следует начинать в тех случаях, когда число рассчитываемых значениий более 10).
В STATISTICA для уменьшения влияния множественных сравнений можно установить р на уровне 0,01 или 0,001 вместо 0,05. Считается, что такая поправка в достаточной мере компенсирует множественные парные сравнения, когда таковых избежать не удается:
1. При вторичном анализе данных.
2. При множественных парных сравнениях групп и подгрупп (по демографическим и клиническим характеристикам, исходам, временным точкам и т.д.).
3. При установлении эквивалентности групп в начале нерандомизированного исследования вмешательства.
4. При промежуточном анализе данных, полученных в испытаниях тех или иных вмешательств [7].
Анализ времени жизни в ППО STATISTICAДанные времени жизни имеют две характерные особенности, которые предопределяют специфику их анализа. Прежде всего возможна неполнота данных. Например, в клинических исследовании больные по тем или иным причинам «уходят» из-под наблюдения, часть лабораторных животных может регулярно забиваться для проведения анализов. Реальное же время жизни таких объектов больше длительности наблюдения за ними. Описанный феномен называется цензурированием справа. Наличие цензурированных данных затрудняет оценку эффекта изучаемого воздействия на время жизни, особенно при характеристике отдаленных результатов лечения. Другая особенность данных времени жизни - неадекватность распределения времени жизни статистической модели нормального закона распределения. Конкретный же вид распределения, как правило, неизвестен. Поэтому аппроксимация распределения времени жизни нормальному закону, явная или неявная (при использовании параметрических методов анализа), представляет угрозу для корректности статистических выводов [7,8,9,10].
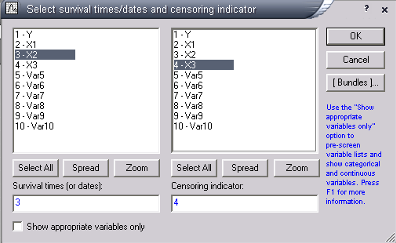
Рис.5—Диалоговое окно в анализе исхода Каплана-Майера.
Как показано на рисунке 5, ППО STATISTICA запрашивает данные о цензурированности (необходим индикатор, указывающий на значение времени (даты) исхода).
Сравнение коэффициентов корреляцииИногда исследователи сталкиваются с проблемой сравнения нескольких коэффициентов корреляции. Так, иногда различия между двумя коэффициентами кажутся очевидными, но при этом не являются статистически значимыми, что в первую очередь может быть обусловлено различием в численности выборок [6].
ППО STATISTICA позволяет автоматически сравнить 2 коэффициента корреляции в Difference test (рис. 6). Достаточными данными являются сами коэффициенты корреляции и численности групп.
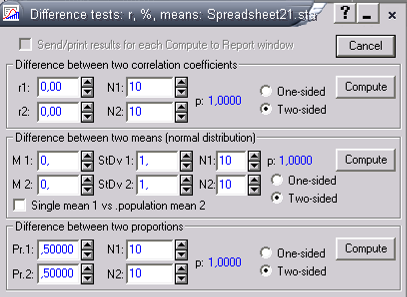
Рис.6—Инструмент «Тест различий» в модуле основной статистики
Практическая часть
В эксперименте была изучена экспрессия CD25 (рецептор к интерлейкину 2) на CD4+ лимфоцитах больных рассеянным склерозом при пролиферативном ответе на МОГ (антиген миелина). Данные получены с помощью проточного цитофлуориметра.
Принята нулевая гипотеза: Процентное содержание пролиферирующих (делящихся) клеток не связано с процентным содержанием CD25-позитивных CD4+ лимфоцитов.
Статистическая обработка данных эксперимента проведена непараметрическими методами в ППО STATISTICA 8.0. В примере приведена вторичная обработка данных с целью показать необходимость последовательного анализа, включая проверку распределения на соответствие закону нормального распределения.
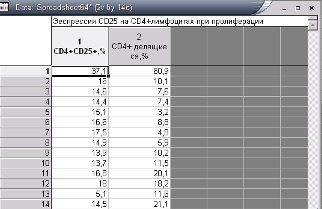
Рис. 7—Анализируемые данные
![]()
Рис. 8—Описательная статистика
Из таблицы, приведенной на рисунке 8, можно сделать предварительные вывод о несоответствии распределения данных з. Гаусса.
В качестве иллюстрации применен параметрический метод анализа связи.


Рис. 9—Коэффициенты корреляции при проведении анализа м.Пирсона и м.Спирмена.
Как показано на рисунке 9, коэффициенты корреляции при проведении анализа м.Пирсона и м.Спирмена не совпадают. По результатам анализа непараметрическим методом корреляции не выявлено, а по м. Пирсона выявлена сильная коррелятивная связь (R=0,83, р<0,05.). Рисунок 9 иллюстрирует распределение данных: одна точка является явно выпадающей.
После исключения выпадающей точки корреляция не выявлена (р>0,05), результат графически представлен на рисунке 11.
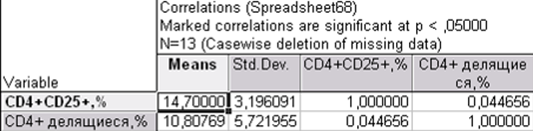

Рис. 11—Коэффициенты корреляции при проведении анализа м.Пирсона и м.Спирмена.
Как при анализе непараметрическим, так и параметрическим методом корреляции выявлено не было.
Таким образом, единственная выпадающая точка при параметрическом анализе данных с распределением, отличным от нормального, дает ложноположительный результат о наличии коррелятивной связи между параметрами.
Как показывает практика, модуль, позволяющий быстро и без дополнительных усилий осуществить проверку типа распределения данных, часто считается избыточным, и к анализу параметрическими методами приступают без доказательств правомочности такого анализа.
Первая попытка обсудить вопросы, связанные со статистической вероятностью, в медицинской литературе была предпринята в 30-х годах XX века. На сегодняшний день в информационной среде, общепонятный и общепринятый язык статистического анализа становится одним из элементов доказательной медицины и биологии.
ППО STATISTICA является мощным инструментом для анализа результатов медико-биологических экспериментов любого уровня сложности, для создания многофакторных моделей и чувствительных тестов оценки эффективности, и только от исследователя зависит качество полученных результатов. Достаточная простота работы в ППО STATISTICA дает возможность самостоятельно анализировать результаты специалистам медико-биологического, а не математического профиля.
Неграмотная работа с данными приводит к грубым систематическим ошибкам, более того, может быть потеряна ценность самих экспериментальных данных при неправильной статистической обработке. Подбор метода остается за исследователем, как и планирование эксперимента с возможностью получения данных от репрезентативных выборок.
Использование ППО STATISTICA сводит к минимуму случайные ошибки в расчётах, дает возможность выбора наиболее адекватного метода анализа и графического представления данных на всех этапах анализа, выявить выпадающие значения. Но ответ на вопрос, подвергать ли дополнительному анализу отдельные выпадающие наблюдения или исключить их, как ошибку измерения, остается за исследователем.
Использование пакетов статистических программ существенно экономит время, позволяя быстро проанализировать большие объемы информации. Последовательные версии ППО STATISTICA (от 6.0 до 8.0) не претерпевают значительных изменений в модулях, необходимых для анализа результатов биологических экспериментов, что также экономит время, так как освоенными методами можно пользоваться в течение многих лет. В то же время, некоторые систематические ошибки анализа могут неоднократно вносить коррективу в результаты экспериментов. Поэтому, использование ППО STATISTICA не исключает необходимость знания исследователем статистических закономерностей.
Статистки основана на сложных математических моделях, и интерпретация результатов должна четко соответствовать закономерностям биологических систем или особенностям клинического использования результатов.
1. Гланц С. Медико-биологическая статистика.—«Практика», —
2. Москва. —1998.—495с.
3. Рокицкий П.Ф. Биологическая статистика. (Изд.' 3-е, испр.) —Минск, — «Вышэйш. школа», —1973. —320 с.
4. Боровиков В.П. Популярное введение в программу STATISTICA. Москва. —2005. —280с.
5. Боровиков В.П. STATISTICA: искусство анализа данных на компьютере – СПб, 2003. – 688с.
6. Куканков Г., Фигурин В. Методы обработки экспериментальных данных. — Минск, —2005. —122с.
7. Реброва О.Ю. Статистический анализ медицинских данных Применение пакета прикладных программ STATISTICA. —М., МедиаСфера, —2002. —312 с.
8. Юнкеров В.И., Григорьев С.Г. Математике-статистическая обработка данных медицинских исследований. —СПб. —ВМсдА, —2002 —266 с.
9. Платонов А.Е. Статистический анализ в медицине и биологии: задачи, терминология, логика, компьютерные методы. — М., —Издательство РАМН, —2000. —52 с.
10. Gore S.M., Jones G., Thompson S.G. The Lancet's statistical review process: areas for improvement by authors. —Lancet. —1992; —№ 340 —Р.100-102.
11. Lang. T. Twenty Statistical Errors Even You Can Find in Biomedical Research Articles. Croatian Medical Journal 2004 —№ 45(4), —Р.361-370