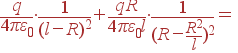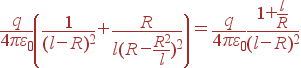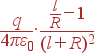Статья: Проводники в электрическом поле. Электростатический метод изображений

М.И. Векслер, Г.Г. Зегря

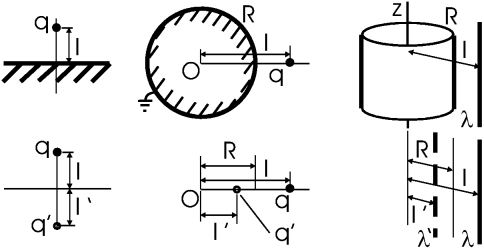
Поле внутри проводника равно нулю, поэтому проводники геометрически ограничивают область, где должны решаться уравнения электростатики. На поверхности проводника φ = const (эквипотенциальность). Это достигается индуцированием зависящей от координаты поверхностной плотности заряда σ. Поле ортогонально к поверхности проводника, но не обязательно однородно. Заряд σ на поверхности связан с полем как σ = ε0E.

Метод изображений состоит в замене системы "заряды + проводящая поверхность" на систему "заряды + изображения". Правила построения изображений обеспечивают эквипотенциальность требуемой поверхности. Для точечного заряда q, расположенного на расстоянии l от плоскости или центра сферы, а также для прямой нити λ, расположенной на расстоянии l от оси цилиндра:

$\left.\right.\hspace{-0.85cm}$ плоскость q → q' = –q, l → l' = l

заземленная сфера q → q' = –qR/l, l → l' = R2/l

цилиндр λ → –λ, l → l' = R2/l

Если сфера не заземлена, то надо еще дополнительно поставить заряд +qR/l в начало координат. Цилиндр и плоскость заземлены по определению (они простираются до бесконечности, где φ = 0).

Основным практическим случаем является проводящая плоскость: например Земля. Он легко обобщается на систему зарядов (нитей, колец и т. д.) - всю ее надо отобразить относительно плоскости.

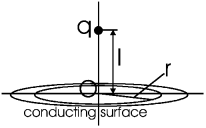
Задача. Точечный заряд q находится на расстоянии l от проводящей плоскости. Найти плотность индуцированного заряда как функцию расстояния r от проекции заряда на плоскость.

Ответ: $\sigma(r) = -\frac{q l}{2\pi(l^2+r^2)^{3/2}}$

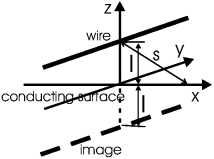
Задача. Бесконечная прямая нить, несущая заряд λ на единицу длины, висит над проводящей плоскостью на расстоянии l от нее. Найти распределение электрического поля и поверхностной плотности индуцированного заряда вблизи плоскости.

Решение: Сначала находим поле одной нити по теореме Гаусса, затем отображаем нить и ищем поле от нити-изображения –λ, далее векторно суммируем эти поля. После этого можно найти σ в любой точке как –ε0· Ewire+image.

Поле одной нити на расстоянии s от нее равно

$E_{wire} = \frac{\lambda}{2\pi\varepsilon_0s}$

и направлено от оси нити или к ней. Поэтому поле одной нити в плоскости на расстоянии x от проекции нити на плоскость будет ( $s = \sqrt{l^2+x^2}$ ):

$E_{wire} = \frac{\lambda}{2\pi\varepsilon_0 \sqrt{l^2+x^2}}$

Такое же по абсолютной величине поле создается нитью-изображением. При векторном суммировании полей двух нитей параллельные плоскости компоненты уничтожаются, а перпендикулярные ей - удваиваются:

$E_{wire+image} = 2\cdot E_{wire, \bot} = 2\cdot E_{wire}\cdot \frac{l}{\sqrt{l^2+x^2}} = \frac{\lambda l} {\pi\varepsilon_0(l^2+x^2)}$

Соответственно, имеем плотность индуцированного заряда:

$\sigma(x) = -\varepsilon_0E_{wire+image} = -\frac{\lambda l}{\pi(l^2+x^2)}$

Проинтегрировав σ(x) по x от –∞ до +∞, можно убедиться, что суммарный индуцированный заряд на единицу длины проекции нити составляет –λ, как и должно быть.

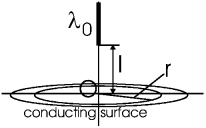
Задача. Очень длинная равномерно заряженная зарядом λ0 нить расположена по оси z и не доходит до проводящей плоскости xy на расстояние l. Найти поле вблизи плоскости xy как функцию расстояния r от начала координат.

Ответ: $\sigma(r) = \frac{\lambda_0}{2\pi\sqrt{l^2+r^2}}$

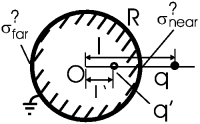
Задача. На расстоянии l от центра заземленной сферы радиуса R<l расположен точечный заряд q. Найти плотность заряда, индуцированного в ближайшей к заряду и в наиболее удаленной от него точках шара.

Решение: По правилам размещения заряда-изображения, помещаем заряд –qR/l в точку на оси "центр сферы - заряд q", удаленную от центра на расстояние R2/l. Тогда расстояние от заряда-изображения до ближайшей к заряду точки сферы будет R–R2/l. В этой точке и поле от истинного заряда, и поле от заряда-изображения направлены к центру сферы, а их сумма по абсолютной величине будет

Enear	=	$\frac{q}{4\pi\varepsilon_0}\cdot\frac{1} {(l-R)^2}+\frac{qR}{4\pi\varepsilon_0l}\cdot\frac{1}{(R-\frac{R^2}{l})^2} =$
	=	$\frac{q}{4\pi\varepsilon_0}\left(\frac{1}{(l-R)^2} + \frac{R}{l(R-\frac{R^2}{l})^2}\right) = \frac{q}{4\pi\varepsilon_0} \frac{1+\frac{l}{R}}{(l-R)^2}$

Сразу же находится σ:

$\sigma_{near} = -\varepsilon_0 E_{near} = -\frac{q}{4\pi(l-R)^2}\cdot\left(1+\frac{l}{R}\right)$

Аналогично находим плотность индуцированного заряда в удаленной точке, только там поле от заряда q направлено от центра, а от изображения - на центр. Сумма этих полей оказывается направленной к центру и по модулю равной:

Efar

$\frac{q}{4\pi\varepsilon_0}\cdot \frac{\frac{l}{R}-1}{(l+R)^2}$

так что

$\sigma_{far} = -\varepsilon_0 E_{far} = -\frac{q}{4\pi(l+R)^2}\cdot\left(\frac{l}{R}-1\right)$

Список литературы

1. И.Е. Иродов, Задачи по общей физике, 3-е изд., М.: Издательство БИНОМ, 1998. - 448 с.; или 2-е изд., М.: Наука, 1988. - 416 с.

2. В.В. Батыгин, И.Н. Топтыгин, Сборник задач по электродинамике (под ред. М.М. Бредова), 2-е изд., М.: Наука, 1970. - 503 с.

3. Л.Д. Ландау, Е.М. Лифшиц, Теоретическая физика. т.8 Электродинамика сплошных сред, 2-е изд., М.: Наука, 1992. - 661 с.

Для подготовки данной работы были использованы материалы с сайта http://edu.ioffe.ru/r