
Рефераты по международному публичному праву
Рефераты по международному частному праву
Рефераты по международным отношениям
Рефераты по культуре и искусству
Рефераты по менеджменту
Рефераты по металлургии
Рефераты по муниципальному праву
Рефераты по налогообложению
Рефераты по оккультизму и уфологии
Рефераты по педагогике
Рефераты по политологии
Рефераты по праву
Биографии
Рефераты по предпринимательству
Рефераты по психологии
Рефераты по радиоэлектронике
Рефераты по риторике
Рефераты по социологии
Рефераты по статистике
Рефераты по страхованию
Рефераты по строительству
Рефераты по таможенной системе
Сочинения по литературе и русскому языку
Рефераты по теории государства и права
Рефераты по теории организации
Рефераты по теплотехнике
Рефераты по технологии
Рефераты по товароведению
Рефераты по транспорту
Рефераты по трудовому праву
Рефераты по туризму
Рефераты по уголовному праву и процессу
Рефераты по управлению
Курсовая работа: Уравнивание геодезических сетей сгущения упрощенным способом
Курсовая работа: Уравнивание геодезических сетей сгущения упрощенным способом
Курсовая работа
УРАВНИВАНИЕ ГЕОДЕЗИЧЕСКИХ СЕТЕЙ СГУЩЕНИЯ УПРОЩЕННЫМИ СПОСОБАМИ
Введение
1. Вычисление координат дополнительного пункта, определяемого прямой многократной засечкой
1.1 Исходные данные
1.2 Составление схемы расположения определяемого и исходных пунктов
1.3 Выбор наилучших вариантов засечки
1.4 Решение наилучших вариантов засечки
1.5 Оценка ожидаемой точности полученных результатов
2. Вычисление координат дополнительного пункта, определенного обратной многократной засечкой
2.1 Общие указания и исходные данные
2.2 Составление схемы расположения определяемого и исходного пунктов
2.3 Выбор наилучших вариантов засечки
2.4 Решение наилучших вариантов засечки
2.5 Оценка ожидаемой точности результатов
3 Уравнивание ходов полигонометрии второго разряда, образующих одну узловую точку
3.1 Общие указания и исходные данные
3.2 Вычисление координат исходных пунктов и дирекционных углов исходных направлений
3.3 Вычисление и уравнивание дирекционного угла узловой стороны
3.4 Вычисление и уравнивание координат узловой точки
3.5 Уравнивание приращений координат и вычисление координат всех точек
4. Уравнивание ходов технического нивелирования способом полигонов профессора В.В. Попова
4.1 Общие указания и исходные данные
4.2 Уравнивание превышений по способу полигонов профессора В.В.Попова
4.3 Вычисление высот точек по ходам, по уравненным превышениям
4.4 Оценка точности полученных результатов
Заключение
Список используемой литературы
Перечень сокращений
Мм - миллиметры
М – метры
Км – километры
Табл. – таблица
Прил. - приложение
Т.е. – то есть
Т.о. – таким образом
Целью курсовой работы является освоение методики математической обработки результатов геодезических измерений в сетях сгущения при выполнении следующих заданий:
1. вычисление координат дополнительных пунктов, определённых прямой и обратной многократными угловыми засечками;
2. раздельного уравнивания системы ходов полигонометрии второго разряда с одной узловой точкой;
3. уравнивания превышений технического нивелирования по способу полигонов профессора В.В.Попова.
Для проведения работы, связанной с использованием земли требуется изучение форм, рельефа, расположения объектов и производство специальных измерений, вычислительная обработка и составление карт, планов и профилей, которые служат основной продукцией геодезических работ и дают представление о форме и размерах поверхностей всей земли или отдельных ее частей.
Материалом для выполнения заданий служат результаты полевых измерений углов и превышений, которые приводятся как исходные данные.
В наше время, когда земля приобретает все большую ценность, стали очень актуальны геодезические измерения и вычисления. Без базовых знаний, которые я освоила в результате выполнения курсовой работы, невозможно решение многих геодезических задач, что мне придется решать в моей будущей профессии. На данный момент актуальность этой курсовой работы состоит в том, что я ознакомилась с теми видами работ, которые предстоит выполнять на летней практике.
С внедрением в геодезическую науку более точных электронных приборов ошибки измерений могут значительно уменьшиться.
1. Вычисление координат дополнительного пункта, определяемого прямой многократной засечкой
Прямая засечка - это задача по определению третьего пункта по двум данным пунктам и двум измеренным при этих пунктах углам. Для контроля правильности вычисления координат засечку делают многократной.
Я нашла индивидуальные поправки:
∆β’ = 3*N = 3*4 = 12’
∆x = ∆y = 25,50*N = 25,50*4 = 102м
Таблица 1 – Исходные данные для решения прямой засечки.
| обозначения | измеренные направления |
исправленные направления с учётом № |
координаты | ||||||
| градусы | минуты | секунды | градусы | минуты | секунды | X | Y | ||
| A | P | 0 | 0 | 0 | 0 | 0 | 0 | 5552,55 | 2402,09 |
| B | 88 | 44 | 20 | 88 | 56 | 20 | |||
| B | A | 0 | 0 | 0 | 0 | 0 | 0 | 4853,04 | 2151,60 |
| P | 43 | 16 | 20 | 43 | 04 | 20 | |||
| C | 72 | 57 | 28 | 72 | 57 | 28 | |||
| C | B | 0 | 0 | 0 | 0 | 0 | 0 | 4813,24 | 3008,33 |
| P | 91 | 15 | 39 | 91 | 03 | 39 | |||
Порядок решения задачи:
1. составление схемы расположения определяемого и исходных пунктов
2. выбор наилучших вариантов засечки
3. решение наилучших вариантов засечки
4. оценка ожидаемой точности полученных результатов.
1.2 Составление схемы расположения определяемого и исходных пунктов
Составление схемы я произвела на листе миллиметровой бумаги формата А4. При этом оцифровала в масштабе 1:10000. По координатам из таблицы 1 нанесла исходные пункты А, В, С. Искомый пункт Р нанесла по углам с помощью геодезического транспортира. Схема представлена в приложении А.
1.3 Выбор наилучших вариантов засечки
Для определения наилучших вариантов засечки произвела построение инверсионных треугольников. Для этого на схеме из приложения А сделала следующие построения:
- от пункта Р по направлениям РА, РВ, РС отложила отрезки r, длину которых вычислила по формуле:
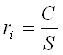 , (1) где
, (1) где
С – произвольно выбранное число
S – расстояние от определяемого пункта до исходного, измеренное по схеме в сантиметрах.
Для моего варианта:
С=10 , S1=6,8 см, S2=10,1 см, S3=5,1 см
r1=1,47 см, r2=0,99 см, r3=1,96 см
Вершинами инверсионных треугольников являются пункт Р и конечные точки соответствующих отрезков ri . Лучшие варианты засечки – те, у которых самые большие площади инверсионных треугольников (определяем визуально). На моей схеме это треугольники r1r3P и r2r3P, следовательно, для решения нужно использовать засечки РАС и ВРС, но засечка РАС не может быть использована из-за того, что неизвестен угол РАС. Поэтому для нахождения координат точки Р я использовала засечки АВР и СВР (обозначения согласно прил. 1).
1.4 Решение наилучших вариантов засечки
Для решения вариантов засечки будем использовать формулы Юнга:
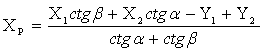
![]() (2)
(2)
где X1, X2, Y1, Y2 – координаты исходных пунктов
α, β – горизонтальные углы, измеренные на исходных пунктах.
В формулах (2) обозначения соответствуют схеме, изображенной на рисунке 1.
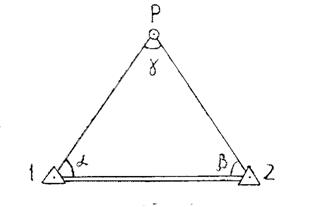
Рисунок 1 – Схема к вычислениям прямой засечки.
Используя формулы (2) вычислила координаты определяемого пункта Р, результаты вычислений приведены в таблице 2.
Таблица 2 – Вычисление вариантов прямой засечки.
| обозначения | углы | X | ctg α, ctg β | Y | |||
| пунктов | углов | градусы | минуты | секунды | ctg α + ctg β | ||
| 1(A) | α | 88 | 56 | 20 | 5552,55 | 0,018522 | 2402,09 |
| 2(B) | β | 43 | 04 | 20 | 4853,04 | 1,069662 | 2151,60 |
| P | 5310,45 | 1,088184 | 3040,65 | ||||
| 1(B) | α | 29 | 53 | 08 | 4853,04 | 1,740068 | 2151,60 |
| 2(C) | β | 91 | 03 | 39 | 4813,,24 | -0,018517 | 3008,33 |
| P | 5310,46 | 1,721551 | 3040,66 | ||||
Расхождение координат, полученных при решении двух вариантов засечки, с учетом точности измерений допускается до 0,2 м.
В моём случае расхождение по Х составило 0,1 м, и по Y - 0,1 м. расхождения находятся в допуске, следовательно, за окончательные значения координат принимаем средние значения двух вариантов.
Среднее Х=5310,455
Среднее Y=3040,655
1.5 Оценка ожидаемой точности полученных результатов
Я определила среднюю квадратическую ошибку положения точки для каждого варианта засечки по формуле:
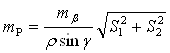 (3)
(3)
где mβ – средняя квадратическая ошибка измерения углов (в задании принимаем mβ=10''),
![]() - угол в треугольнике при точке Р,
- угол в треугольнике при точке Р,
S1, S2 – стороны засечки, м (определены по схеме),
![]() =206265''.
=206265''.
Среднюю квадратическую ошибку координат, полученных из двух вариантов засечки, нашла из формулы:
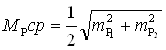 (4).
(4).
углы γ нашла по определению, что сумма углов треугольника равна 180°: для АВР γ=180°-(88°56'20''+43°04'20'')=47°59'20''
для СВР γ=180°-(29°53'08''+91°03'39'')=59°03'13''
![]()
![]()
Из формулы (4) нащла среднюю квадратическую ошибку координат, полученных из двух вариантов засечки:
![]() м
м
Итак, в этой задаче я решила два варианта прямой многократной засечки и вычислила координаты дополнительного пункта. Расхождения координат, полученных в первом и втором вариантах засечки оказались в допуске, поэтому за окончательное значение координат исходного пункта Р я приняла Х=5310,455 и Y=3040,655. При оценке точности полученных результатов получила следующие ошибки:
- среднюю квадратическую ошибку положения торчки Р для каждого варианта засечки: mp1=0,079 м, mp2=0,064 м
- среднюю квадратическую ошибку координат, полученных из двух вариантов засечки: Mp Cp=0,051 м
2. Вычисление координат дополнительного пункта, определенного обратной многократной засечкой
2.1 Общие указания и исходные данные
Обратная засечка – это задача по определению четвертого пункта по трем данным пунктам и двум измеренным при определяемом пункте углам.
Для контроля правильности решения задачи при определяемой точке измеряют третий угол между направлениями на один из первых трех пунктов и на четвертый данный пункт.
Таким образом, для решения задачи с контролем необходимо видеть из определяемой точки четыре пункта исходной сети и измерить при определяемой точке три угла.
При решении задачи я воспользовалась исходными данными, исправленными с учетом порядкового номера, которые приведены в таблице 3.
Таблица 3 – Исходные данные для решения обратной засечки.
| название пункта | координаты |
измеренные на пункте Р направления |
|
| X | Y | ||
| 1 | 7105,31 | 3851,55 |
0 |
| 2 | 6613,86 | 3816,43 |
59 |
| 3 | 6653,66 | 2959,70 |
177 |
| 4 | 7353,17 | 3210,20 |
273 |
Порядок решения задачи:
1. составление схемы расположения определяемого и исходных пунктов
2. выбор наилучших вариантов засечки
3. решение наилучших вариантов засечки
4. оценка ожидаемой точности полученных результатов.
2.2 Составление схемы расположения определяемого и исходного пунктов
Составление схемы я произвела на листе миллиметровой бумаги формата А4. При этом оцифровала её в масштабе 1:10000. По координатам из таблицы 3 нанесла исходные пункты А, В, C, D (приложение Б). Искомый пункт Р нанесла по направлениям (по способу Болотова) на листе кальки формата А4 (приложение В).
2.3 Выбор наилучших вариантов засечки
Для выбора лучших вариантов засечки производятся те же действия, что и при прямой засечке:
- строятся инверсионные треугольники (вершинами этих треугольников будут только конечные точки отрезков ri)
- визуально определяются треугольники с большими площадями, и именно они выбираются для решения обратной засечки.
В моем варианте были выбраны треугольники 3-4-1 и 3-4-2 для решения.
2.4 Решение наилучших вариантов засечки
Вычисление координат дополнительного пункта, определенного обратной многократной засечкой, приведены в табл. 4.
Таблица 4 - Схема для вычислений обратной угловой засечки.
| обозначение пунктов | координаты | - | ∆XBC | - | ΔYBC | |
| A | XA | YA | αAP | - | tg αAP | - |
| β2 | ∆XBC | ctg β2 | ΔYBC | |||
| B | XB | YB | αBP | - | tg αBP | - |
| β3 | ∆XCA | ctg β3 | ΔYCA | |||
| C | XC | YC | - | ∑ | - | ∑ |
| P | XP | YP | YP’ | ∆X0 |
tg αAP - tg αBP |
ΔY0 |
Для решения задачи сначала я определила дирекционный угол направления АР, принятого в качестве главного, по формуле Деламбра:
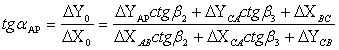 (5),
(5),
далее определяем дирекционный угол следующего направления:
![]() (6).
(6).
После того, как определила дирекционные углы направлений АР и ВР, вычислила координаты точки Р по формулам Гаусса:
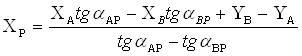 (7)
(7)
![]() (8)
(8)
Для контроля вычислений применила формулу:
![]() (9).
(9).
В формулах (5-9) обозначения соответствуют схеме, представленной на рисунке 2.
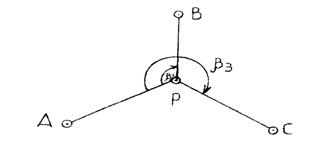
Рисунок 2 – Схема обозначений к вычислениям.
Решение задачи представлено в таблицах 5 и 6.
Таблица 5 – Решение обратной угловой засечки.
| Обозначение пунктов | координаты | - | -247,86 | - | 641,35 | |
| 3 (A) | 6653,66 | 2959,70 |
241 |
- | 1,865475 | - |
|
95 |
699,51 | -0,102443 | 250,50 | |||
| 4 (B) | 7353,17 | 3210,20 |
337 |
- | -0,411042 | - |
|
182 |
-451,65 | 21,427930 | -891,85 | |||
| 1 (С) | 7150,31 | 3851,55 | - | 0 | - | 0 |
| P | 6890,00 | 3400,58 | 3400,58 | -10390,93 | 2,276517 | -19384,02 |
Таблица 6 – Решение обратной угловой засечки.
| Обозначение пунктов | координаты | - | -739,31 | - | 606,23 | |
| 3 (A) | 6653,66 | 2959,70 |
241 |
- | 1,865398 | - |
|
95 |
699,51 | -0,102443 | 250,50 | |||
| 4 (B) | 7353,17 | 3210,20 |
337 |
- | -0,411065 | - |
|
241 |
39,8 | 0,536601 | -856,73 | |||
| 2 (C) | 6613,86 | 3816,43 | - | 0 | - | 0 |
| P | 6890,01 | 3400,59 | 3400,59 | -656,53 | 2,276463 | -1224,69 |
Координаты в двух вариантах различны, но расхождения не превышают 0,2 м, за окончательные значения координат принимаем их средние значения:
Среднее Х=6890,005
Среднее Y=3400,585.
2.5 Оценка ожидаемой точности результатов
Далее я вычислила среднюю квадратическую ошибку положения определяемого пункта:
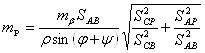 (10),
(10),
где ![]() -
средняя квадратическая ошибка измерения углов (10''),
-
средняя квадратическая ошибка измерения углов (10''),
S – расстояния, измеренные по схеме, м,
![]() =
=![]() ,
,
![]() - углы, измеряемые
транспортиром по схеме.
- углы, измеряемые
транспортиром по схеме.
Среднюю квадратическую ошибку координат, полученных как средние значения из двух вариантов, вычислила по формуле:
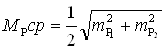 (11).
(11).
Из формулы (10) средняя квадратическая ошибка положения определяемого пункта:
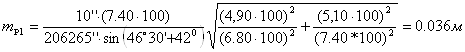
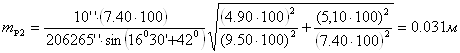
Из формулы (11) нашла среднюю квадратическую ошибку координат, полученных как средние значения из двух вариантов:
![]()
Итак, в этой задаче было решено два наилучших варианта засечки. Для решения задачи была построена схема расположения определяемого и исходных пунктов, выбраны наилучшие варианты засечки с помощью инверсионных треугольников, решены эти варианты засечки. Координаты пункта Р, полученные в двух вариантах, оказались в допуске и за окончательные значения координат были приняты их средние значения: среднее Х=6890,005 м, среднее Y=3400,585 м.
Вычисления были выполнены со следующими ошибками:
- средняя квадратическая ошибка положения определяемого пункта: mp1=0,036 м и mp2=0,031 м
- средняя квадратическая ошибка координат, полученных как средние значения из двух вариантов: МpСр=0,02 м
уравнивание геодезическая сеть сгущение засечка
3. Уравнивание ходов полигонометрии второго разряда, образующих одну узловую точку
3.1 Общие указания и исходные данные
ПОЛИГОНОМЕТРИЯ (от греч. polygonos - многоугольный и ...метрия), метод определения взаимного положения точек земной поверхности для построения опорной геодезической сети путем измерения длин прямых линий, связывающих эти точки, и горизонтальных углов между ними. Применяется в залесенной и застроенной местности вместо триангуляции.
Наилучший результат получается при совместном уравнивании всех измеренных величин. Число измерений в полигонометрической сети велико, измеренные величины разнородны (углы и расстояния), сеть имеет сложную форму. Строгое уравнивание на практике выполняется чрезвычайно редко, так как представляет собой сложную и трудоёмкую задачу.
Задача уравнивания значительно облегчается при последовательном несовместном уравнивании. При этом сначала уравнивают углы, а затем приращения координат (абсцисс и ординат). Полученные таким образом результаты будут отличаться от результатов строгого уравнивания полигонометрической сети.
Заданием предусмотрено выполнить уравнивание системы ходов раздельным способом.
3.2 Вычисление координат исходных пунктов и дирекционных углов исходных направлений
По данным, изменённым в соответствии с порядковым номером, я вычислила координаты исходных пунктов и дирекционные углы исходных направлений. Вычисление произвела в таблице 7.
Таблица 7 – Данные по исходным пунктам.
пункт |
углы | дирекционные углы | Сторона, м | Координаты, м | |||||
| град. | мин. | сек. | град. | мин. | сек. | X | Y | ||
| A | 43 | 54 | 55 | 2349486,73 | 9475377,12 | ||||
| 144 | 17 | 33 | 3301,47 | ||||||
| B | 103 | 52 | 34 | 2346805,92 | 9477304,01 | ||||
| 220 | 24 | 59 | 4296,16 | ||||||
| C | 32 | 12 | 31 | 2343535,03 | 9474518,65 | ||||
| 8 | 12 | 28 | 6013,30 | ||||||
| A | 43 | 54 | 55 | 2349486,73 | 9475377,12 | ||||
| 144 | 17 | 33 | |||||||
Дирекционные углы направлений ВС, СА были вычислены по формуле:
![]() (12),
(12),
приращения координат:
![]() и
и ![]() (13),
(13),
координаты исходных пунктов:
![]() и
и ![]() (14).
(14).
3.3 Вычисление и уравнивание дирекционного угла узловой стороны
За узловую я приняла сторону 6-7.
Вычисления при уравнивании дирекционного угла узловой стороны занесла в таблицу 8.
Таблица 8 – Схема к вычислениям при уравнивании дирекционного угла стороны 6-7.
|
№ хода |
кол-во углов | вес хода P=c/n | Сумма измерен.углов ∑β | Исходный дирекционный угол αисх | Дирекционный угол узловой стороны αi |
|
|
|
| 1 | 7 | 1,429 |
1385 |
324 |
199 |
33” | 3” |
|
| 2 | 6 | 1,667 |
1025 |
144 |
199 |
42” | 5” |
|
| 3 | 7 | 1,429 |
1101 |
220 |
199 |
17” | -8” |
|
Дирекционный угол стороны 6-7 вычислен по формуле:
![]() (15).
(15).
![]() 1= 324
1= 324![]() 17’33” +
180
17’33” +
180![]() * 7 - 1385
* 7 - 1385![]() 12’10” = 199
12’10” = 199![]() 05’23”
05’23”
![]() 2= 144
2= 144![]() 17’33” +
180
17’33” +
180![]() * 6 - 1025
* 6 - 1025![]() 12’08” = 199
12’08” = 199![]() 05’25”
05’25”
![]() 3= 220
3= 220![]() 24’59” +
180
24’59” +
180![]() * 7 - 1101
* 7 - 1101![]() 19’47” = 199
19’47” = 199![]() 05’12”
05’12”
Наивероятнейшее значение дирекционного угла узловой линии по данным всех ходов найдено по формуле:
![]() (16),
(16),
где ![]() ,
,
![]() - приближенное значение
- приближенное значение ![]() .
.
![]()
Угловые невязки вычислены по формуле:
![]() (17).
(17).
Допустимые значения невязок:
![]() (18).
(18).
Все значения невязок оказались в допуске, значит можно ввести поправки во все измеренные углы.
3.4 Вычисление и уравнивание координат узловой точки
По уравненным углам я вычислила дирекционные и углы и приращения координат для всех ходов.
По данным каждого хода вычислила координаты узловой точки по формулам:
![]() и
и ![]() (19).
(19).
![]() 1 = 2349486,73 + (-2967) = 2346519,73 м
1 = 2349486,73 + (-2967) = 2346519,73 м
![]() 1 = 9475377,12 + (-456,22) = 9474920,90
м
1 = 9475377,12 + (-456,22) = 9474920,90
м
![]() 2 = 2346805,92 + (-286,16) =2346519,76 м
2 = 2346805,92 + (-286,16) =2346519,76 м
![]() 2 = 9477304,01 + (-2383,07) =9474920,94
м
2 = 9477304,01 + (-2383,07) =9474920,94
м
![]() 3 = 2343535,03 + 2984,74 = 2346519,77 м
3 = 2343535,03 + 2984,74 = 2346519,77 м
![]() 3 = 9474518,65 + 402,19 = 9474920,84 м
3 = 9474518,65 + 402,19 = 9474920,84 м
Приведены расчеты для первого хода.
По формулам:
![]() и
и ![]() (20)
(20)
я нашла вероятнейшие значения координат по данным всех ходов.
![]()
![]()
3.5 Уравнивание приращений координат и вычисление координат всех точек
Вычисления при уравнивании координат узловой точки приведены в таблице 9.
Таблица 9 – Схема к вычислениям при уравнивании координат узловой точки.
| периметр хода | вес хода | сумма приращений | координаты узловой точки | невязки по ходам | |||||
| ∆X | ∆Y | X | Y | δX | δY | δXY | δXY/S | ||
| 3001,938 | 0,0033 | -2967 | -456,22 | 2349486,73 | 9475377,12 | -0,02 | 0 | 0,02 | 1/150100 |
| 2451,275 | 0,0041 | -286,16 | -2383,07 | 2346805,92 | 9477304,01 | +0,01 | +0,04 | 0,04 | 1/59452 |
| 3068,592 | 0,0033 | 2984,74 | 402,19 | 2343535,03 | 9474518,65 | +0,02 | -0,06 | 0,06 | 1/48519 |
![]()
Для вычисления относительных невязок необходимо было произвести предварительные вычисления:
![]()
![]()
![]() (21).
(21).
Относительную невязку вычислила по формуле:
![]()
![]() (22)
(22)
и сравнила с величиной 1/5000, невязка меньше этой величины, следовательно, она допустима.
Ввела поправки в приращения координат пропорционально длинам сторон.
После уравнивания приращений координат вычислила координаты всех точек ходов.
Вычисления задания представлены в таблице 10.
Таблица 10 – Вычисления при уравнивании ходов полигонометрии второго разряда
| № | углы | дирекционные углы | стороны | приращения координат | координаты | ||||||||
| град. | мин. | сек. | град. | мин. | сек. | ∆Х | ∆Y | X | Y | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| первый ход | |||||||||||||
| В | |||||||||||||
| 324 | 17 | 33 | |||||||||||
| А | 315 | 7 | 35 | +0,01 | 2349486,73 | 9475377,1 | |||||||
| 189 | 09 | 58 | 497,140 | -490,79 | -79,19 | ||||||||
| 1 | 180 | 56 | 36 | 2348995,95 | 9475297,9 | ||||||||
| 188 | 13 | 22 | 502,751 | -497,58 | -71,90 | ||||||||
| 2 | 179 | 4 | 17 | 2348498,37 | 9475226,0 | ||||||||
| 189 | 09 | 04 | 500,857 | -494,48 | -79,65 | ||||||||
| 3 | 180 | 13 | 32 | 2348003,89 | 9475146,3 | ||||||||
| 188 | 55 | 33 | 511,387 | -505,19 | -79,34 | ||||||||
| 4 | 180 | 25 | 45 | +0,01 | 2347498,70 | 9475067,0 | |||||||
| 188 | 29 | 48 | 478,306 | -473,06 | -70,67 | ||||||||
| 5 | 180 | 0 | 44 | 2347025,65 | 9474996,3 | ||||||||
| 188 | 29 | 04 | 511,497 | -505,90 | -75,47 | ||||||||
| 6 | 169 | 23 | 44 | 2346519,75 | 9474920,9 | ||||||||
| 199 | 05 | 20 | |||||||||||
| 7 | |||||||||||||
| ∑ | 1385 | 12 | 10 | 3001,938 | -2967 | -456,22 | |||||||
| второй ход |
|
||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|
|||||
| 144 | 17 | 33 |
|
||||||||||||||
| В | 66 | 49 | 31 | -0,01 | 2346805,92 | 9477304,01 |
|
||||||||||
| 257 | 28 | 01 | 512,727 | -111,26 | -500,51 |
|
|||||||||||
| 13 | 180 | 0 | 18 | -0,01 | 2346694,66 | 9476803,49 |
|
||||||||||
| 257 | 27 | 43 | 508,706 | -110,43 | -496,57 |
|
|||||||||||
| 14 | 179 | 59 | 42 | -0,01 | -0,01 | 2346584,23 | 9476306,91 |
|
|||||||||
| 257 | 28 | 01 | 521,445 | -113,15 | -509,02 |
|
|||||||||||
| 15 | 180 | 0 | 3 | 2346471,07 | 9475798,88 |
|
|||||||||||
| 257 | 27 | 58 | 427,178 | -92,70 | -416,99 |
|
|||||||||||
| 16 | 150 | 22 | 50 | -0,01 | 2343378,37 | 9475380,89 |
|
||||||||||
| 287 | 05 | 07 | 481,219 | 141,38 | -459,98 |
|
|||||||||||
| 6 | 267 | 59 | 46 | 2346519,75 | 9474920,90 |
|
|||||||||||
| 199 | 05 | 20 |
|
||||||||||||||
| 7 |
|
||||||||||||||||
|
|||||||||||||||||
| ∑ | 1025 | 12 | 08 | 2451,275 | -286,16 | -2383,07 |
|
||||||||||
|
|||||||||||||||||
| третий ход |
|
||||||||||||||||
| В | |||||||||||||||||
| 220 | 24 | 59 | |||||||||||||||
| С | 27 | 23 | 1 | -0,01 | +0,01 | 2343535,03 | 9474518,65 | ||||||||||
| 13 | 01 | 58 | 504,716 | 491,72 | 113,82 | ||||||||||||
| 12 | 180 | 7 | 35 | -0,01 | 2344026,74 | 9474632,48 | |||||||||||
| 12 | 54 | 24 | 506,8 | 494,00 | 113,20 | ||||||||||||
| 11 | 179 | 55 | 47 | +0,01 | 2344520,73 | 9474745,68 | |||||||||||
| 12 | 58 | 37 | 497,121 | 484,42 | 111,63 | ||||||||||||
| 10 | 180 | 1 | 19 | +0,01 | 2345005,15 | 9474857,32 | |||||||||||
| 12 | 57 | 18 | 454,503 | 442,93 | 101,89 | ||||||||||||
| 9 | 202 | 28 | 30 | +0,01 | 2345448,08 | 9474959,22 | |||||||||||
| 350 | 28 | 48 | 411,747 | 406,08 | -68,09 | ||||||||||||
| 8 | 183 | 44 | 41 | +0,01 | 2345854,16 | 9474891,14 | |||||||||||
| 346 | 44 | 07 | 354,236 | 344,79 | -81,28 | ||||||||||||
| 7 | 147 | 38 | 46 | +0,01 | 2346198,95 | 9474809,87 | |||||||||||
| 379 | 05 | 20 | 339,469 | 320,80 | 111,02 | ||||||||||||
| 6 | 2346519,75 | 9474920,90 | |||||||||||||||
| ∑ | 1101 | 19 | 47 | 3068,592 | 2984,74 | 402,19 | |||||||||||
При решении этой задачи я научилась уравнивать ходы полигонометрии второго разряда раздельным способом. Усвоила, что при этом способе необходимо сначала уравнять углы, затем уравнивать приращения координат и уже по уравненным приращениям вычислять координаты.
4. Уравнивание ходов технического нивелирования способом полигонов профессора В.В. Попова
4.1 Общие указания и исходные данные
Простой и в то же время строгий способ уравнивания ходов технического нивелирования способом полигонов предложил профессор В.В.Попов. Этот способ сводится к последовательному распределению невязок в каждом полигоне пропорционально длинам ходов. При этом если в соседнем полигоне уже было произведено распределение невязок, то на величину поправки, пришедшейся на общий обоим полигонам ход, нужно предварительно исправить с учётом её знака невязку этого подлежащего увязанию полигона. Таким образом, дело сводится к методу последовательных приближений. Применение способа Попова требует расположения вычислений в определенной схеме. Удобно эти вычисления производить на схеме расположения ходов, как это рекомендует сам автор.
Перед уравниваем я вычертила схему нивелирной сети (приложение Г), на которую выписала по ходам и полигонам периметры, измеренные превышения, фактические и допустимые невязки в сумме превышений по полигонам. Для установления знака невязки направление обхода в каждом полигоне выбрала по ходу часовой стрелки. Контролем правильности вычисления невязок является условие [fh]=0. вычислила допустимые невязки по формуле:
fh доп= ±20√L (23),
где L – периметр полигона, км.
Предварительно исправила
исходные данные, учитывая свой порядковый номер. Эти вычисления производятся в
таблице 11. Длину ходов вычислила по формуле: ![]() ,
(24),
,
(24),
∆l = +0.2км * №=0,16 км. Высота исходных реперов HRp1=106.985 –
3мм * №=106,973 м, H Rp2=100.132 м.
4.2 Уравнивание превышений по способу полигонов профессора В.В.Попова
Далее вычертила схему независимых нивелирных полигонов, на которую выписала невязки полигонов (приложение Д). Невязки в превышениях выписаны внутри соответствующих полигонов в прямоугольных рамках. Полигоны пронумерованы.
Рядом с ходами, идущими по периметру полигонов, подготовила таблички для записи значений поправок. Поправки по каждому ходу выбрасывались за полигон, таким образом для внутренних ходов – по две таблички и по одной с каждой внешней стороны.
Для каждого хода вычислила коэффициент пропорциональности или «красные числа» по формуле:
ri=![]() (25),
(25),
где Li – длина хода, [L] – периметр хода. Найденные
отношения выписала на схему над табличками поправок для каждого хода красным
цветом. Контролем правильности вычисления этих чисел является равенство ![]() =
=![]() по каждому полигону
(например, для полигона I
«красные числа» получились 0.22, 0.25, 0.28, 0.25, в сумме они действительно
дают единицу).
по каждому полигону
(например, для полигона I
«красные числа» получились 0.22, 0.25, 0.28, 0.25, в сумме они действительно
дают единицу).
Начала распределение невязок с полигона, имеющего наибольшую по абсолютной величине невязку. В моем варианте этим полигоном является полигон II с невязкой -14. Невязки в полигонах распределяют пропорционально «красным числам». Итак, умножала невязку полигона на соответствующие этому полигону «красные числа», округляя до целых, и записывала в таблички, лежащие вне полигона, причем со знаком, одинаковым знаку невязки. Контролем является: сумма поправок должна дать величину невязки.
Перешла к следующему полигону (III). В нем ход 12-13 уже получил поправку, поэтому невязку этого полигона следовало изменить на величину поправки хода 12-13. Полученная остаточная невязка вписывается в рамку под числом исходной невязки полигона III. Далее эту остаточную невязку умножала на соответствующие этому полигону «красные числа». Полученные поправки выписываем в рамки, находящиеся вне этого полигона. Каждый раз производила контроль вычислений!
И так далее, переходила к следующему полигону по часовой стрелке и выполняем те же операции (исправляла исходную невязку полигона с учетом поправок, пришедших из других полигонов, и распределяла поправки пропорционально «красным числам», выполняя контроль). Так, когда вернулась к полигону II, значит завершила первый круг распределения невязок. Перешла ко второму кругу, повторяя все в том же порядке.
В полигоне II невязку я уже распределила, но в этом полигоне имеются поправки, пришедшие из других полигонов. Сложив их, получила новую невязку этого полигона, которую должна распределить вышеописанным порядком, вписывая вторичные поправки по ходам в соответствующие рамки.
Таким же путем прошла по всем другим полигонам во втором круге. После перешла к третьему, четвертому и так далее. В моем случае, потребовалось пройти 5 кругов.
Теперь необходимо в каждой рамке подсчитать алгебраическую сумму поправок. Для внешних ходов нужно у найденных результатов сложения по каждому ходу изменить знак на обратный и перенести внутрь полигона. Так, например, у хода 2-12 поправка равна -19, перенеся ее внутрь II-ого полигона, получим поправку для хода 2-12, равную 19. Для общих ходов каждой пары смежных полигонов имеются по две рамки, расположенные по разные стороны хода. Вычислила поправки по каждому ходу как разность между суммами поправок по внутренней и внешней табличкам. Эти величины вписала при данном ходе, каждую внутри соответствующего полигона.
Контролем служит то, что сумма поправок по всем ходам полигона должна дать взятую с обратным знаком величину первоначальной невязки, приходящуюся на данный ход (в моем случае по каждому полигону получилось, что сумма поправок по всем ходам совпала с первоначальной невязкой, взятой с противоположным знаком:
по I полигону – 12 мм, по II – 14 мм , по III - 8 мм, по IV - 14 мм, по V – 12мм).
4.3 Вычисление высот точек по ходам, по уравненным превышениям
Далее, т.к. контроль выполнился, вычислила уравненные превышения между точками нивелирования и высоты точек по каждому ходу. Поправки в измеренные превышения нашла, распределяя поправку на ход пропорционально числу станций между точками нивелирования.
Таблица 11 - Измеренные величины и результаты уравнивания
| № хода | № точки | длина хода, Li, км | число станций |
Превы шения, м |
Поправки, мм | уравненные | |
| Превышения, м | Высоты, м | ||||||
| 1 | 2 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | Rp1 | 106,973 | |||||
| 1 | 4,8 | 29 | -3,979 | +5 | -3,974 | 102,999 | |
| 2 | 7,1 | 35 | -1,251 | +6 | -1,245 | 101,754 | |
| ∑ | 11,9 | 64 | -5,23 | +11 | -5,219 | ||
| 2 | 2 | 101,754 | |||||
| 3 | 6,3 | 36 | -1,098 | +2 | -1,096 | 100,658 | |
| 4 | 7 | 37 | -2,002 | +2 | -2,000 | 98,658 | |
| ∑ | 13,3 | 73 | -3,1 | +4 | -3,096 | ||
| 3 | 4 | 98,658 | |||||
| 5 | 5,3 | 26 | 8,953 | +1 | +8,954 | 107,612 | |
| 6 | 5 | 28 | -5,092 | +1 | -5,091 | 102,521 | |
| 7 | 4,8 | 26 | -0,858 | 0 | -0,858 | 101,663 | |
| ∑ | 15,1 | 80 | 3,005 | +2 | +3,005 | ||
| 4 | 7 | 101,663 | |||||
| 8 | 7,4 | 33 | -1,038 | -3 | -1,041 | 100,622 | |
| Rp1 | 6,1 | 28 | 6,353 | -2 | +6,351 | 106,973 | |
| ∑ | 13,5 | 61 | 5,315 | -5 | +5,310 | ||
| 5 | 2 | 101,754 | |||||
| 9 | 7,8 | 41 | -3,186 | +6 | -3,180 | 98,574 | |
| 10 | 6,7 | 30 | 7,461 | +4 | +7,465 | 106,039 | |
| 11 | 6,5 | 38 | 15,617 | +5 | +15,622 | 121,661 | |
| 12 | 6,8 | 28 | -16,824 | +4 | -16,820 | 104,841 | |
| ∑ | 27,8 | 137 | 3,068 | +19 | +3,087 | ||
| 6 | 12 | 104,841 | |||||
| 13 | 7 | 36 | 7,299 | +1 | +7,300 | 112,141 | |
| ∑ | 7 | 36 | 7,299 | +1 | +7,300 | ||
| 7 | 13 | 112,141 | |||||
| 4 | 5,7 | 25 | -13,481 | -2 | -13,483 | 98,658 | |
| ∑ | 5,7 | 25 | -13,481 | -2 | -13,483 | ||
| 8 | 12 | 104,841 | |||||
| 14 | 10,6 | 54 | 4,811 | +10 | +4,821 | 109,662 | |
| ∑ | 10,6 | 54 | 4,811 | +10 | +4,821 | ||
| 9 | 14 | 109,662 | |||||
| 13 | 7,1 | 28 | 2,480 | -1 | +2,479 | 112,141 | |
| ∑ | 7,1 | 28 | 2,480 | -1 | +2,479 | ||
| 10 | 14 | 109,662 | |||||
| 15 | 5,4 | 29 | -7,899 | +6 | -7,893 | 101,769 | |
| 16 | 5,6 | 28 | 3,885 | +6 | +3,891 | 105,660 | |
| Rp2 | 6,5 | 32 | -5,536 | +8 | -5,528 | 100,132 | |
| ∑ | 17,5 | 89 | -9,55 | +20 | -9,530 | ||
| 11 | Rp2 | 100,132 | |||||
| 17 | 6,8 | 38 | 1,066 | -4 | +1,062 | 101,194 | |
| 7 | 6,8 | 25 | 0,472 | -3 | +0,469 | 101,663 | |
| ∑ | 13,6 | 63 | 1,538 | -7 | +1,531 | ||
В результате уравнивания я определила высоты всех точек. Для контроля использовала известные высоты Rp1=106.973 м, Rp2=100,132 м.
4.4 Оценка точности полученных результатов.
Далее я вычисляем среднюю квадратическую ошибку единицы веса поформуле
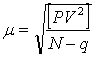 , (26),
, (26),
где 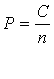 -
вес хода
-
вес хода
С – постоянное произвольное число, С=10
N – число станций в ходе
V – поправка в превышения на ход из уравнивания
N – число ходов
q – число узловых точек.
Вычислила среднюю квадратическую ошибку измеренного превышения на один километр хода по формулам
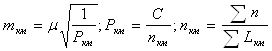 , (27),
, (27),
где nкм – число станций на 1 км хода
∑n – общее число станций по всем ходам
∑L – периметр всех ходов.
Вычислила среднюю квадратическую ошибку измеренного превышения на станции по формуле:
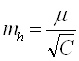 (28)
(28)
Таблица 12 - Схема вычислений при оценке точности
| обозначение хода | L, км | n | V | V² | P | PV² |
| 1 | 11,9 | 64 | -5,219 | 27,238 | 0,156 | 4,249 |
| 2 | 13,3 | 73 | -3,096 | 9,585 | 0,137 | 1,313 |
| 3 | 15,1 | 80 | 3,005 | 9,030 | 0,125 | 1,129 |
| 4 | 13,5 | 61 | 5,310 | 28,196 | 0,164 | 4,624 |
| 5 | 27,8 | 137 | 3,087 | 9,529 | 0,073 | 0,696 |
| 6 | 7 | 36 | 7,300 | 53,290 | 0,278 | 14,815 |
| 7 | 5,7 | 25 | -13,483 | 181,791 | 0,400 | 72,716 |
| 8 | 10,6 | 54 | 4,821 | 23,242 | 0,185 | 4,360 |
| 9 | 7,1 | 28 | 2,479 | 6,145 | 0,357 | 2,194 |
| 10 | 17,5 | 89 | -9,530 | 90,821 | 0,112 | 10,172 |
| 11 | 13,6 | 63 | 1,531 | 2,344 | 0,159 | 0,373 |
| ∑=143,1 | ∑=710 | 2,159 | ∑=116,581 |
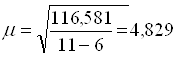
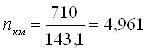
![]()
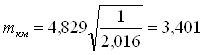
![]()
При решении этой задачи я освоила уравнивание ходов технического нивелирования способом полигонов профессора В.В.Попова. Узнала что такое «красные числа» и научилась распределять невязки пропорционально этим числам. По тому, что после решения этой задачи, у меня выполнились все необходимые контроли, я сделала вывод, что правильно усвоила методику уравнивания.
В данной курсовой работе обработаны и освоены результаты геодезических измерений в сетях сгущения методом прямой и обратной засечки, уравнены ходы полигонометрии 2 – го разряда, а также уравнены ходы нивелирования 4 класса способом полигонов профессора В.В.Попова.
В результате вычисления координат дополнительного пункта, определяемого прямой и обратной многократной засечками я получила следующие данные:
Прямая засечка:
- графический способ: Х=5328 м, Y=3045 м;
- аналитический способ: Х=5310,46 м, Y=3040,66 м.
Обратная засечка:
- графический способ: Х=6893 м, Y-3407 м ;
-аналитический способ: Х=6890,01 м, Y=3400,59 м.
Уравнивание ходов полигонометрии второго разряда, образующих одну узловую точку дало вероятнейшее значения координат по данным всех ходов: Хв=2346519,75 м, Yв=9474920,90 м.
Уравнивание ходов технического нивелирования способом полигонов профессора В.В. Попова получила высоты точек по ходам, по уравненным превышениям. Из проведенных вычислений и контроля получила высоты Rp=106,973 м1 и Rp2=100,132 м.
Список используемой литературы
1. Пархоменко Н.А лекции по дисциплине «Геодезия», 2005
2. Пархоменко Н.А., Седышев М.Е. «Методика математической обработки результатов геодезических измерений в сетях сгущения», Омск: ФГОУ ВПО ОмГАУ, 2004 – 24 с.
3. Маслов А.В., Гордеев А.В., Батраков Ю.Т. «Геодезия», 2005.