We have now discussed the data which the firm needs for its decision-making—the demand for its products and the cost of supplying them. But, even with this information, in order to determine what decisions are optimal it is still necessary to find out the businessman's aims. The decision which best serves one set of goals will not usually be appropriate for some other set of aims.

1. Alternative Objectives of the Firm

There is no simple method for determining the goals of the firm (or of its executives). One thing, however, is clear. Very often the last person to ask about any individual's motivation is the person himself (as the psychoanalysts have so clearly shown). In fact, it is common experience when interviewing executives to find that they will agree to every plausible goal about which they are asked. They say they want to maximize sales and also to maximize profits; that they wish, in the bargain, to minimize costs; and so on. Unfortunately, it is normally impossible to serve all of such a multiplicity of goals at once.

For example, suppose an advertising outlay of half a million dollars minimizes unit costs, an outlay of 1.2 million maximizes total profits, whereas an outlay of 1.8 million maximizes the firm's sales volume. We cannot have all three decisions at once. The firm must settle on one of the three objectives or some compromise among them.

Of course, the businessman is not the only one who suffers from the desire to pursue a number of incompatible objectives. It is all too easy to try to embrace at one time all of the attractive-sounding goals one can muster and difficult to reject any one of them. Even the most learned have suffered from this difficulty. It is precisely on these grounds that one great economist was led to remark that the much-discussed objective of the greatest good for the greatest number contains one "greatest" too many.

It is most frequently assumed in economic analysis that the firm is trying to maximize its total profits. However, there is no reason to believe that all businessmen pursue the same objectives. For example, a small firm which is run by its owner may seek to maximize the proprietor's free time subject to the constraint that his earnings exceed some minimum level, and, indeed, there have been cases of overworked businessmen who, on medical advice, have turned down profitable business opportunities.

It has also been suggested, on the basis of some observation, that firms often seek to maximize the money value of their sales (their total revenue) subject to a constraint that their profits do not fall short of some minimum level which is just on the borderline of acceptability. That is, so long as profits are at a satisfactory level, management will devote the bulk of its energy and resources to the expansion of sales. Such a goal may, perhaps, be explained by the businessman's desire to maintain his competitive position, which is partly dependent on the sheer size of his enterprise, or it may be a matter of the interests of management (as distinguished from shareholders), since management's salaries may be related more closely to the size of the firm's operations than to its profits, or it may simply be a matter of prestige.

In any event, though they may help him to formulate his own aims and sometimes be able to show him that more ambitious goals are possible and relevant, it is not the job of the operations researcher or the economist to tell the businessman what his goals should be. Management's aims must be taken to be whatever they are, and the job of the analyst is to find the conclusions which follow from these objectives—that is, to describe what businessmen do to achieve these goals, and perhaps to prescribe methods for pursuing them more efficiently.

The major point, both in economic analysis and in operations-research investigation of business problems, is that the nature of the firm's objectives cannot be assumed in advance. It is important to determine the nature of the firm's objectives before proceeding to the formal model-building and the computations based on it. As is obviously to be expected, many of the conclusions of the analysis will vary with the choice of objective function. However, as some of the later discussion in this chapter will show, a change in objectives can, sometimes surprisingly, leave some significant relationships invariant. Where this is true, it is very convenient to find it out in advance before embarking on the investigation of a specific problem. For if there are some problems for which the optimum decision will be the same, no matter which of a number of objectives the firm happens to adopt, it is legitimate to avoid altogether the difficult job of determining company goals before undertaking an analysis.

2. The Profit-Maximizing Firm

Let us first examine some of the conventional theory of the profit-maximizing firm. In the chapter on the differential calculus, the basic marginal condition for profit maximization was derived as an illustration. Let us now rederive this marginal-cost-equals-marginal-revenue condition with the aid of a verbal and a geometric argument.

The proposition is that no firm can be earning maximum profits unless its marginal cost and its marginal revenue are (at least approximately) equal, i.e., unless an additional unit of output will bring in as much money as it costs to produce, so that its marginal profitability is zero.

It is easy to show why this must be so. Suppose a firm is producing 200,000 units of some item, x, and that at that output level, the marginal revenue from x production is $1.10 whereas its marginal cost is only 96 cents. Additional units of x will, therefore, each bring the firm some 14 cents = $1.10 — 0.96 more than they cost, and so the firm cannot be maximizing its profits by sticking to its 200,000 production level. Similarly, if the marginal cost of x exceeds its marginal revenue, the firm cannot be maximizing its profits, for it is neglecting to take advantage of its opportunity to save money—by reducing its output it would reduce its income, but it would reduce its costs by an even greater amount.

We can also derive the marginal-cost-equals-marginal-revenue proposition with the aid of Figure 1. At any output, OQ, total revenue is represented by the area OQPR under the marginal revenue curve (see Rule 9 of Chapter 3). Similarly, total cost is represented by the area OQKC immediately below the marginal cost curve. Total profit, which is the difference between total revenue and total cost is, therefore, represented by the difference between the two areas—that is, total profits are given by the lightly shaded area TKP minus the small, heavily shaded area, RTC. Now, it is clear that from point Q a move to the right will increase the size of the profit area TKP. In fact, only at output OQm will this area have reached its maximum size—profits will encompass the entire area TKMP.

OUTPUT

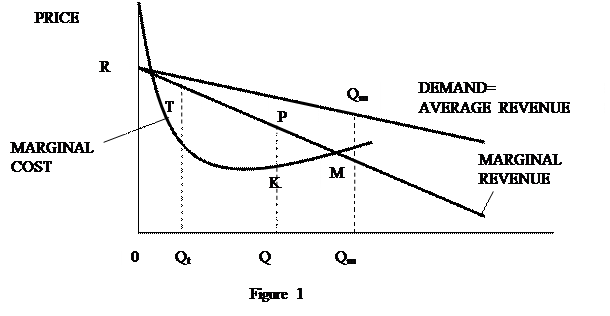
But at output OQm marginal cost equals marginal revenue—indeed, it is the crossing of the marginal cost and marginal revenue curves at that point which prevents further moves to the right (further output increases) from adding still more to the total profit area. Thus, we have once again established that at the point of maximum profits, marginal costs and marginal revenues must be equal.

Before leaving the discussion of this proposition, it is well to distinguish explicitly between it and its invalid converse. It is not generally true that any output level at which marginal cost and marginal revenue happen to be equal (i.e., where marginal profit is zero) will be a profit-maximizing level. There may be several levels of production at which marginal cost and marginal revenue are equal, and some of these output quantities may be far from advantageous for the firm. In Figure 1 this condition is satisfied at output OQt as well as at OQm. But at OQt the firm obtains only the net loss (negative profit) represented by heavily shaded area RTC. A move in either direction from point Qt will help the firm either by reducing its costs more than it cuts its revenues (a move to the left) or by adding to its revenues more than to its costs. Output OQt is thus a point of minimum profits even though it meets the marginal profit-maximization condition, "marginal revenue equals marginal cost."

This peculiar result is explained by recalling that the condition, "marginal profitability equals zero," implies only that neither a small increase nor a small decrease in quantity will add to profits. In other words, it means that we are at an output at which the total profit curve (not shown) is level—going neither uphill nor downhill. But while the top of a hill (the maximum profit output) is such a level spot, plateaus and valleys (minimum profit outputs) also have the same characteristic—they are level. That is, they are points of zero marginal profit, where marginal cost equals marginal revenue.

We conclude that while at a profit-maximizing output marginal cost must equal marginal revenue, the converse is not correct—it is not true that at an output at which marginal cost equals marginal revenue the firm can be sure of maximizing its profits.

3. Application: Pricing and Cost Changes

The preceding theorem permits us to make a number of predictions about the behavior of the profit-maximizing firm and to set up some normative "operations research" rules for its operation. We can determine not only the optimal output, but also the profit-maximizing price with the aid of the demand curve for the product of the firm. For, given the optimal output, we can find out from the demand curve what price will permit the company to sell this quantity, and that is necessarily the optimal price. In Figure 1, where the optimal output is OQm we see that the corresponding price is QmPm where point Pm is the point on the demand curve above Qm (note that Pm is not the point of intersection of the marginal cost and the marginal revenue curves).

It was shown in the last section of Chapter 4 how our theorem can also enable us to predict the effect of a change in tax rates or some other change in cost on the firm's output and pricing. We need merely determine how this change shifts the marginal cost curve to find the new profit-maximizing price-output combination by finding the new point of intersection of the marginal cost and marginal revenue curves. Let us recall one particular result for use later in this chapter—the theorem about the effects of a change in fixed costs. It will be remembered that a change in fixed costs never has any effect on the firm's marginal cost curve because marginal fixed cost is always zero (by definition, an additional unit of output adds nothing to fixed costs). Hence, if the profit-maximizing firm's rents, its total assessed taxes, or some other fixed cost increases, there will be no change in the output-price level at which its marginal cost equals its marginal revenue. In other words, the profit-maximizing firm will make no price or output changes in response to any increase or decrease in its fixed costs! This rather unexpected result is certainly not in accord with common business practice and requires some further comment which will be supplied presently.

4. Extension: Multiple Products and Inputs

The firm's output decisions- are normally more complicated, even in principle, than the preceding decisions suggest. Almost all companies produce a variety of products and these various commodities typically compete for the firm's investment funds and its productive capacity. At any given time there are limits to what the company can produce, and often, if it decides to increase its production of product x, this must be done at the expense of product y. In other words, such a company cannot simply expand the output of x to its optimum level without taking into account the effects of this decision on the output of y.

For a profit-maximizing decision which takes both commodities into account we have a marginal rule which is a special case of Rule 2 of Chapter 3:

Any limited input (including investment funds) should be allocated between the two outputs x and у in such a way that the marginal profit yield of the input, i, in the production of x equals the marginal profit yield of the input in the production of y.

If the condition is violated the firm cannot be maximizing its profits, because the firm can add to its earnings simply by shifting some of г out of the product where it obtains the lower return and into the manufacture of the other.

Stated another way, this last theorem asserts that if the firm is maximizing its profits, a reduction in its output of x by an amount which is worth, say, $5, should release just exactly enough productive capacity, C, to permit the output of у to be increased $5 worth. For this means that the marginal return of the released capacity is exactly the same in the production of either x or y, which is what the previous version of this rule asserted.3

Still another version of this result is worth describing: Suppose the price of each product is fixed and independent of output levels. Then we require that the marginal cost of each output be proportionate to its price, i.e., that 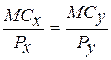where Px and MCX are, respectively, the price and the marginal cost of x, etc.

In this discussion we have considered only the output decisions of a profit-maximizing firm. Of course, the firm has other decisions to make. In particular, it must decide on the amounts of its inputs including its marketing inputs (advertising, sales force, etc.). There are similar rules for these decisions, as discussed in Chapter 11 and in Chapter 17, Section 6. The main result here is that profit maximization requires for any inputs г and j

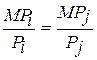where MPt represents the marginal profit contribution of input г and Pi is its price, etc.

Having discussed the consequences of profit maximization, let us see now what difference it makes if the firm adopts an alternative objective, one to which we have already alluded — the maximization of the value of its sales (total revenue) under the requirement that the firm's profits not fall short of some given minimum level.

5. Price-Output Determination: Sales Maximization

Saks maximization under a profit constraint does not mean an attempt to obtain the largest possible physical volume (which is hardly easy to define in the modern multi-product firm). Rather, it refers to maximization of total revenue (dollar sales) which, to the businessman, is the obvious measure of the amount he has sold. Maximum sales in this sense need not require very large physical outputs. To take an extreme case, at a zero price physical volume may be high but dollar sales volume will be zero. There will normally be a well-determined output level which maximizes dollar sales. This level can ordinarily be fixed with the aid of the well-known rule that maximum revenue will be obtained only at an output at which the elasticity of demand is unity, i.e., at which marginal revenue is zero. This is the condition which replaces the "marginal cost equals marginal revenue" profit-maximizing rule.

But this rule does not take into account the profit constraint. That is, if at the revenue-maximizing output the firm does, in fact, earn enough or more than enough profits to keep its stockholders satisfied then it will want to produce the sales-maximizing quantity. But if at this output profits are too low, the firm's output must be changed to a level which, though it fails to maximize sales, .does meet the profit requirement.

We see, then, that two types of equilibrium appear to be possible: one in which the profit constraint does not provide an effective barrier to sales maximization, and one in which it does. This is illustrated in Figure 2, which shows the firm's total revenue, cost, and profit curves as indicated.

The profit- and sales-maximizing outputs are, respectively, OQP and OQ,. Now if, for example, the minimum required profit level is OP\, then the sales-maximizing output OQ, will provide plenty of profit, and that is the amount it will pay the sales maximizer to produce.

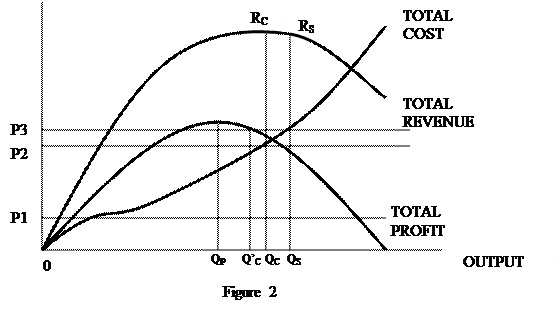
His selling price will then be set at Q,R,/OQ,. But if the producer's required profit level is OP2, output OQ,, which yields insufficient profit, clearly will not do. Instead, his output will be reduced to level OQC, which is just compatible with his profit constraint.

It will be argued presently that in fact only equilibrium points in which the constraint is effective (OQC rather than OQ,) can normally be expected to occur when other decisions of the firm are taken into account.

The profit-maximizing output, OQP, will usually be smaller than the one which yields either type of sales maximum, OQ, or OQC. This can be proved with the aid of the standard rule that at the, point of maximum profit marginal cost must equal marginal revenue. For marginal cost is normally a positive number (we can't usually produce more of a good for nothing). Hence marginal revenue will also be positive when profits are at a maximum, i.e., a further increase in output will increase total sales (revenue). Therefore, if at the point of maximum profit the firm earns more profit than the required minimum, it will pay the sales maximizer to lower his price and increase his physical output.

2. Перевод текста с языка оригинала

Фирма и её цели

Мы обсудили данные, которые необходимы фирме для принятия решений – спрос на её продукцию и стоимость продукции, предлагаемой ей. Но, даже имея эту информацию, чтобы определить, какие решения оптимальны, необходимо определить цели фирмы.

1. Альтернативные цели фирмы

Нет простого метода определения целей фирмы (или её исполнителей). Однако, одно ясно. Очень часто последний, кого спрашивают о некоторой индивидуальной мотивации, оказывается сам человек (как показали психоаналитики). В действительности, это простой способ, когда интервьюируются исполнители для того, чтобы определить, будут ли они согласны с каждой правдоподобной целью, о которой их спрашивают. Они отвечают, что хотят максимизировать продажи, а также прибыли, что они желают при заключении выгодной сделки минимизировать издержки, и тому подобное. К сожалению, в нормальных условиях невозможно удовлетворить все множество целей одновременно.

Например, предположим, что издержки на рекламу составляют миллион долларов минимизируют общие расходы, издержки в 1,2 млн долларов максимизируют совокупную прибыль, тогда как издержки в 1, 8 млн долларов максимизируют объём продаж фирмы. Мы не можем иметь три решения одновременно. Фирма должна одну цель из трех или найти некоторый компромисс среди них.

Конечно, предприниматель не последний, кто страдает от желания заниматься множеством несовместимых целей. Слишком трудно пытаться охватить одновременно все звучащие привлекательными цели, каждая может приниматься в рассмотрение и трудно отказаться от любой из них. Даже многие ученые сталкиваются с этой трудностью. Точно на этих основаниях один великий экономист высказался, что много обсуждаемая цель из великого множества хороших целей содержит слишком много «великого».

Очень часто в экономическом анализе предполагается, что фирма пытается максимизировать свою прибыль. Однако из этого не следует, что все бизнесмены преследуют подобные цели. Например, небольшая фирма, руководимая своим владельцем, может пытаться максимизировать свободное время владельца, чтобы предотвратить ситуацию, когда его заработок превысит некоторый минимальный уровень, и, в действительности, были случаи перегруженных работой предпринимателей, которые по медицинским советам, уменьшали прибыльные возможности бизнеса.

Также предполагается, на основе некоторого исследования, что фирмы часто пытаются максимизировать объём продаж (совокупный годовой доход) для предупреждения того, что прибыль упадет ниже некоторого минимального уровня, который является границей приемлемости. Таким образом, пока прибыль находится на удовлетворительном уровне, управление может передать часть энергии и ресурсов на увеличение продаж. Подобная цель, возможно, может быть объяснена тем, что бизнесмены хотят сохранить конкурентную позицию, которая отчасти зависит от размера предприятия или может быть предметом интересов управления (в зависимости от акционеров) до тех пор, пока заработки управления могут быть отнесены более закрыто к величине операций фирмы, чем к её прибылям, или может быть просто предметом престижа.

В любом случае, хотя они могут помочь ему сформулировать свои собственные цели и иногда быть способны показать ему, что более амбициозные цели возможны и уместны, не является работой исследователя операций или экономиста сообщить бизнесмену, какие должны быть цели. Цели управления должны быть приняты, какими бы они ни были, и работа аналитика состоит в определении выводов, которые следуют из целей, определить, что бизнесмен должен делать для достижения своих целей, и , возможно, описать методы для следования им более эффективно.

Основная точка соприкосновения, как в экономическом анализе, так и в исследовании операций проблем бизнеса, состоит в том, что цели фирмы не могут быть приняты в большинстве. Важно определить природу целей фирмы до того, как приступить к формальному моделированию и вычислениям. Очевидно ожидать, что множество выводов анализа будут изменяться при выборе функции цели. Однако, как будет позже показано в этой главе, что выбор целей может иногда к удивлению привести к значительным различиям. Что верно, удобно определить в большинстве случаев до того, как погрузиться в исследование специфической проблемы. Поэтому, если есть некоторые проблемы, оптимальное решение для которых одно и то же, не факт, что большинство целей фирмы принимаются, законно избегать до начала анализа трудной работы при определении целей компании.

2. Фирма, максимизирующая прибыль.

Для начала исследуем некоторую имеющуюся теорию о фирме, максимизирующей прибыль. В главе, посвященной дифференциальным уравнениям, основное маржинальное условие для максимизации прибыли было показано на иллюстрации. Теперь рассмотрим это условие («предельные издержки равняются предельному доходу») с помощью словесного и геометрического аргументов.

Предположение, что фирма не может заработать максимальную прибыль, если её предельные расходы не равны предельному доходу (или, по крайней мере, близки), т.е. если дополнительная единица выпуска не принесёт столько же дохода, сколько израсходовано при производстве, таким образом, предельная прибыльность равна нулю.

Легко показать, почему так должно быть. Предположим, что фирма, производящая 200000 единиц некоторого продукта x и при таком уровне производства предельный доход составит 1.1 $, тогда как её маржинальные издержки составят только 96 центов. Каждая дополнительная единица x принесет фирме 14 центов (= 1,10-0,96); это больше, чем фирма израсходовала, и таким образом, фирма не может максимизировать свои прибыли, пренебрегая возможностью сохранить деньги – снижая свой объем производства, это снизит его доход, но это же снизит расходы, даже в большем объеме.

Также предположение, что «предельные издержки равняются предельному доходу», можно показать с помощью рисунка 1.

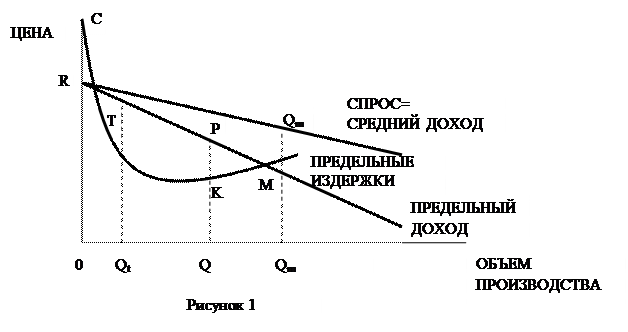
При любом выпуске OQ совокупный доход представлен площадью OQPR под кривой предельного дохода. Подобно этому, общие расходы представлены площадью OQKC под кривой предельных издержек. Общая прибыль, которая есть разница между общим доходом и общими издержками, таким образом представлена разницей между двумя площадями – общая прибыль показана светло закрашенной площадью TKP минус небольшая, сильно закрашенная площадь RTC. Теперь ясно, что из точки Q движением вправо увеличивается размер площади прибыли TKP. В действительности, только при выпуске m эта площадь достигнет своего максимального размера – прибыль будет занимать площадь TKMP. Но при выпуске m предельные издержки равны предельному доходу – на самом деле это пересечение в этой точке кривых предельных издержек и предельного дохода, которое предотвращается дальнейшим движением вправо (дальнейшее увеличение производства) при ещё большем увеличении площади совокупных прибылей. Таким образом, предельные издержки должны равняться предельному доходу.

Прежде чем оставить обсуждение этого предположения, хорошо было бы точно различить его и его толкование. Не совсем верно, что любой уровень объема производства, при котором предельные издержки равны предельному доходу (т.е. прибыль равна нулю) будет уровнем максимизации прибыли. Могут быть уровни производства продукции, при которых предельные издержки равны предельному доходу, и некоторые из них могут быть далеки от выгодных для фирмы. На рисунке 1 это условие подтверждается при выпуске OQt также, как и при выпуске m. Но при выпуске OQt фирма получает только чистые убытки (отрицательную прибыль), представленную сильно закрашенной площадью RTC. Движения в любом направлении от точки Q помогут фирме либо снижением издержек большим, чем уменьшением доходов (перемещения влево), либо повышением доходов большим, чем издержек. Объем производства OQt таким образом является точкой минимума прибыли, даже если он удовлетворяет условию максимизации прибыли – «предельные издержки равняются предельному доходу».

Этот необычный результат объясняется отменой условия, что предельная прибыльность равна нулю, означающего только то, что ни малое увеличение, ни малое уменьшение объема производства не увеличит прибыли. Другими словами, это означает, что мы при объеме производства, при котором кривая общей прибыли (на рисунке не показана) есть прямая, не двигаемся ни вверх, ни вниз. Но до тех пор, пока вершина кривой (объем производства максимальной прибыли) есть точка уровня, «плато и долины» (объем производства минимальной прибыли) также имеют характеристики – они будут прямыми. Это есть точки нулевой предельной прибыли, где предельные издержки равны предельному доходу.

Делаем заключение, что вывод о том, что при объеме производства, максимизирующего прибыль, предельные издержки равны предельному доходу, неверен – неверно то, что при выпуске, при котором предельные издержки равны предельному доходу, фирма будет точно максимизировать прибыль.

3. Приложение: Ценообразование и изменение издержек

Предыдущая теорема позволяет нам сделать предположения о поведении фирмы, максимизирующей прибыль, и установить некоторые нормативные правила исследования операций для её действий. Мы можем определить не только оптимальный объем производства, но также цену максимизации прибыли с помощью кривой спроса для произвольного продукта фирмы. Для данного оптимального выпуска мы можем определить по кривой спроса, какая цена позволит компании продать выпущенное количество продукции. На рисунке 1, где оптимальный объем производства есть m, мы видим, что ему соответствует цена QmPm , где точка Pm является точкой на кривой спроса, соответствующей точке Qm (точка Pm не является точкой пересечения кривых предельных издержек и предельного дохода).

В предыдущем разделе главы было показано, как наша теорема может также предсказать эффект изменения налоговых ставок или некоторых других изменений в расходах фирмы или ценообразовании. Мы можем просто определить, как перемещения по кривой предельных издержек определят новую комбинацию значений цены-выпуска, максимизирующих прибыль, путем определения новой точки пересечения кривых предельных издержек и дохода. Отменим полученный особый результат для использования его позже в этой главе – теоремы об эффектах при изменении постоянных издержек. Напомним, что изменение постоянных издержек никогда не ведет к изменению кривой предельных издержек фирмы, потому что предельные постоянные издержки всегда равны нулю (по определению, что дополнительная единица производства не увеличивает постоянные издержки). Отсюда следует, если арендная плата фирмы, максимизирующей прибыль, её налоги или некоторые другие постоянные издержки увеличиваются, тогда не будет изменений значений цены-выпуска, при которых предельные издержки и предельный доход равны. Другими словами, фирма, максимизирующая прибыль, не изменит цены и выпуска, чтобы соответствовать некоторым увеличению или уменьшению в их постоянных издержках! Этот довольно неожиданный результат не соответствует обычной деловой практике и требует некоторого дальнейшего пояснения, которое будет сейчас представлено.

4. Продолжение: Разнообразие продукции и ресурсов.

Решения фирмы об объемах производства в действительности более сложные, даже в принципе, чем предложенные в предыдущем решения. Почти все компании производят множество продуктов, и эти разнообразные товары типично конкурируют за капитал фирмы и его производственную мощность. В любой заданный момент времени существуют ограничения, что фирма может производить, и часто, если она решает увеличить объем производства продукта x, увеличение должно быть предпринято и в отношении продукта y.

Для решения по максимизации прибыли, которое принимает в расчет все товары, имеется маржинальное правило, которое является специальным случаем правила 2 главы 3:

Любой ограниченный ресурс (в том числе и капитал)должен быть распределен между выпуском 2 продуктов x и y таким образом, чтобы предельная прибыль ресурса i при производстве продукта x равнялась предельной прибыли ресурса при производстве продукта y.

Если условие нарушается, фирма не может максимизировать прибыль, потому что она может увеличить свой доход, просто изменяя значение i одного продукта, это приводит к снижению дохода и при производстве другого продукта.

При изложении другого подхода последняя теорема доказывает, что если фирма максимизирует прибыль, уменьшение выпуска продукта x в размере, скажем, $5 увеличит точно производственную мощность, С, и позволит увеличить выпуск продукции y также на $5, Это означает, что предельный доход увеличенной мощности будет таким же, как при производстве продукта x, так и при производстве продукта y, что предыдущая версия этого правила и доказала.

Ещё одна версия этого результата гласит: Предположим, цена каждого продукта постоянна и не зависит от объёмов производства. Тогда требуется, чтобы предельные издержки при каждом выпуске будут пропорциональны его цене, т.е. , где Рх и соответственно цена и маржинальные издержки продукта х и т.д.

При этом обсуждении мы учитывали только решения по выпуску продукции фирмы, максимизирующей прибыль. Конечно, фирма может принять другое решение. В особенности это должно решаться в отношении размеров ресурсов, включая маркетинговые расходы (реклама, увеличение продаж и т.д.). Существуют правила для таких решений, как обсуждалось в главе 11 и главе 17, разделе 6. Главный результат здесь состоит в том, что максимизация прибыли требует для любых ресурсов выполнения условия , где означает в клад ресурса i в предельную прибыль, а - его цену.

Обсуждая выводы о максимизации прибыли, теперь видим, какое может быть различие, если фирма принимает альтернативную цель, на которое мы уже ссылались, - максимизацию продаж (общего дохода)при требовании, что прибыль фирмы не упадет ниже некоторого заданного минимального уровня.

5. Определение значений цены-выпуска: Максимизация продаж.

Максимизация продаж при сдерживании прибыли не означает попытку достичь наибольшего возможного физического объема (который нелегко определить в современной мультипродуктовой фирме). Скорее это относится к максимизации совокупного дохода (продаж), который для бизнесмена является величиной продукции, которую оно продал. Максимум продаж в этом смысле не требует очень больших объемов выпуска. Если взять крайний случай, при нулевой цене физический объем может быть высоким, но объем продаж будет нулевым. Обычно определяется объем производства, который обеспечивает максимум продаж. Этот объем может обычно быть зафиксирован с помощью известного правила, которое говорит, что максимальный доход достигается только при выпуске, при котом эластичность спроса одинакова, т.е., при котором маржинальный доход равен нулю. Это условие заменяет правило максимизации прибыли – «предельные издержки равны предельному доходу».

Но это правило не принимает в расчет сдерживание прибыли. Т.е., если при выпуске, максимизирующем доход, фирма, в действительности, достаточно или более чем достаточно прибыли, для того, чтобы удовлетворить требования акционеров, тогда она захочет производить количество продукции, при котором продажи максимальны. Но если при таком выпуске прибыль слишком мала, объем производства фирмы должен быть изменен до уровня, при котором, хотя продажи максимизируются, удовлетворяется требование нормы прибыли.

Мы видим, что возможны 2 типа равновесия: первый, при котором сдерживание прибыли не обеспечивает эффективного барьера для максимизации продаж, и второй – при котором обеспечивает. Это проиллюстрировано на рисунке 2, который показывает кривые общего дохода фирмы, издержек и прибыли.

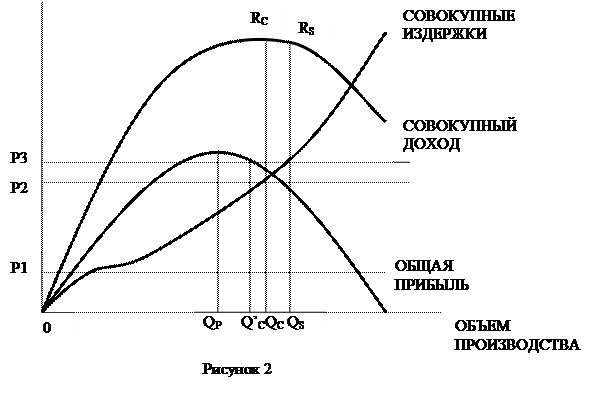
Объемы производства, при котором обеспечивается максимум прибыли и продаж, - соответственно р и s. Например, если минимальный требуемый уровень прибыли – OP1, тогда выпуск, максимизирующий продажи, s обеспечивает избыток прибыли и это есть величина, которую заплатит максимизатор прибыли при производстве. Его цена продажи тогда будет равна . Но если требуемый уровень прибыли производителя равен OP2 , выпуск s, который не обеспечивает достаточно прибыли, не будет равен этому соотношению. Место этого, выпуск будет уменьшен до уровня с , который совместим со сдерживанием прибыли.

Будет доказано, что в действительности только точки равновесия, в которых сдерживание эффективное, могут быть ожидаемы, когда другие решения фирмы приняты в расчет. Выпуск максимума прибыли р обычно будет меньше, чем какой-либо другой, который является либо s, либо с. Это может быть доказано с помощью стандартного правила, которое говорит, что в точке максимума прибыли предельные издержки должны равняться предельному доходу. Так как предельные издержки обычно положительная величина (мы не можем производить из ничего). Отсюда, предельный доход будет тоже положительным, когда прибыль максимальная, т.е. дальнейшее увеличение объема производства увеличит совокупный объем продаж (доход). Поэтому, если в точке максимума прибыли фирма получает больше прибыли, чем требуемый минимум, максимизатор продаж платит меньше цены товара и увеличит физический объем продаж.

3. Словарь экономических терминов по специальности

№ п/п	Исходный текст	Перевод
1	acceptance sampling	приемлемая выборка
2	account	счет
3	account balance	сальдо по счету (остаток по счету)
4	accounting estimate	оценочное значение
5	accounting income	учетная прибыль
6	accounting model	учетная модель, бухгалтерская модель
7	accounting system	система бухгалтерского учета
8	accrual basis	метод начисления
9	accruals concept	принцип начисления
10	accrued revenue	начисленная выручка
11	accumulated depreciation	накопленная амортизация
12	accumulated loss	накопленный убыток
13	accumulated profit	накопленная прибыль
14	acquiree	приобретенная, приобретаемая компания
15	acquisition	приобретение, покупка
16	acquisition accounting	учет приобретения
17	actively managed funds	активно управляемые фонды
18	actuarial assumptions	актуарные допущения
19	actuarial gains and losses	актуарные прибыли и убытки
20	actuarial valuation method	метод актуарной оценки
21	adjusted trial balance	скорректированный проверочный / пробный баланс
22	advantageous	выгодный
23	adverse opinion	отрицательное мнение
24	advertising	рекламный
25	advisor	консультант
26	affiliate	дочернее общество
27	aggregation	обобщение, суммирование
28	aggressive investment strategy	агрессивная инвестиционная стратегия
29	agreed upon procedures	согласованные процедуры
30	agricultural activity	сельскохозяйственная деятельность
31	allocation	размещение, распределение
32	allowance	оценочный резерв
33	altitud	высота
34	amortisation	амортизация нематериальных активов
35	amortisation period	срок амортизации
36	analysis	анализ
37	angle	угол наклона
38	annual	ежегодный
39	anomalous error	нетиповая ошибка
40	apparatus	прибор, аппаратура
41	application control	прикладные средства контроля
42	apply	применять, прилагать
43	appraisal (of mineral reserves)	оценка (запасов полезных ископаемых)
44	appraised value	оценочная стоимость
45	appraisement	оценка, оценивать
46	appropriateness relevance	уместность
47	appropriation accounting	учет путем распределения
48	approximately	приблизительно
49	arbitrary	произвольный
50	arc	дуга
51	area of interest	перспективная территория
52	arithmetic	арифметический
53	arm's length transaction	сделка между независимыми друг от друга сторонами
54	arrangement	классификация
55	array	массив
56	asking price	цена предложения
57	assertion	утверждение
58	assess	определять размер, сумму штрафа, облагать налогом
59	asset	активы
60	asset allocation fund	фонд распределения активов
61	assignment	ассигнование
62	assistance	помощь, содействие
63	associate	ассоциированная компания
64	assurance service	услуги по предоставлению финансовой информации
65	assured	страхователь
66	attendance	присутствие
67	authorisation	разрешение
68	automatic investment plan	автоматический инвестиционный план
69	automation	автоматизация
70	available-for-sale financial assets	финансовые активы, имеющиеся в наличии для продажи
71	average annual return	средняя годовая доходность
72	average effective duration	средняя фактическая (эффективная) дюрация
73	average revenue	средний доход
74	axiom	аксиома
75	axis	ось
76	backer	поручитель, индоссант
77	backlog	задолженность
78	backwarder	мелкий производитель
79	bail	залог, поручительство
80	bailor	депонент
81	balance	баланс
82	balance sheet liability method	метод обязательств по балансу
83	balanced fund	сбалансированный фонд
84	balanced investment strategy	сбалансированная инвестиционная стратегия
85	balancing item	статья, по которой выводится остаток
86	bank	банк
87	bank-rate	учетная ставка банка
88	bank-stock	акционергый капитал банка
89	bargain	сделка, соглашение, договор о покупке, выгодная покупка
90	bargainer	участник сделки, торговец
91	barrels-of-oil equivalent	эквивалент в баррелях нефти
92	base stock	метод базовых запасов
93	benchmark	основной подход
94	benchmark treatment	основной порядок учета
95	benefit	польза, приносить пользу
96	bias	уклон, наклон
97	bid up	набавлять цену
98	bilaterial monopoly	двусторонняя монополия
99	bill of lading	накладная, коносамент
100	binding sale agreement	соглашение о продаже, имеющее обязательную силу
101	bonanza	доходное предприятие
102	bond funds	облигационные фонды
103	bonds payable	облигации к оплате
104	bonus payments	премиальные
105	bonus-job	сдельная работа
106	borrowing costs	затраты по займам
107	bottom-up investing	инвестирование на базе корпоративных финансовых результатов
108	bound	граница
109	branch	отрасль
110	break-up	разорение, распад
111	break-up basis	метод учета в условиях срочной реализации имущества
112	bribe	взятка, подкуп
113	broker	брокер, маклер
114	budget	бюджет, финансовая смета
115	budgetary funds	бюджетные средства
116	bulk	масса, объем
117	business combination	объединение компаний
118	business segment	хозяйственный сегмент
119	businessman	бизнесмен, предприниматель
120	by-product	побочный продукт
121	cadre	кадры
122	calculate	вычислять, исчислять
123	calendar-year total returns	общая доходность за календарный год
124	call option	опцион покупателя
125	campaign	кампания, проводить кампанию
126	capability to change	способность к изменению
127	capacity bottlenecks	нехватка мощностей
128	capital	капитал
129	capital gains	прирост капитала
130	capital maintenance	поддержание капитала
131	capital-intensive	капиталоёмкий
132	capitalisation	капитализация
133	cargo	груз корабля
134	carrying amount	балансовая стоимость
135	carrying amount (book value)	учетная стоимость (балансовая стоимость)
136	cash equivalents	эквиваленты денежных средств
137	cash flows	движение денежных средств
138	cash inflow	поступление денежных средств
139	cash/equivalent	наличные/эквиваленты наличности
140	catastrophe (cat) provisions	резервы на катастрофы (рк)
141	catastrophe bonds	облигации, связанные с риском катастроф
142	category rating	рейтинг фонда в рамках категории
143	category risk	ранг риска фонда в рамках категории
144	ceding insurer	перестрахователь, цедент (передающая страховая компания)
145	centralize	централизовать
146	centralized planning	централизованное планирование
147	chaos	хаос
148	charges	расходы, издержки
149	chattel	движимое имущество
150	cheap	дешевый
151	check register	реестр чеков
152	chief audit executive	руководитель внутреннего аудита
153	claim	требование
154	claim processing expenses	расходы по обработке требований о возмещении ущерба
155	claims payable	страховое возмещение к оплате
156	class of assets	класс активов
157	client's account	счет клиента
158	closed-end funds	"закрытые" инвестиционные фонды
159	closing rate	валютный курс на отчетную дату
160	closing rate method	метод курса на отчетную дату
161	collusion	тайное соглашение
162	comfort letter	рекомендательное письмо
163	commitent	обязательство
164	commodity	предмет потребления, продукт, товар
165	communication	представление отчетности, информации
166	comparability	сопоставимость
167	comparable financial statements	сопоставимая финансовая отчетность
168	comparatives	относительные показатели
169	comparison	сравнение
170	competition	конкуренция
171	compilation	подготовка информации
172	complementary goods	товары-дополнители
173	completeness	полнота
174	compound instrument	сложный финансовый инструмент
175	computation	расчет, вычисление
176	computation	подсчет
177	concave region	вогнутая область
178	confine	пределы, граница
179	conservatism	принцип консерватизма
180	considerable	значительный
181	consistency	последовательность
182	consolidation	сведение, консолидация
183	constrain	ограничения
184	constraint equation	уравнение-ограничение
185	construction	строительство
186	constructive obligation	обязательство, вытекающее из практики
187	contingency	условные события
188	contingent deferred sales charge	комиссия на продажу, зависящая от срока инвестиций
189	contingent gain	условный доход
190	contingent loss	условный убыток
191	contingent rent	условная арендная плата
192	continuing auditor	постоянный аудитор
193	contract	договор
194	contradiction	противоречие
195	contribution	вклад, взнос, сотрудничество
196	control	контроль
197	control procedure	процедура контроля
198	control process	процесс контроля
199	control risk	риск системы контроля
200	controller	проверяющий
201	converse	обратная теорема
202	convex region	выпуклая область
203	conveyance	передача прав собственности (на месторождение полезных ископаемых)
204	corner maximum	угловой максимум
205	corporation	корпорация, объединение, акционерное общество
206	corresponding figures	соответствующие показатели
207	cost of an acquisition	первоначальная стоимость приобретения
208	cost of goods purchased	фактическая стоимость купленных товаров
209	cost of inventories	себестоимость запасов
210	cost of sales	себестоимость продаж
211	cost of services	стоимость услуг
212	count	считать, итог, счёт
213	credit	кредит
214	credit risk	кредитный риск
215	crop failure	неурожай
216	cross selling	продажа одним и тем же страхователям различных страховых продуктов
217	current cost approach	подход, основанный на текущих затратах
218	current cost method	метод учета по текущим затратам
219	current recovery value	текущая восстановительная стоимость
220	current service cost	стоимость текущих услуг
221	current value	текущая стоимость
222	curtailment	секвестр, ограничение, уменьшение
223	curve	кривая
224	custody	ответственное хранение
225	customer	потребитель
226	customhouse	таможня
227	damage	убыток
228	damaged inventories	поврежденные запасы
229	date of acquisition	дата приобретения
230	datum	исходный факт, данная величина
231	dealing securities	спекулятивные ценные бумаги
232	debit	дебет
233	debtor	дебитор
234	decline	падение, снижение, упадок
235	declining balance method	метод уменьшаемого остатка (амортизация)
236	decomposition (of the contract)	расчленение (договора)
237	decrease	снижение, уменьшение
238	decrease in long-term loan	уменьшение долгосрочных займов, кредитов
239	deduce	выводить (заключение, следствие, теорему)
240	deduct	вычитать, отнимать
241	deductible temporary difference	вычитаемая временная разница
242	deferral and matching	отсрочка и соответствие (соотнесение)
243	deferral method	метод отсрочки
244	deferral model	модель с отсроченной премией
245	deferred compensation	отсроченная компенсация
246	deferred income	отложенная прибыль
247	deferred payment	отсроченный платеж
248	deferred payment terms	условия отсрочки платежа
249	deferred revenue	отложенная выручка
250	deferred tax asset	отложенные налоговые требования
251	deferred tax liabilities	отложенные налоговые обязательства
252	deficit	дефицит
253	defined benefit obligation	обязательство по пенсионному плану с установленными выплатами
254	defined benefit plan	пенсионный план с установленными выплатами
255	defined contribution plan	пенсионный план с установленными взносами
256	degeneracy	упадок, вырождение
257	demand	спрос
258	demise	передача недвижимости
259	demonstrably commited	формально обязанный
260	demutualization	утрата взаимного статуса
261	dent	выемка
262	depreciable amount	амортизируемая сумма
263	depreciable assets	амортизируемые активы
264	depreciation	амортизация
265	depreciation schedule	схема начисления амортизации
266	depression of trade	депрессия в торговле
267	derecognition	прекращение признания, списание с баланса
268	derivative	производная функция
269	derivative financial instrument	производные финансовые инструменты, деривативы
270	detection risk	риск необнаружения
271	developed reserves	освоенные (разработанные) запасы
272	development	разработка
273	development costs	затраты на разработку
274	development risk	риск развития страхового случая (в страховании)
275	development well	эксплуатационная скважина
276	deviation	отклонение
277	device	проект, устройство
278	diagram	диаграмма
279	dichotomy	дихотомия
280	differentiation	дифференциация
281	diluted earnings per share	разводненная прибыль на акцию
282	diluted loss per share	разводненный убыток на акцию
283	dilutive potential ordinary shares	потенциальные обыкновенные акции с разводняющим эффектом
284	dimand	требование, запрос
285	diminish	уменьшать, сокращать
286	diminishing balance method	метод убывающего остатка
287	diminishing returns	сокращающиеся доходы
288	direct acquisition cost	прямые затраты на приобретение
289	disbursement	расплата
290	disclaimer of opinion	отказ от выражения мнения
291	disclosure	раскрытие информации
292	discontinued operation	прекращенная деятельностьоперация
293	discount rate	дисконтная ставка
294	discovery	открытие (месторождения)
295	disposal of subsidiary	продажа дочерней компании
296	disposal proceeds	поступления от выбытия (активов)
297	distribution	распределение, распространение
298	diversification	диверсификация
299	diversified common stock fund	диверсифицированный фонд, инвестирующий в обыкновенные акции
300	dividend	дивиденды
301	divisible surplus	подлежащий распределению остаток
302	dollar-cost averaging	инвестирование фиксированных сумм
303	double declining method	метод двойного уменьшаемого остатка
304	downward adjustment	понижение цены
305	dowry	пособие
306	draft	переводной вексель
307	drain	расход, убыль
308	driblet	небольшая сумма
309	dry goods	мануфактура, галантерея
310	duality	двойственность
311	duopoly	дуополия
312	duty-paid	оплаченный пошлиной
313	earnest	задаток, залог
314	earnings	фактический доход
315	economic benefits	экономические выгоды
316	economic entity	экономическая организация
317	economic life	период эффективного использования
318	economy	хозяйство, экономия, бережливость
319	effective interest method	метод эффективной ставки процента
320	effective interest rate	эффективная ставка процента
321	effective tax rate	фактическая налоговая ставка
322	effectiveness	эффективность
323	efficiency	продуктивность, производительность
324	elasticity	эластичность
325	embargo	эмбарго
326	emergency funds	резервные фонды
327	emission	эмиссия
328	empirical	эмпирический
329	employ	применять
330	endow	обеспечивать постоянным доходом
331	engagement letter	письмо-обязательство
332	engagement objective	цель аудиторского задания
333	enterprise	предприятие
334	entity-specific measurement	специфическая оценка
335	entry	проводка
336	environmental risk	риск, связанный с окружающей средой
337	equal	уравнение
338	equality	равенство
339	equalization reserves	резервы колебаний убыточности
340	equation	уравнение, выравнивание
341	equilibrium	равновесие
342	equipment	оборудование
343	equity	обыкновенная акция
344	equity compensation plan	план компенсационных выплат долевыми инструментами
345	equity funds	фонды, специализирующиеся на акциях
346	equity instrument	долевой инструмент учета по долевому участию
347	equity method	метод долевого участия
348	equivalent	эквивалент
349	escess	излишек
350	estate	имущество
351	estate of policy holder	наследуемое имущество страхователя
352	estimate	смета, оценка
353	estimation sampling	оценочная выборка
354	event	событие
355	evidence	основание, свидетельство
356	examination	проверка
357	excess	превышение, избыток, излишек
358	excess capacity	избыток мощностей
359	excess of loss reinsurance	перестрахование эсцедента убытков
360	exchange	обмен, менять, биржа
361	exchange difference	курсовая разница
362	exchange rate	обменный курс
363	exogenous	экзогенный (внешний)
364	expand	расширять
365	expected disposals of assets	ожидаемое выбытие активов
366	expences	расходы
367	expenditure	затраты, расходы
368	expenses	расходы
369	expensive	дорогой
370	experience adjustments	корректировки на основе опыта
371	expert	эксперт
372	explanatory note	пояснительная записка
373	explicit	точный, определенный
374	exploitation	эксплуатация
375	exploration permit	разрешение на поисково-разведочные работы
376	exploratory well	разведочная скважина
377	export credit	экспортный кредит
378	exposure	подвергать риску
379	extensions	прирост запасов в результате доразведки
380	extensive	обширный экстенсивный
381	external service production	сторонняя организация по оказанию услуг
382	extraordinary items	результаты чрезвычайных обстоятельств
383	extraordinary profit	прибыль от чрезвычайных обстоятельств
384	fair presentation	объективное представление
385	faire value	справедливая стоимость
386	faithful representation	правдивое (достоверное) представление
387	feasible soluiton	альтернативное решение
388	fee	гонорар, плата, взнос
389	field work	работа на местах, вне штаб-квартиры фирмы
390	fifo method	метод фифо (первый - приход, первый - выбытие)
391	figure	цифра, арифметика
392	finance	финансировать
393	financial asset	финансовые активы
394	financial instrument	финансовый инструмент
395	financial liability	финансовые обязательства
396	financial position	финансовое положение
397	financial statements	финансовые отчеты
398	financing	финансирование
399	financing activities	финансовая деятельность
400	firm	фирма, предприятие
401	firm commitment	твердое соглашение, твердое обязательство
402	fiscal period	налоговый период
403	fixed asset	основное средство
404	fixed costs	постоянные затраты
405	fixed price contract	договор с фиксированной ценой
406	fixed production overheads	постоянные накладные производственные расходы
407	foreign currency	иностранная валюта
408	foreign currency transactions	операции с иностранной валютой
409	foreign entity	зарубежное предприятие
410	foreign operation	зарубежная деятельность
411	forfeit	конфискация
412	forgivable loans	условно-безвозвратные займы
413	forwarder	экспедитор
414	free enterprise	свободное предпринимательство
415	freight	фрахт, стоимость перевозки
416	freight costs on purchases	стоимость транспортировки при покупке
417	freight-in	транспортные расходы (фрахт) при покупке
418	freight-out	транспортные расходы (фрахт) при продаже
419	full cost accounting	метод учета по полным затратам
420	fully depreciated asset	полностью самортизированный актив
421	fund	капитал, фонды
422	fundamental errors	фундаментальные ошибки
423	fundholder	владелец финансовых фондов
424	funding	отчисление в пенсионный фондфондирование
425	funding	финансирование
426	funds held for customer	средства, которые компания держит для клиента
427	furnish	снабжать
428	future economic benefit	будущая экономическая выгода
429	gains	доходы от неосновной деятельности
430	gamble	спекулировать
431	game theory	теория игр
432	general disclosure	основные требования к раскрытию информации
433	general insurance	общее страхование
434	general standard	общий стандарт
435	geographical segment	географический сегмент
436	global/local maximum	глобальный, локальный максимум
437	going concern	непрерывность деятельности
438	goods	товар, имущество
439	goodwill	деловая репутация
440	governance	управление
441	governance process	процесс управления
442	government assistance	государственная помощь
443	government grants	правительственная субсидия
444	grade	степень, ранг
445	grant	дотация
446	grant related to assets	субсидия, относящаяся к активам
447	grant related to income	субсидия, относящаяся к доходу
448	grasp	контроль
449	gross investment in the lease	валовые инвестиции в аренду
450	guaranteed residual value	гарантированная остаточная стоимость
451	handsel	залог, задаток
452	hedge effectiveness	эффективность хеджирования
453	hindrance	преграда, препятствие
454	hire-purchase contract	договор аренды с правом выкупа
455	historical cost	первоначальная фактическая стоимость приобретения
456	historical cost accounting	учет по первоначальной стоимости
457	historical quarterly returns	историческая квартальная доходность
458	holding	владение
459	homogeneity	однородность, гомогенность
460	hop	скачок
461	host	множество
462	host bond	основная облигация
463	host contract	основной договор
464	hurdle rate	минимальная ставка доходности (используемая в той или иной организации)
465	hypothesis	гипотеза
466	ibnr (incurred but not reported)	резерв произошедших, но незаявленных убытков (рпну)
467	identity	тождественность
468	illuminate	изображать
469	immaterial (item)	несущественная (статья)
470	impairment loss	убыток от снижения стоимости
471	imparity principle	учет в соответствии с принципом обесценивания
472	import	импорт, импортировать
473	improved recovery projects	проекты для повышения отдачи
474	imputed rate of interest	инкриминиро-ванная ставка процента
475	inaccurancy	неточность, ошибка
476	inception of the lease	начало срока аренды
477	incidence	сфера действия, сфера распределения, охват
478	incidence of taxation	налоговое бремя
479	inclination	отклонение
480	income	доход
481	income distributions to owners	распределение прибыли (дохода) между собственниками
482	income statement	отчет о прибылях и убытках
483	income tax	подоходный налог
484	income tax expense	расходы по налогу на прибыль
485	incoming auditor	новый аудитор
486	incorporated enterprise	акционерная фирма
487	incorrect rejection	ошибочное отклонение (непринятие)
488	increase	увеличивать, повышать
489	increment	прибыль, рост, приращение
490	incremental sale	продажа с платежом в рассрочку
491	incur	потерпеть убытки
492	indemnity reinsurance	перестрахование возмещения ущерба
493	independence	независимость
494	independent foreign operation	независимая зарубежная деятельность
495	indepted	в долгу
496	index	индекс, показатель
497	indifference	безразличие
498	indifference map	карта безразличий
499	individual evaluation concept	принцип индивидуальной оценки
500	industry	промышленность, индустрия
501	industry segments	отраслевые сегменты
502	inferred mineral resources	предварительно оцененные запасы
503	inflation	инфляция
504	inherent limitation	неотъемлемое ограничение
505	inherent risk	неотъемлемый риск
506	initial disclosure event	событие первоначального признания
507	initial investment	первоначальные инвестиции
508	input	затраты, расходы
509	inscribed	вписанный
510	instalment	очередной взнос
511	instalment sale	продажа в рассрочку
512	insurable interest	страховой интерес
513	insurance expenses	расходы на страхование
514	insured event	страховой случай (застрахованное событие)
515	intangible asset	нематериальный актив
516	integer programming	целочисленное программирование
517	integrity	целостность
518	interchange	обмен, чередование
519	interest	интерес, выгода, проценты,
520	interest expense	расходы на выплату процентов
521	interest rate implicit in a lease	ставка процента, подразумеваемая в договоре об аренде
522	interim financial report	промежуточный финансовый отчет
523	interim period	промежуточный период
524	interior maximum	внутренний максимум
525	internal audit department	отдел внутреннего аудита
526	internal control system	система внутреннего контроля
527	interpret	объяснять, толковать
528	intersection	пересечение
529	inventories	запасы
530	inventory	инвентаризация, опись, инвентарь
531	investee	объект инвестиций
532	investigation	исследование
533	investing activities	инвестиционная деятельность
534	investment	инвестирование, вложение средств
535	investment object	объект инвестирования
536	investment property	инвестиционная собственность
537	investment securities	инвестиционные ценные бумаги
538	investor in a joint venture	инвестор в совместную деятельность
539	invoice	счет-фактура
540	joint control	совместный контроль
541	joint venture	совместная деятельность
542	jointly controlled entity	совместно контролируемая компания
543	just-in-time	точно в срок
544	labor	труд, работа
545	lease term	срок аренды
546	legal obligation	юридическое обязательство
547	legal right of set-off	юридическое право на зачет требований
548	leverage	леверидж, экономический рычаг
549	liability method	метод обязательств
550	lifo method	метод лифо (последний-поступление, первый - выбытие)
551	likelihood	вероятность
552	limit	предел
553	liquid	ликвидный
554	liquidity	ликвидность
555	liquidity risk	риск ликвидности
556	living	средства к жизни
557	lopside	односторонний
558	loss	убыток
559	loss on sale of equipment	убыток от продажи оборудования
560	lower	низкий, снижать
561	magnitude	величина, размер
562	main product	основная продукция
563	management	управление, менеджмент
564	management efficiency	эффективность управления
565	management fee	комиссия за управление
566	management of change	управление изменениями
567	manufacture	производство
568	marginal	предельный, маржинальный, крайний
569	markdown	понижающая составляющая нормы прибыли, скидка
570	market	рынок
571	market risk	рыночный риск
572	market value	рыночная стоимость
573	marketable (adj)	рыночный
574	marketing	маркетинг
575	mark-up	повышать цену
576	matching of costs with revenues	соотнесение затрат и выручки
577	material misstatement of fact	существенное искажение факта
578	material weaknesses	существенные недостатки
579	materiality level	уровень существенности
580	mathematical expression	математическое выражение
581	matrix	матрица
582	maximize	максимизировать
583	measure	мера, масштаб
584	measure of capacity	мера объема
585	measured reliably	надежно оцененный
586	measurement	оценка, измерение
587	mention	Упоминание, ссылка
588	merchandise inventory	товарные запасы
589	merchandising company	торговая компания
590	merger	Слияние
591	mineral rights (interests)	права на разработку недр
592	minerals in place	полезные ископаемые в недрах
593	minimum lease payments	минимальные арендные платежи
594	mitigating	уменьшение (компенсация влияния фактора)
595	monopoly	монополия
596	monopsony	монопсония
597	mortality protection	страхование на случай смерти
598	multiplicity	разнообразие, множество
599	multiply	умножать
600	net current assets	чистые текущие активы
601	net investment in a lease	чистые инвестиции в аренду
602	net profit	чистая прибыль
603	net purchases	чистые покупки
604	no entry	операция не отражается
605	non-cash item	неденежная статья
606	notation	система обозначения
607	notes payable	счета к оплате
608	notes to the accounts	пояснения к отчетности
609	notional amount	условная сумма
610	numerator	числитель
611	objective	цель, объект
612	obligating event	обязывающее событие
613	obligation	обязательство
614	obsolescence	моральный износ
615	occurrence risk	риск частоты страховых случаев
616	offset	возмещать
617	oligopoly	олигополия
618	open-end funds	открытые инвестиционные фонды
619	opening balance	начальное сальдо
620	operating activity	операционная деятельность
621	operating income	операционный доход
622	operating profit	операционная прибыль
623	operations-research investigation	исследование операций
624	opinion	мнение
625	optimal	оптимальный
626	option	опцион
627	option to acquire acreage	опцион на приобретение участка недр
628	ordinary activities	обычная деятельность
629	ordinary share common stock	обыкновенная акция
630	ore body	рудное тело
631	originated loans and receivables	сумма выданных займов и дебиторской задолженности
632	outlay	издержки
633	outpayments	выплата
634	output	выпуск, продукция, выход продукции, объем производства
635	overhead costs	накладные расходы
636	overlift (overtake, overproduction)	перепроизводство
637	owner-occupied property	объект недвижимости, занимаемый собственником
638	paid-in сapital	оплаченный капитал
639	par value	номинальная стоимость, паритет
640	parent company	материнская компания
641	partner (of an audit company)	партнер (аудиторской фирмы)
642	passively managed funds	пассивно управляемые фонды
643	past service cost	стоимость прошлых услуг работников
644	pay out	выплачивать
645	payments	платежи
646	payoff	выплата, компенсация
647	pecuniary	денежный, облагать штрафом
648	pension plan settlement	расчет по пенсионному плану
649	percent rank in category	процентный ранг в категории
650	percentage	процент, процентное отношение
651	performance	результаты деятельности
652	performance statement	отчет о результатах деятельности
653	performer	исполнитель
654	periodic system	система периодического учета
655	permanent difference	постоянная разница
656	perspective financial information	прогнозная финансовая информация
657	persuasive	убедительный
658	pivot	точка опоры, точка вращения
659	planning	планирование
660	plant	завод, фабрика
661	plenty	избыток
662	policyholder	страхователь, застрахованное лицо
663	possession	владение, обладание
664	potential ordinary share	потенциальные обыкновенные акции
665	predecessor	предшественник
666	predecessor auditor	предшествующий аудитор
667	preference	предпочтение
668	premise	предпосылка
669	prepaid expenses	расходы будущих периодов
670	prepayment	предоплата
671	presence	наличие
672	presentation	представление (информации)
673	presentation and disclosure	представление и раскрытие информации
674	price risk	ценовой риск
675	price-leadership	лидерство в ценах
676	pricing	ценообразование
677	private enterprise	частное предприятие
678	proceed	выручка, доход
679	produce	производить
680	product	продукт
681	production cost	производственная себестоимость
682	productive capacity	производственная мощность
683	professional services	профессиональные услуги
684	profit	прибыль, доход
685	profit and loss account	счет прибылей и убытков
686	projection	прогнозирование
687	proof	доказательство
688	proportionate consolidation	пропорциональное сведение
689	proprietor	владелец
690	prospecting permit	разрешение на изыскательские работы
691	prove	доказывать
692	provide	обеспечивать, продвигать
693	provision	резерв
694	purchacer	покупатель
695	purchase	покупка
696	purchase account	счет покупок
697	purchase discounts	скидки при покупке
698	purchase method	метод покупки
699	purchase price	цена покупки
700	pure competition	чистая конкуренция
701	pure monopoly	чистая монополия
702	purpose	намерение, цель
703	qualitative	качественный
704	quantity	количество, размер, величина
705	quotient	частное, коэффициент
706	range	ряд, линия, цепь
707	rate	облагать налогом, оценивать
708	ratio estimation	оценочное значение коэффициента
709	raw materials	сырьё
710	real earnings	реальные доходы
711	realised / unrealised gain	реализованная/нереализованная прибыль
712	reaudit	повторный аудит
713	recapitulate	перечислять, суммировать
714	recognition and measurement	признание и оценка
715	recompletion	переоборудование скважины
716	recording	отражение в учете, запись
717	redemption	погашение, выкуп
718	redemption fee	комиссия за изъятие средств
719	refuse to recognize	отказаться от признания
720	reinsurance premium	перестраховочная премия
721	reinsurer	перестраховщик
722	related parties	связанные стороны
723	related services	сопутствующие услуги
724	relative loss	относительные издержки
725	relative price	относительная цена
726	release	выпуск
727	remainder	остаток
728	remuneration	заработная плата, вознаграждение
729	rent	арендная плата
730	rent expense	расходы на аренду
731	reserves	фонды (резервы)
732	residual claim on total assets	остаточная доля в активах
733	residual value (salvage value)	ликвидационная стоимость
734	residue	остаток
735	resource	ресурс
736	restatement	пересчет
737	restructuring	реструктуризация
738	retail method	метод учета по розничным ценам
739	retailer	розничный торговец
740	retained earnings	нераспределенная прибыль
741	retirement benefit plan	пенсионный план
742	retirements	списание (основных средств)
743	retrospective application	ретроспективное применение
744	return	доход, прибыль, оборот, возврат
745	revaluation	переоценка
746	revenue	годовой доход
747	reverse acquisition	обратная покупка
748	revise	проверка, ревизия
749	rival	конкурент, соперник
750	sacrificeable	жертвовать, в убыток
751	salaries expense	расходы на оплату труда
752	salary	жалованье
753	sales	продажи
754	sales charge	комиссия за продажу
755	sales discounts	скидки при продаже
756	sales force	стимулирование продаж
757	sales forecast	прогноз сбыта
758	sales of goods and services	продажа товаров и услуг
759	sample size	размер выборки
760	savings	сбережения
761	scale	масштаб, размер
762	scarce	скудный, недостаточный
763	scope	сфера деятельности
764	scope of an audit	объем аудита
765	second request	повторный запрос
766	section	секция
767	securities held for resale	ценные бумаги для перепродажи
768	segment	сегмент, отрезок
769	segment expense	расходы сегмента
770	segment result	результат сегмента
771	seller	продавец
772	sequence	последовательность
773	settlement value	стоимость погашения
774	severance tax	налог на добытые полезные ископаемые
775	severity risk	риск размера страхового возмещения
776	shade	незначительное количество
777	share premium	премия на акцию, эмиссионный доход
778	shareholders' equity (interests)	собственный капитал
779	shipment	груз, партия
780	side condition	пограничное условие
781	slope	наклон
782	small entity	малое предприятие
783	solve	решать, платежеспособный
784	solvency	платежеспособность
785	special purpose auditor's report	отчет аудитора по специальному заданию
786	speculation	спекуляция
787	squeeze	взвинчивание цен, ограничение
788	stable	устойчивый
789	standard cost	нормативная себестоимость, затраты
790	standard deviation	среднее квадратическое отклонение
791	statistical sampling	статистическая выборка
792	statistics	статистика
793	stock	инвентарь, запас, сырьё, основной капитал
794	stock market game	игра на бирже
795	stockholder	акционер
796	storage equipment	складское оборудование
797	store	запас
798	stratification	стратификация
799	subsequent event	последующее событие
800	subsequent investment	последующие инвестиции
801	subsidy	дотация
802	substantive procedure	процедура проверки по существу
803	substitiute products	товар-заменитель
804	substitution	подстановка
805	substruct	извлекать
806	sufficiently	достаточное количество
807	sum	сумма
808	supervision	надзор
809	supplier	поставщик
810	supplies	материалы
811	supply	предожение
812	supply depot	торговая база
813	supply function	функция предложения
814	surface	поверхность
815	surmise	предположение, догадка
816	tangent	тангенс
817	tantamount	равносильный
818	tariff	тариф
819	tax	налог
820	tax allocation	распределение налогов
821	tax expense	расходы по налогу
822	tax liability	обязательства по налогам
823	tax loss	налоговый убыток
824	tax on income	налог на прибыль
825	tax rate	налоговая ставка
826	taxable profit	налогооблагаемая прибыль
827	tend	иметь тенденцию
828	tenure	срок пребывания в должности
829	term	термин, условия
830	term life insurance	страхование жизни на срок
831	tests of control	тесты контроля
832	theorem	теорема
833	time horizon	временной горизонт
834	timeliness	своевременность
835	title insurance	титульное страхование
836	title to assets	право собственности на активы
837	tool	инструмент
838	total return	общая (совокупная) доходность
839	trade	торговля, ремесло
840	trade-price	оптовая цена
841	trading house	торговый дом
842	trading securities	торговые ценные бумаги
843	transaction	сделка
844	transfer agent	трансфертный агент
845	treasury stock	собственные выкупленные акции (доли)
846	treat	трактовка
847	trial balance	пробный (проверочный) баланс
848	triangle	треугольник
849	trust activities	операции доверительного управления
850	turn out	выпускать
851	turnover	оборот
852	turnover ratio	коэффициент оборачиваемости активов
853	uncertainty	неопределенность
854	underdeveloped	слабо развитый
855	underlift (undertake)	недостаточная добыча (недобор)
856	underlying	основообразующий
857	understandability	понятность
858	undersupply	избыточное производство
859	undertake	брать на себя определенные обязательства
860	undeveloped reserves	неосвоенные запасы
861	undivided interest	неделимое долевое участие
862	unearned finance income	незаработанный финансовый доход
863	unearned revenue	незаработанные доходы (доходы будущих периодов)
864	unexpired risk	неистекший риск
865	unfunded benefit plan	нефондированный пенсионный план
866	unguaranteed residual value	негарантированная ликвидационная стоимость
867	union	объединение, союз
868	unit	единица измерения
869	unit cost	себестоимость единицы продукции
870	uniting of interests	объединение интересов
871	units and goods available	общее количество товаров
872	units of activity	объем продукции
873	unproved reserves	недоказанные запасы
874	untenable	устойчивый
875	upper-case	преобладающая ситуация
876	useful life	срок полезного использования
877	utility	полезность
878	valid	действительный
879	value at risk	стоимость, подверженная риску
880	variable costs	переменные затраты
881	venturer	участник (совместной деятельности)
882	viability	жизнеспособность
883	volume	объем, емкость
884	wage-rate	ставка, тариф заработной платы
885	wages	заработная плата
886	warehouse	склад
887	wares	товары
888	warranty expense	расходы по гарантийному обслуживанию
889	waste	расточительство, трата
890	wealth	богатство, изобилие
891	weighted average cost	средневзвешенная стоимость
892	welfare	благосостояние
893	work in progress	незавершенное производство
894	working capital	оборотные средства
895	working papers	рабочие документы
896	worth	цена, стоимость
897	write-off	списание
898	write-up	повышение стоимости
899	yearly term reinsurance	перестрахование на годичный срок
900	yield	доходность

4. Сочинение «Моя будущая научная работа»

My future scientific work

I want to tell you about my future scientific work. My speciality is called as informatic-economist I got in the Kama Polytechnical Institute in 2003. This speciality is connected with information technologies, with aim of which enterprises can obtain their high results and realize their aims.

My future scientific work is related with methods of increase of the economic and management’s efficiency. I suppose that it can be obtained on the basis of the informatic-analytic system of the enterprise. Here suppose the informatic-analytic system must not be constructed by the functional criteria. I think to increase the economic and management’s efficiency it is necessary to design firm’s system on the basis of the business-processes. Then the enterprise is aggregate of interconnected business-processes. Besides for increase of the economic and management’s efficiency firm must use a well-elaborated mathematic apparatus. This apparatus contains many of mathematic models and methods, which in total let to optimize the activity of enterprise.

In this work I am assisted by my scientific supervisor. His name is Smirnov Yuri Nicolaevich. He is the head of our Chair “The mathematic model-building and information technologies in economics”. With him I and my group mates took part in some All-Russian conferences, where we sent our reports on economics and information technologies. One of my reports called “The mathematic model-building of marketing”. In this work I described possible mathematic methods and models with aim of which the firm can optimize all its marketing activities. Our materials were published in the scientific collections of articles in many towns of our country.

Besides there is a scientific seminar in our Chair. Its title is “The synergetic economics”. There we do reports on this theme and discuss the got results.

In future I suppose to work in our Chair as a teacher on mathematic model-building and operations research in economics. Now I work with first- and third-year students in this direction. I want to prolong my scientific investigations in this sphere. Our collective is high-qualified. Here many clever and interesting people work. They help us in our investigations.

5. Библиография

William J. Baumol. Economics theory and operations analysis, third edition.

Объём переведенного текста с языка оригинала – 600 тыс. печатных знаков (с. 318-575).